![]() 上海罗店中学第一学期期中测试
上海罗店中学第一学期期中测试
高中一年级数学
2017.11
1、填空题(每小题3分,共36分)
1、已知集合![]() ,
,![]() ,则
,则![]() =__________
=__________
2、已知集合![]() ,
,![]() ,若
,若![]() ,则实数
,则实数![]() =______
=______
3、不等式![]() 的解集为
的解集为![]() ,则
,则![]() =________
=________
4、不等式![]() 的解集为_________
的解集为_________
5、若![]() ,则满足条件的集合
,则满足条件的集合![]() 的个数为_______
的个数为_______
6、若不等式![]() 的解集中的整数有且仅有1、2、3,则实数
的解集中的整数有且仅有1、2、3,则实数![]() 的取值范围为_________
的取值范围为_________
7、若不等式![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是________
的取值范围是________
8、试写出![]() 的一个充要条件____________
的一个充要条件____________
9、已知![]() ,且满足
,且满足![]() ,则
,则![]() 的取值范围是__________
的取值范围是__________
10、若不等式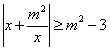 对所有非零实数
对所有非零实数![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是___________
的取值范围是___________
11、若![]() ,且
,且![]() ,
,![]() ,则
,则![]() 的取值范围是________
的取值范围是________
12、对于实数![]() 概念运算“
概念运算“![]() ”:
”: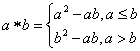 ,设
,设![]() ,且关于
,且关于![]() 的方程
的方程![]() 恰有三个互不相等的实数根
恰有三个互不相等的实数根![]() ,则
,则![]() 的取值范围是________
的取值范围是________
2、选择题(每小题4分,共16分)
13、设命题甲:![]() ;命题乙:
;命题乙:![]() ,则命题甲是命题乙的( )
,则命题甲是命题乙的( )
A、充分非必要条件
B、必要非充分条件
C、充要条件
D、既非充分又非必要条件
14、不等式![]() 的解集是( )
的解集是( )
A、![]()
B、![]()
C、![]()
D、![]()
15、若正数![]() 满足
满足![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
A、![]()
B、![]()
C、![]()
D、![]()
16、在![]() 上概念运算
上概念运算![]() :
:![]() ,若不等式
,若不等式![]() 对任意实数
对任意实数![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是( )
的取值范围是( )
A、![]()
B、![]()
C、![]()
D、![]()
3、解答卷(8分+8分+10分+10分+12分=48分)
17、解不等式组: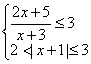
18、若不等式![]() 对任意实数
对任意实数![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围
的取值范围
19、某工厂拟建一座平面图形为矩形且面积为200平米的三级污水处置池。矩形的长为![]() 米,假如池四周围墙建造单价为400元/米,中间两道隔墙建造单价为248元/米,池底建造单价为80元/米2,水池所有墙的厚度忽视不计。试设计污水处置池的长和宽,使总造价最低,并求出最低总造价?
米,假如池四周围墙建造单价为400元/米,中间两道隔墙建造单价为248元/米,池底建造单价为80元/米2,水池所有墙的厚度忽视不计。试设计污水处置池的长和宽,使总造价最低,并求出最低总造价?
![]()
![]()

![]()
![]()
20、已知![]() ,
,![]() ,
,![]() ,求
,求![]()
21、已知,![]() ,问是不是存在实数
,问是不是存在实数![]() ,使得不等式
,使得不等式![]() 对所有实数
对所有实数![]() 恒成立。若成立,求出所有
恒成立。若成立,求出所有![]() 的值;若没有,说明理由
的值;若没有,说明理由







