天山二中2017学年第一学期初三数学期中考试题
1、选择题（本大题共6小题，每小题4分，满分24分）
1．下列命题中不正确的是…………………………………………………………（ ▲ ）
（A）等边三角形都是相似图形； （B）矩形都是相似图形；
（C）正方形都是相似图形； （D）圆心角相等的扇形都是相似图形
2. 已知
，下列说法中，错误的是…………………………………………（ ▲ ）
（A）
（B）
（C）
（D）
3. DABC中，ÐC=90°，AC=1，BC=2，则∠B的余切值为…………………………（ ▲ ）
（A）
（B）
（C）2 （D）
4. 下列各组条件中，肯定能推得△ABC与△DEF一样的是………………………（ ▲ ）
（A）∠A=∠E且∠D=∠F； （B）∠A=∠B且∠D=∠F；
（C）∠A=∠E且
； （D）∠A=∠E且
．
5. 如图，MN∥PQ，
，
，那样满足
的图形是………………（ ▲ ）
6. 已知C是直线AB上一点，且
，那样下列结论中，正确的是……（ ▲ ）
（A）
（B）
（C）
（D）
二．填空题：（本大题共12小题，每小题4分，满分48分）
7. 已知线段b是线段a、c的比率中项，且a=4、b=9那样c=__________.
8. 化简：
=__________.
9. 假如两个相似三角形的面积比是1：4，那样它们的周长比为____________________.
10. 已知AD是△ABC的中线，点G是△ABC的重点，
，那样用向量
表示向量
为__________.
11. 如图，已知D、E分别是△ABC的边AB、AC上的点，DE∥BC，且DE:BC=3:5，则AD:BD=________________.
12. 某人想通过光的反射原理测量古城墙CD高度，设计在地面P处放一平面镜，当手电筒光线从点A处出发，经平面镜反射后刚好照射到城墙顶端C处，已知AB⊥BD，CD⊥BD，AB=1.2米，PB=1.8米，PD=4.8米，那样城墙CD高=__________米.
13． 已知点M是线段AB的黄金分割点（AM＞MB），假如AM＝
cm，那样AB＝__________cm.
14. 直角三角形ABC中，∠A=90°，正方形EFGH的四个顶点在三角形的边上，如图，已知BE=6，FC=2，则正方形EFGH的面积是__________.
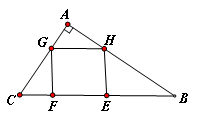
（第12题图）
15. 如图，在梯形ABCD中，AD∥BC，AC与BD相交于点O，假如AD:BC=2:3，那样=__________．
16. 如图，直线AA1∥BB1∥CC1，假如
，
，
，那样线段BB1的长是_______________________．
17. 已知在
中，
，
，
，点D是射线BC上的一点（不与端点B重合），联结AD，假如△
与△
相似，那样BD=______________．
18．如图，在△ABC中，AC=BC=2，∠C=900，点D为腰BC中点，点E在底边AB上，且DE则BE的长为_________.
3、简答卷：（本大题共7题，满分78分）
19．（本题满分10分）
计算：
20.
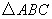如图，矩形ABCD中，AB=3，AD=5，点E在AD上，且AE:ED=1:4，联结BE，射线EF⊥BE交边DC于点F. 求CF的长.
21. （本题满分10分，其中第1小题4分，第2小题6分 ）
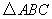已知，如图，点E、F、G分别在AB、AC、AD上，且EG∥BD，FG∥CD，
，四边形BCFE的面积比三角形AEF的面积大17，
（1）求证：EF∥BC；
（2）求△ABC的面积.
22．（本题满分10分，其中第1小题4分，第2小题6分）
如图，在梯形ABCD中，AB∥CD，且AB:CD=4:3，E是CD的中点，AC与BE交于点F.
（1）求
的值；
（2）若
，请用
来表示.
23. （本题满分12分，其中第1小题6分，第2小题6分）
已知：如图，在△中，，
，中线BE和AD交于点F．
求：（1）△ABC的面积；（2）
的值．
24.（本题满分12分，其中第1小题4分，第2小题8分）
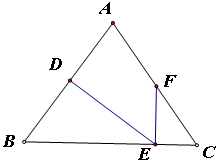在△ABC中，AB=AC=5，BC=6，点D在边AB上，DE
AB.点E在边BC上, 点F在边AC上，且∠DEF=∠B .
求证：△FCE∽△EBD；
当点D在线段AB上运动时，是不是大概使S△FCE=4S△EBD，假如大概求出BD的长，假如不可能,请说明理由.
25.（本题满分14分，其中第1小题4分，第2小题6分，第3小题4分）
在中，
，,，是边
上一动点（不与端点、重合），过动点的直线l与射线相交于点，与射线BC相交于点F，
（1）设
，点在边上，与相似，求此时的长度．
（2）假如点E在边AB上，以点E、B、F为顶点的三角形与以点E、A、D为顶点的三角形相似，设CD＝x，BF＝y，求y与x之间的函数分析式并写出函数的概念域．
（3）设，以点E、B、F为顶点的三角形与以点E、A、D为顶点的三角形相似，
求的值．（直接写出答案）
天山二中2017学年第一学期初三数学期中考试评分标准
1、B。 2、C 3、C 4、C 5、A 6、A
7、 8、
9、
10、、
11、 12、3.2 13、1 14、12
15、 16、3 17、7或25 32 18、
19、解：原式=+-----------------5分
=-----------------2分+2分
=2-1-----------------1分
20、 解：∵AE:ED=1:4，AD=5, ∴AE=1，ED=4, -----------------2分
∵矩形ABCD，∴∠A=∠D=90°，∴∠AEB+∠ABE=90°
∵EF⊥BE，∴∠AEB+∠DEF=90°, ∴∠ABE=∠DEF,
∴△ABE∽△DEF，-----------------------------------3分
∴
,-----------------------------------1分
∴,∴----------------------------2分
∴
，-----------------------------2分
21、证明
∵EG∥BD∴-----------------------------------1分
∵FG∥CD∴
-----------------------------------1分
∴-----------------------------------1分
∴EF∥BC-----------------------------------1分
∵EF∥BC
∴△AEF∽△ABC-----------------------------------1分
∴S△AEF:S△ABC=2-----------------------------------1分
又∵
∴=-----------------------------------2分
∴S△AEF =4-----------------------------------1分
∴S△ABC=25-----------------------------------1分
22、 解：（1）∵AB∶CD=4∶3，E是CD的中点，
∴AB∶CE=8∶3，--------------------------------------（2分）
又∵AB‖CD，
∴.---------------------------------（2分）
∵AB‖CD，AB∶CD=4∶3，
，
∴，-------------------------------------（2分）
∴
，----------------------（1分）
又，则，----------------------（2分）
∴.----------------------（1分）
23、解：∵△中，
，且AD是中线,∴AD⊥BC,.-----（2分）
∵Rt△中，，，
∴----------------------------------------------------------------（2分）
∴
，∴S△ABC=60. -----------------------（2分）
∵中线BE和AD交于点F, ∴-----------------------------------------（2 分）
则在Rt△BDF中，
-----------------------（2 分）
∴-----------------------------------------------------------（2分）
24、
25．解：由勾股定理得：
.--------------------------------------------------------（1分）
∵过动点的直线l与射线BC相交于点F，即DE不平行于BC，
∴只可能DE⊥AB，即△ADE∽△ABC---------------------（1分）
由，解得
， ----------------------------------------（1分）
∴
. --------------------------------------------------------（1分）
过点的直线l交线段于点，交的延长线于点
，
∵
，，
假如与相似，那样只能.
又∵，∴.-------------------------------（3分）
∴
. ∴．
∴．--------------------------------------------------------（3分）
当直线l交线段于点，交的延长线于点时，
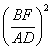＝＝．--------------------------------------------------------（2分）
当直线l交线段的延长线于点、
交线段BC于点F时，
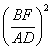＝＝．--------------------------------------------------------（2分）
的值等于或．（答案直接得分）
