2017学年第一学期姚连生中学初中三年级数学期中考试题
(完卷时间:
100分钟,满分:
150分)
1、选择题:(本大题共6题,每题4分,满分24分)
1.东海大桥全长32.5千米,假如东海大桥在某张地图上的长为6.5厘米,那样该地图上距离与实质距离的比为………………………………………………………………( ).
A.1:5000000; B.1:500000; C.1:50000; D.1:5000.
2.假如两个相似三角形对应高之比是9∶16,那样它们的对应周长之比是 ……( ).
A.3∶4; B.4∶3; C.9∶16; D.16∶9.
3.Rt△ABC中,∠C=90º,若AC=a,∠A=![]() ,则AB的长为……………………( ).
,则AB的长为……………………( ).
A.![]() ; B.
; B.![]() ; C.
; C.![]() ; D.
; D.![]() .
.
4、下列说法中正确的有 ………………………………………………………… ( )
三边对应成比率的两个三角形相似;
两边对应成比率且一个角对应相等的两个三角形相似;
一个锐角对应相等的两个直角三角形相似;
对应角分别相等的两个四边形相似.
1个; 2个; 3个; 4个.
5.已知非零向量![]() 、
、![]() 和
和![]() ,下列条件中,不可以断定
,下列条件中,不可以断定![]() ∥
∥![]() 的是 …………( )
的是 …………( )
(A)![]() ∥
∥![]() ,
,![]() ∥
∥![]() ; (B)
; (B)![]() =
=![]() ,
,![]() =
=![]() ;
;
(C)![]() =
=![]() ; (D)
; (D)![]() .
.
6.已知D是△ABC的BC上的一点,∠BAD=∠C,那样下列正确的是( )
(A)![]() ; (B)
; (B)![]() ;
;
(C)![]() ; (D)
; (D)![]() .
.
2、填空题(本大题共12题,每题4分,满分48分)
7.若![]() ,则
,则![]() __________.
__________.
8.若将抛物线y=-3x2+2向上平移2个单位,则平移后抛物线的分析式__________.
9.计算:![]() __________.
__________.
10. 已知点P是线段AB上的黄金分割点,且AP>BP,AB=4cm,则线段AP=__________cm.
11. 某一时刻,身高1.6米的小明在阳光下的影长是0.2米,同一时刻同一地址测得某旗杆的影长是3米,那样旗杆的高度是__________米.
12. 已知在△ABC中,点G是三角形的重点,则![]() __________
__________
13.如图,在□ABCD中,点![]() 在
在![]() 边上,若
边上,若![]() ,则
,则![]() 的值为__________.
的值为__________.
14.在△ABC中,假如![]() ,
,![]() ,那样BC的长__________.
,那样BC的长__________.
15.某山路的路面坡度为![]() ,若沿此山路向上前进90米,则升高了__________米.
,若沿此山路向上前进90米,则升高了__________米.
16. 若某抛物线图像的顶点在原点,且经过点(-2,1),则此抛物线的分析式是__________.
17.如图,在△ABC中,D是AC边上一点,且![]() ,设
,设![]() ,
,![]() ,假如用向量
,假如用向量![]() ,
,![]() 表示向量
表示向量![]() ,那样
,那样![]() __________.
__________.
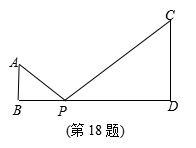
![]()
 如图,AB⊥BD,CD⊥BD,AB=6,CD=16,BD=20,一动点P从点B向点D运动,若△PAB与△PCD是相似三角形,则BP的值是__________.
如图,AB⊥BD,CD⊥BD,AB=6,CD=16,BD=20,一动点P从点B向点D运动,若△PAB与△PCD是相似三角形,则BP的值是__________.
3、简答卷(本大题共5题,19~22题每题10分,23题12分,满分52分)
![]() 19.计算:
19.计算:
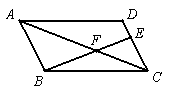
20. 如图,已知点D、E分别在△ABC的边AB和AC上,DE//BC,![]() ,四边形DBCE的面积为16.
,四边形DBCE的面积为16.
(1)求△ABC的面积;
(2)假如向量![]() ,
,![]() ,请用
,请用![]() 、
、![]() 表示向量
表示向量![]() =__________.
=__________.
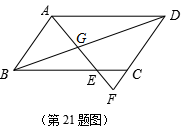 21.如图,已知在平行四边形ABCD中,点E在边BC上,射线AE交BD于点G,交DC的延长线于点F,AB=6,BE=3EC,求DF的长.
21.如图,已知在平行四边形ABCD中,点E在边BC上,射线AE交BD于点G,交DC的延长线于点F,AB=6,BE=3EC,求DF的长.
22.如图是一座大楼前的六级台阶的截面图,每级台阶的高为0.15米,宽为0.30米,现要将它改为无障碍通道(图中EF所示的斜坡),假如斜坡EF的坡角为8º,求斜坡底部点F与台阶底部点A的距离AF.(精准到0.01米)
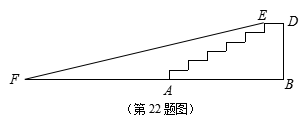 (备用数据:tan8º=0.140,sin8º=0.139,cosplay8º=0.990)
(备用数据:tan8º=0.140,sin8º=0.139,cosplay8º=0.990)
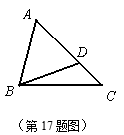
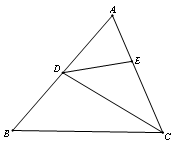 23、已知,如图,在△ABC中,CD平分∠ACB,点E在AC上,
23、已知,如图,在△ABC中,CD平分∠ACB,点E在AC上,![]()
(1)找出图中的相似三角形,并证明;
(2)若AD=6,AE=4,DE=![]() ,求BD的长
,求BD的长
4、综合题(24题12分,25题14分,合计26分)
24、如图,等腰三角形ABC中,AB=AC,![]() ,
,
 (1)证明:
(1)证明: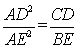
 当
当![]() ,求证
,求证![]()
(3)当![]() ,猜想BC、BE、CD的数目关系,不必证明.
,猜想BC、BE、CD的数目关系,不必证明.
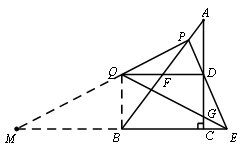
seline;"=""> 25.如图,在△ABC中,∠ACB=90°,AC=8,![]() ,D为边AC 中点,P为边AB上一点 ,直线PD交BC延长线于点E,设线段BP长为
,D为边AC 中点,P为边AB上一点 ,直线PD交BC延长线于点E,设线段BP长为![]() ,线段CE长为
,线段CE长为![]() .
.
seline;"=""> (1)求![]() 关于
关于![]() 的函数分析式并写出概念域;
的函数分析式并写出概念域;
seline;"=""> (2)过点D作BC平行线交AB于点F,在DF延长线上取一点 Q,使得QF=DF,
seline;"=""> 联结PQ、QE,QE交边AC于点G,
seline;"=""> 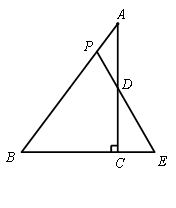 ①当△EDQ与△EGD相似时,求
①当△EDQ与△EGD相似时,求![]() 的值;
的值;
seline;"=""> ②求证:![]() .
.
seline;"="">
seline;"="">
学年第一学期姚连生中学初中三年级数学期中考试题期中答案
1、B 2、C 3、D 4、B 5.D; 6.B.
7、![]() 8、y=-3x2+4 9、
8、y=-3x2+4 9、![]() 10、
10、![]() 11、24 12、
11、24 12、![]()
13、![]() 14、12 15、10 16、
14、12 15、10 16、![]() 17、
17、![]()
18、![]() ,8, 12(漏解0分)
,8, 12(漏解0分)
19、![]()
20)解:(1)![]()
![]()
![]() (1分)
(1分)
![]() DE//BC
DE//BC
![]() ∽
∽![]() (1分)
(1分) ![]() (1分)
(1分)
设![]() ,则
,则![]() (1分)
(1分)
![]()
![]() (1分)
(1分)
![]()
![]() (1分)
(1分)
(2)![]() (答案2分,过程2分)
(答案2分,过程2分)
21、解:在平行四边形ABCD中,AB=CD………………………………(2分)
∵AB∥CD,∴![]() .……………………………………………………(3分)
.……………………………………………………(3分)
又∵BE=3EC,AB=6,∴CF=2.………………………………………………(3分)
∵CD=AB=6,∴DF=8.…………………………………………………………(2分)
22.解:作EH⊥AB,垂足为点H.………………………………………………………(2分)
由题意,得EH=0.9,AH=1.5.…………………………………………………(2分)
在Rt△EFH中,![]() ,∴
,∴![]() .………………………………(2分)
.………………………………(2分)
∴FH≈6.429.……………………………………………………………………(1分)
∴AF=FH-AH=6.429-1.5=4.929≈4.93(米).…………………………………(2分)
答句………………………………………………………………………………………………………(1分)
23. (1)△CDE∽△CBD…………(1分)
等积式化比率式…………(1分)
角平分线…………(1分)
SAS…………(1分)
△ADE∽△ACD…………(1分)
一线二等角…………(1分)
∠A公共角…………(1分)
AA…………(1分)
(2)AC=9…………(1分)
CE=5…………(1分)
DC=8…………(1分)
BD=218/15…………(1分)
24.A.A…………(1分)
同理A.A…………(1分)
△EAB∽△DCA…………(1分)
面积比=相似比平方…………(1分)
面积比=同高底边比…………(1分)
得证…………(1分)
(2)BC²/2=AB²…………(2分)
一样的比率式…………(1分)
得证…………(1分)
(3)BC²=3BE·CD…………(2分)
25. 解:(1)在Rt△ACB中,![]() ,
,![]() ,
,![]() .……………………(1分)
.……………………(1分)
过点P作PH⊥BE,垂足为H. ………………………………………………(1分)
在Rt△PHB中,![]() ,
,![]() .(1分)
.(1分)
∵CD∥HP,∴![]() ,即
,即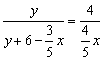 .
.
解得![]() . ……………………………………………… (2分)
. ……………………………………………… (2分)
(2)联结QB,∵DQ=BC=6,DQ∥BC,
∴四边形QBCD是平行四边形. ∴BQ=4.
又∵∠ACB=90°,∴∠EBQ =90°. ………………………………… ………………(1分)
当△EDQ与△EGD相似时,∵∠EDG <∠EDQ∴∠EDC =∠DQE.
∵DQ∥CE,∴∠DQE =∠QEB,∴∠EDC =∠QEB .
又∵∠EBQ=∠DCE=90°∴△EBQ ∽△DCE . …………………………………(1分)
∴![]() ,即
,即![]() ,解得
,解得![]() (舍)
(舍)![]() . ………………………(1分)
. ………………………(1分)
 代入
代入![]() , 得
, 得![]() . …………………………………………………………(1分)
. …………………………………………………………(1分)
(3)延长PQ,交EB延长线于M. …………(1分)
∵DQ∥ME,∴![]() .
.
又∵![]() ,∴MB=BE. …………………(1分)
,∴MB=BE. …………………(1分)
又由①得QB⊥ME, …………………(1分)
∴QE=QM. …………………………………(1分)
∵DQ∥ME,∴![]() .
.
又∵QE=QM,∴![]() .即
.即![]() . …………………………(1分)
. …………………………(1分)
双向细目表及得分率一览
班级 | 题型 | 考试知识点 | 1班 | 2班 | 3班 | 4班 | 年级 |
1 | 选择 | 24.2(1)比率尺 | 0.71 | 0.59 | 0.8 | 0.81 | 0.73 |
2 | 选择 | 24.5(3)相似三角形的性质 | 0.92 | 0.73 | 0.95 | 0.96 | 0.89 |
3 | 选择 | 25.1(2)锐角三角比的意义 | 0.75 | 0.64 | 0.95 | 0.85 | 0.8 |
4 | 选择 | 24.4(3)相似三角形的断定 | 0.42 | 0.41 | 0.5 | 0.44 | 0.44 |
5 | 选择 | 24.6(2)向量与实数相乘 | 0.67 | 0.41 | 0.95 | 0.7 | 0.68 |
6 | 选择 | 24.4相似三角形断定、24.5相似三角形性质 | 0.58 | 0.36 | 0.85 | 0.7 | 0.62 |
选择 | 0.67 | 0.52 | 0.83 | 0.75 | 0.69 | ||
7 | 填空 | 24.2(1)比率线段 | 1 | 0.91 | 1 | 1 | 0.98 |
8 | 填空 | 26.2(2)特殊二次函数的图像、平移 | 0.88 | 0.82 | 0.95 | 0.96 | 0.9 |
9 | 填空 | 24.7(1)向量的线性运算 | 0.88 | 0.59 | 0.9 | 0.96 | 0.84 |
10 | 填空 | 24.2(2)比率线段、黄金分割 | 0.63 | 0.59 | 0.95 | 0.96 | 0.78 |
11 | 填空 | 24.5(2)相似三角形的性质 | 0.71 | 0.68 | 0.85 | 0.89 | 0.78 |
12 | 填空 | 24.3(2)三角形一边的平行线、重心 | 0.54 | 0.41 | 0.65 | 0.63 | 0.56 |
13 | 填空 | 24.3(1)三角形一边的平行线的性质 | 0.71 | 0.55 | 0.9 | 0.93 | 0.77 |
14 | 填空 | 25.4(2)解直角三角形的应用 | 0.67 | 0.32 | 0.85 | 0.85 | 0.68 |
15 | 填空 | 25.4(1)解直角三角形的应用、坡度 | 0.54 | 0.05 | 0.55 | 0.7 | 0.47 |
16 | 填空 | 26.2(1)特殊二次函数的图像 | 0.38 | 0.27 | 0.75 | 0.96 | 0.6 |
17 | 填空 | 24.7(2)向量的线性运算 | 0.5 | 0.18 | 0.8 | 0.59 | 0.52 |
18 | 填空 | 24.5(4)相似三角形的性质 | 0.33 | 0.23 | 0.65 | 0.48 | 0.42 |
填空 | 0.65 | 0.47 | 0.82 | 0.83 | 0.69 | ||
19 | 简答 | 25.2(1)求锐角三角比的值 | 0.65 | 0.44 | 0.93 | 0.87 | 0.72 |
20 | 简答 | 24.5(3)相似三角形性质24.7向量的线性运算 | 0.56 | 0.33 | 0.8 | 0.69 | 0.6 |
21 | 简答 | 24.5(1)相似三角形的性质 | 0.7 | 0.56 | 0.96 | 0.93 | 0.79 |
22 | 简答 | 25.4(4)解直角三角形的应用 | 0.52 | 0.26 | 0.83 | 0.75 | 0.59 |
23 | 简答 | 24.3相似三角形的性质24.4相似三角的断定 | 0.53 | 0.34 | 0.68 | 0.76 | 0.59 |
简答 | 0.59 | 0.38 | 0.83 | 0.8 | 0.65 | ||
24 | 综合 | 24.3相似三角形的性质24.4相似三角的断定 | 0.26 | 0.13 | 0.45 | 0.5 | 0.34 |
25 | 综合 | 综合题 | 0.08 | 0.03 | 0.18 | 0.23 | 0.14 |
综合 | 0.17 | 0.08 | 0.31 | 0.35 | 0.23 | ||
平均分 |
|
| 82.2 | 56.9 | 110 | 108 | 89.9 |
去双外 |
|
| 100 | 67.5 | 113 | 109 | 100 |







