23.2 解直角三角形及其应用
1、选择题（共5题）
1．在△ABC中，∠C=90°，a=5，c=13，用科学计算器求∠A约等于（ ）
A．24°38′ B．65°22′ C．67°23′ D．22°37′
2．在△ABC中，∠C=90°，a，b，c分别是∠A，∠B，∠C的对边，有下列关系式：①b=ccosplayB，②b=atanB，③a=csinA，④a=bcotB，其中正确的有（ ）
A．1个 B．2个 C．3个 D．4个
3．为测一河两岸相对两电线杆A、B间距离，在距A点15m的C处，（AC⊥AB），测得∠ACB=50°，则A、B间的距离应为m
A．15sin50° B．15cosplay50° C．15tan50° D．15cot50°
4．如图，在Rt△ABC中，∠C＝90°，∠A＝30°，E为AB上一点且AE∶EB＝4∶1，EF⊥AC于F，连接FB，则tan∠CFB的值等于．
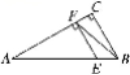
A． 
B． 
C． 
D．
5．如图，在等腰Rt△ABC中，∠C＝90°，AC＝6，D是AC上一点，若tan∠DBA＝ 
，则AD的长为．
A．2 B． 
C． 
D．1
2、填空题（共4题）
6．如图，孔明同学背着一桶水，从山脚A出发，沿与地面成30°角的山坡向上走，送水到山上因今年春天受旱缺水的王奶奶家，AB＝80米，则孔明从A到B上升的高度BC是__________米．
7．将一副三角尺如图所示叠放在一块，若AB＝14 cm，则阴影部分的面积是______ cm2.
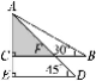
8．如图，在Rt△ABC中，∠CAB＝90°，AD是∠CAB的平分线，tan B＝ 
，则CD∶DB＝__________.
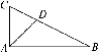
9．如图，在△ABC中，∠B＝45°，cosplay C＝ 
，AC＝5a，则△ABC的面积用含a的式子表示为________．
3、计算与解答卷（共2题）
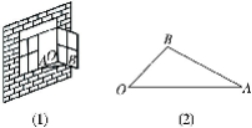
10．如图，在平面直角坐标系内，O为原点，点A的坐标为，点B在第一象限内，BO＝5，sin∠BOA＝ .
求：点B的坐标；cosplay∠BAO的值．
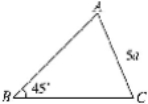
11．如图，在△ABC中， AD是BC上的高，tan B＝cosplay∠DAC．
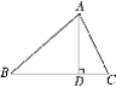
求证：AC＝BD；
若sin C＝ 
，BC＝12，求9．图是图中窗子开到肯定地方时的平面图，若∠AOB＝45°，∠OAB＝30°，OA＝60 cm，求点B到OA边的距离．
参考答案
1．D
2．C
3．C
4.分析：设EB＝1，则AE＝4，BC＝ 
，AC＝ 
.
∴CF＝ 
.
∴tan∠CFB＝ .
答案：C
5.A
6.分析：如图，过点D作DE⊥AB，垂足为E.易证△ADE为等腰直角三角形，AE=DE.在Rt△BDE中，tan∠DBA= 
，所以BE=5AE.在等腰Rt△ABC中，∠C=90°，AC=6，由勾股定理可求出AB= 
，所以AE= .在等腰Rt△ADE中，由勾股定理可求出AD的长为2.
7.40
8.分析：Rt△ABC中，AB＝14 cm，∠B＝30°，则AC＝7 cm，
易知CF＝AC＝7 cm，
所以阴影部分的面积为 
cm2.
答案：
9.分析：过D作DE⊥AB于点E.
∵tan B＝ ，∴DE＝ 
．
∵∠CAB＝90°，AD是∠CAB的平分线，
∴∠DAE＝45°.∴∠ADE＝45°.
∴∠DAE＝∠ADE.∴AE＝DE.
∵DE∥CA，∴CD∶DB＝AE∶EB＝1∶2.
答案：
1∶2
10.解：如图，作BH⊥OA，垂足为H.
在Rt△OHB中，∵BO＝5，sin∠BOA＝ ，
∴BH＝BO·sin∠BOA＝3.∴OH＝4.
∴点B的坐标为．
∵OA＝10，OH＝4，∴AH＝6.
在Rt△AHB中，BH＝3，
∴AB＝ 
.
∴cosplay∠BAO＝ .
AD的长．
11.证明：∵AD⊥BC，
∴△ABD和△ADC为直角三角形．
∴tan B＝ 
，cosplay∠DAC＝ 
.
∵tan B＝cosplay∠DAC，
∴ ＝ ，即AC＝BD．
解：在Rt△ADC中，已知sin C＝ ＝ ，
故可设AD＝12k，AC＝13k.
∴CD＝ 
＝5k.
∵BC＝BD＋CD，又AC＝BD，
∴BC＝13k＋5k＝18k.
由已知BC＝12，
∴18k＝12.
∴k＝ 
.∴AD＝12k＝8.
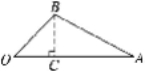
13.解：如图，过点B作BC⊥OA于点C，∵∠AOB=45°，
∴∠CBO=45°，
BC=OC．
设BC=OC=x，∵∠OAB=30°，
∴AC= 
.
∵OC+CA=OA，
∴x+ =60．
∴x= 
≈22，
即点B到OA边的距离是22 cm.
