2018-2019学年上海交大附中第二学期
高中二年级数学3月数学月考试题
1、填空题
1、复数
（
是虚数单位）的模是____________.
2、在如图所示的正方体
中，异面直线
与
所成角的大小为________.
3、已知点
，则与
方向相同的单位向量的坐标为________.
4、已知双曲线
，则以双曲线的焦点为顶点，以双曲线顶点为焦点的椭圆方程为____.
5、已知两圆
和
相交于
两点，则直线
的方程是__________.
6、将参数方程
（
为参数）化为普通方程，所得方程是_______________.
7、已知椭圆
的焦距为，则实数
_________.
8、已知
是实系数一元二次方程
的两根，则
的值为_________.
9、若
为非零实数，则下列四个命题者成立：①
；②；③若
，则
；④若
，则
则对于任意非零复数，上述命题仍然成立的序号是_____________.
10、如图，
是三角形所在平面外的一点，
，且
，
、
分别是和的中点，则异面直线
与
所成角的大小为_______________（用反三角函数表示）
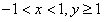
11、已知直线
及平面
，其中
，那样在平面内到两条直线距离相等的点的集合可能是：①一条直线；②一个平面；③一个点；④空集.其中正确的是____________.
12、动点
在角坐标系平面上能完成下为时伟，先从原点
沿正偏北方向行走一段时间后，再向正北方向行走，但何时改变方向不定，假定速度为10米/分钟，则当变化时行走2分钟内的可能落点的地区面积是_______________.
2、选择题
13、在下列命题中，不是公理的是（ ）
A、平行于同一个平面的两个平面相互平行
B、过不在同一条直线上的三点，有且只有一个平面
C、假如同一条直线上的两点在同一个平面内，那样这条直线上所有些点都在此平面内
D、假如两个不重合的平面有一个公共点，那样他们有且只有一条过该点的公共直线
14、若空间三条直线
满足
，则直线
与
（ ）
A、肯定平行 B、肯定相交 C、肯定是异面直线 D、肯定垂直
15、在四边形中，，则四边形的面积为（ ）
A、 B、 C、5 D、10
16、已知动点的横坐标
、纵坐标满足：①
；②，那样当变化时，点形成的图形的面积为（ ）
A、 B、 C、
D、
3、解答卷
17、如图，是正方形，直线底面
，是
的中点.
（1）证明：直线
平面
；
（2）求直线与平面所成角的正切值.
18、已知椭圆的焦点为
为椭圆上一点，且是
，的等差中项.
（1）求椭圆方程；
（2）假如点在第二象限且
，求
的值.
19、已知平面与平面的交线为直线为平面内一条直线；
为平面一条直线，且直线
互不重合.
（1）若直线与直线交于点，判断点与直线的地方关系并证明；
（2）若，判断直线与直线的地方关系并证明.
20、现代城市大多是棋盘式布局（如北京道路几乎都是东西和南北走向）.在这种城市中，大家说的两点间的距离总是不是指两点间的直线距离（位移），而是实质路程（如图）.在直角坐标平面内，大家概念两点间的“直角距离”为：
.
（1）在平面直角坐标系中，写出所有满足到原点的“直角距离”为2的“格点”的坐标.（格点指横、纵坐标均为整数的点）
（2）求到两定点
、的“直角距离”和为定值
的动点轨迹方程，并在直角坐标系内作出该动点的轨迹.（在以下三个条件中任选一个做答，多做不计分，基保选择条件①，满分3分；条件②满分4分；条件③，满分6分）
①；
②
；
③.
（3）写出同时满足以下两个条件的“格点”的坐标，并说明理由（格点指横、纵坐标均为整数的点）.
①到两点“直角距离”相等；
②到
两点“直角距离”和最小.
参考答案：
1、填空题：
1、； 2、
； 3、； ；4； 5、； 6、；
7、
； 8、1； 9、②④； 10、； 11、（1）（2）（4）； 12、；
2、选择题：
13、A；14、D；15、C；16、B；
3、解答卷：
17、（1）证明略；（2）；
18、（1）；（2）；
19、（1），证明略；（2），证明略；
20、分析：
解：（1）、
、、
、、、、
（2）条件①：轨迹方程为：
①当时，
；
②当时，；
③当时，；
④当时，
；
⑤当时，
；
⑥当时，.
条件②：轨迹方程为
①当时，
；
②当时，；
③当时，；
由对称性可得其他部分图形.
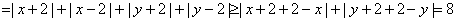
条件③：轨迹方程为：
①当时，
；
②当时，；
③当时，
；
由对称性可得其他部分图形.
（3）如图：满足条件的格点有、、、、、、
对于①，设满足到
、两点“直角距离”相等，
即满足，可得：（如图）
对于②，设到、
两点“直角距离”和最小，
即
当且仅当且等号成立.
可得，点.（如图）
故，同时满足条件①、②的格点的坐标是：、、、、、、、、.
21、（1），
；（2）；（3），；
