2019-2020学年上海风华初级九上周测
1、选择题
1. 下列说法中，正确的是（ ）
A. 所有矩形都相似 B. 所有些直角三角形都相似
C. 有一角是100°的所有等腰三角形都相似 D. 有一个角是50°的所有等腰三角形都相似
2. 假如
，那样等于（ ）
A. 
B. 
C. 
D. 
3. 下列线段中
，成比率线段的是（ ）
A. 
B. 
C. 
D. 
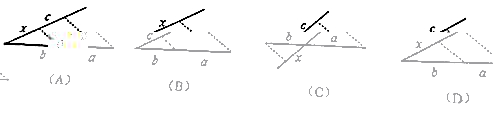
4. 下列推理中正确的是（ ）
A. 在图甲中，若
，则
//
//
B. 在图乙中，若
，则DE//BC
C. 在图丙中，若
，则AB//DE D. 在图丙中，若，则AB//DE
5. 已知线段
，求作线段
，使
，以下作法正确的是（ ）
6. 已知
的三边长分别为6cm、7.5cm、9cm，
的一边长为4cm，当的另两边长是下列哪一组时，这两个三角形相似（ ）
A. 2cm、3cm B. 4cm、5cm C. 5cm、6cm D. 6cm、7cm
2、填空题
7.已知线段成比率，其中
，则d=____________cm
8. 已知
，则____________
9. 一个四边形的边长分别是3、4、5、6，另一个与它一样的四边形最小边长为6，则另一个四边形的周长是____________
10. 已知线段AB的黄金分割点为P，其中较长线段AP=6厘米，则原线段AB=____________，较短线段PB=____________
11. 在等腰三角形ABC中，腰AC=5厘米，底BC=8厘米，G是三角形ABC的重点，则线段AG=____________
厘米
12. 一个直角三角形的两边长分别为3和6，另一个直角三角形的两边长分别为2和4，那样这两个直角三角形____________相似（填“肯定”、“未必”或“肯定不”）
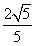
13. 如图，在平行四边形ABCD中，AB=12cm，AD=5cm，E为AD的中点，在AB上取一点F，使
，则AF=____________cm
14. 如图，正方形ABCD的边长为2，AB=EB，MN=1，线段MN的两端分别在CB、CD上滑动，那样当CM=____________时，与
相似
15. 如图，在梯形ABCD中，AD//BC，两腰BA与CD的延长线相交于P，PF⊥BC，AD=3，BC=7，EF=4，则PF=____________
16. 如图，FG//DE//BC，且AG:GE:EC=1:2:3，那样FG:DE:BC=____________
17. 如图，在Rt中，∠A=90°，AB=6，AC=8，P是BC边上一点，作PE⊥AB于E，作PD⊥AC于D，设，则PD+PE=____________
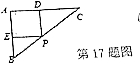
18. 在中，AB>BC>AC，D是AC的中点，过点D作直线L，使截得的三角形与原三角形相似，如此的直线L有____________条
3、解答卷
19. 已知线段a、b、c，求线段，使
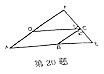
20. 如图，已知四边形ABCD是平行四边形，FC=54cm，CE=27cm，BE=32cm，求CD的长
21. 如图，已知中，D是BC上一点，BD=10，DC=8，∠DAC=∠B，E为AB上一点，DE//AC，求AC和DE的长
22. 如图所示，点E是正方形ABCD的边AB的中点，EF⊥ED交BC于点F，联结DF，求证：
23. 如图，已知，在锐角中，CE⊥AB于点E，点D在边AC上，联结BD交CE于点F，且
.
（1）求证：BD⊥AC；
（2）联结AF，求证：
.
24. 概念：若一个三角形一条边的平方等于另两条边的乘积，大家把这个三角形叫做比率三角形.
（1）已知是比率三角形，AB=2，BC=3，请直接写出所有满足条件的AC的长；
（2）如图1，在四边形ABCD中，AD//BC，对角线BD平分∠ABC，∠BAC=∠ADC，求证：是比
例三角形；
（3）如图2，在（2）的条件下，当∠ADC=90°时，求的值.
参考答案
1-6、CBCCBC
7、4 8、
9、36 10、
11、2
12、未必 13、 14、，
15、7
16、 18、4
19、略
20、64cm
21、，
22、证明略
23、证明略
24、（1）证明略；（2）证明略；（3）
