曹杨中学2018-2019学年第一学高中一年级期未数学模拟训练考试试题
1、填空题
1.已知集合
若
则实数
的取值范围是______.
2.若集合
且
则实数
_____.
3.已知
则
的最小值为______.
4.概念在R上的偶函数
在
止单调递增，则不等式
的解集是_________.
5.函数
的反函数是________.
6.若关于
的不等式
对
恒成立,则实数的取值范围为_______.
7.已知函数是奇函数,且当
时,
.若函数
是的反函数,则
_______.
8.若函数
在
上单调递增,那样实数的取值范围是_________.
9,函数的反函数为
假如函数的图像过点,那样函数
的图像肯定过点________.
10,若函数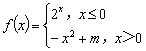
的值域为
则实数
的取值范围是________.
11.已知函数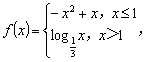
若对任意的
不等式恒成立,则实数的取值范围是________.
12.函数其中
若动直线
与函数的图像有三个不一样的交点,则实数的取值范围是____________.
2、选择题
13.已知
条件的解集为R；条件
则是的
A.充分非必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也非必要条件
14.下列函数在其概念域内既是奇函数又是增函数的是
A.
B. C. D.
15.小明在期中考后,想急迫地核对答案,于是他来到数学组办公室,探寻出卷的老师。此时办公室正好有四位老师,他们发现小明不认识他们中的任何一位,于是他们每个人说了一句话:
甲说:“我这学期还没有出过考试题呢！”
乙说：“丁出的这次考卷！”
丙说:“是乙出的试题！”
丁说:“出卷的不是我！”
他们告诉小明,只有一位老师说了谎话,而且出卷老师就在其中,那样请问到底是哪个出的期中试题
A.甲 B.乙 C.丙 D.丁
16.概念
为“取上整函数”，比如
以下关于“取上整函数”性质的描述,正确的是
①
②若则
③任意有
④
A①② B.①③ C.②③ D.②④
3、解答卷
17.
设函数
的概念域为集合A,函数的概念域为集合B.已知
满足
且是的充分条件,求实数的取值范围.
18.
已知函数
当时,求满足的的取值范围；
若的概念域为R,又是奇函数,求的分析式,判断其在R上的单调性并加以证明。
19.
已知二次函数的值域为
求出
的关系式,并判断此函数的奇偶性,请说明理由；
求出在上的最小值并求
的值域.
20.
某快递公司在某市的货物转运中心,拟引进智能机器人分拣系统,以提升分拣效率和减少物流本钱,已知购买台机器人的总本钱万元。
若使每台机器人的平均本钱最低,问应买多少台?
现按中的数目购买机器人,需要安排人将邮件放在机器人上,机器人将邮件送达指定落袋格口完成分拣,经实验知,每台机器人的日平均分拣量：
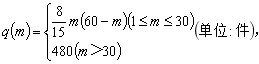
已知传统人工分拣每个人每天的平均分拣量为1200件,问引进机器人后,日平均分拣量达最大值时用人数目比引进机器人前的用人数目最多可降低百分之几?
21.
已知函数
在区间
上有最大值4和最小值1,设
求
的值；
若不等式在
有解,求实数
的取值范围；
若
有三个不一样的实数解,求实数的取值范围.
