2020-2021学年初二(上)月考数学试题
一.选择题(共10小题)
1.若长度分别为a,3,5的三条线段能组成一个三角形,则a的值可以是()
A.1 B.2 C.3 D.8
2.小华在电话中问小明:“已知一个三角形三边长分别是4,9,12,怎么样求这个三角形的面积?”小明提示说:“可通过作最长边上的高来求解.”小华依据小明的提示作出的图形正确的是()
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.已知如图,△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于()

A.315° B.270° C.180° D.135°
4.在△ABC中,已知∠A=3∠C=54°,则∠B的度数是()
A.90° B.94° C.98° D.108°
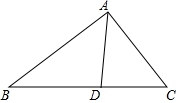
5.如图,BD,CE分别是△ABC的高线和角平分线,且相交与点O,若∠BCA=70°,则∠BOE的度数是()
A.60° B.55° C.50° D.40°
6.下列命题中真命题是()
A.若a2=b2,则a=b
B.4的平方根是±2
C.两个锐角之和肯定是钝角
D.相等的两个角是对顶角
7.如图,DE是△ABC的边AB的垂直平分线,D为垂足,DE交AC于点E,且AC=8,BC=5,则△BEC的周长是()
A.12 B.13 C.14 D.15
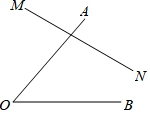
8.如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC.将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:依据仪器结构,可得△ABC≌△ADC,如此就有∠QAE=∠PAE.则说明这两个三角形全等的依据是()

A.SAS B.ASA C.AAS D.SSS
9.如图,已知∠ABC=∠DCB,添加以下条件,不可以断定△ABC≌△DCB的是()
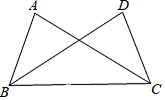
A.∠A=∠D B.∠ACB=∠DBC C.AC=DB D.AB=DC
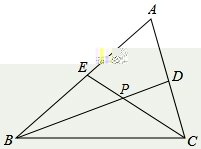
10.如图,在△ABC中,BD、CE分别是∠ABC和∠ACB的平分线,AM⊥CE于P,交BC于M,AN⊥BD于Q,交BC于N,∠BAC=110°,AB=6,AC=5,MN=2,结论①AP=MP;②BC=9;③∠MAN=35°;④AM=AN.其中不正确的有()
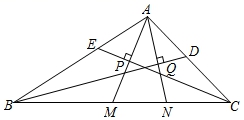
A.4个 B.3个 C.2个 D.1个
二.填空题(共10小题)
11.大家用如图的办法(斜钉上一块木条)来维修一条摇晃的凳子的数学原理是借助三角形的__________.
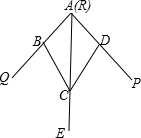
12.小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),你觉得将它中的哪一块带去,就能配一块与原来一样大小的三角形?应该带第__________块.
13.把命题“对顶角相等”改写成“假如…那样…”的形式:__________.
14.如图,点B、E、C、F在一条直线上,AB∥DE,AB=DE,BE=CF,AC=6,则DF=__________.
15.如图,△ABC≌△ADE,若∠C=35°,∠D=75°,∠DAC=25°,则∠BAD=__________°.
16.当三角形中一个内角α是另一个内角β的两倍时,大家称此三角形为“特点三角形”,其中α称为“特点角”.假如一个“特点三角形”的“特点角”为100°,那样这个“特点三角形”的最小内角的度数为__________.
17.如图所示,∠ACD是△BC的外角,∠A=45°,BE平分∠ABC,CE平分∠ACD,且BE、CE交于点E.∠E=__________.
18.如图,在△ABC中,∠C=90°,AC=BC,BD平分∠CBA交AC于点D,DE⊥AB于点E,且△DEA的周长为2019cm,则AB=__________.
19.如图,将△ABC纸片沿DE折叠,使点A落在点A′处,若∠A=33°,则∠1+∠2的度数是__________.
20.如图,D、E分别是△ABC边AB、BC上的点,AD=2BD,BE=CE,若S△ABC=18,设△ADF的面积为S1,△CEF的面积为S2,则S1﹣S2的值是__________.
三.解答卷(共3小题)
21.如图,AD平分∠BAC,其中∠B=35°,∠ADC=82°,求∠BAC,∠C的度数.
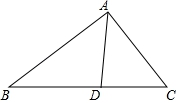
22.尺规作图:如图,在直线MN上求作一点P,使点P到∠AOB两边的距离相等(不需要写出作法,但要保留作图痕迹,写出结论)
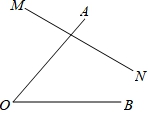
23.如图,AB=AD,AC=AE,∠BAE=∠DAC.求证:∠C=∠E.
24.如图,△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=5°,∠B=50°,求∠C的度数.

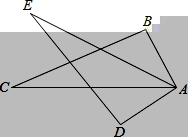
25.如图,CD是经过∠BCA顶点C的一条直线,且直线CD经过∠BCA的内部,点E,F在射线CD上,已知CA=CB且∠BEC=∠CFA=∠α.
(1)如图1,若∠BCA=80°,∠α=100°,问EF=BE﹣AF,成立吗?说明理由.
(2)将(1)中的已知条件改成∠BCA=∠β,∠α+∠β=180°(如图2),问EF=BE﹣AF仍成立吗?说明理由.
26.如图,在△ABC中,假如BD,CE分别是∠ABC,∠ACB的平分线且他们相交于点P,设∠A=n°.
(1)求∠BPC的度数(用含n的代数式表示),写出推理过程.
(2)当∠BPC=125°时,∠A=__________.
(3)当n=60°时,EB=7,BC=12,DC的长为____________________.
参考答案与考试试题分析
一.选择题(共10小题)
1.若长度分别为a,3,5的三条线段能组成一个三角形,则a的值可以是()
A.1 B.2 C.3 D.8
【剖析】依据三角形三边关系定理得出5﹣3<a<5+3,求出即可.
【解答】解:由三角形三边关系定理得:5﹣3<a<5+3,
即2<a<8,
即符合的只有3,
故选:C.
2.小华在电话中问小明:“已知一个三角形三边长分别是4,9,12,怎么样求这个三角形的面积?”小明提示说:“可通过作最长边上的高来求解.”小华依据小明的提示作出的图形正确的是()
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【剖析】由三角形的三边为4,9,12,可知该三角形为钝角三角形,其最长边上的高在三角形内部,即过最长边所对的角的顶点,作对边的垂线,垂足在最长边上.
【解答】解:∵42+92=97<122,
∴三角形为钝角三角形,
∴最长边上的高是过最长边所对的角的顶点,作对边的垂线,垂足在最长边上.
故选:C.
3.已知如图,△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于()
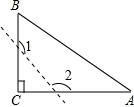
A.315° B.270° C.180° D.135°
【剖析】借助三角形内角与外角的关系:三角形的任一外角等于和它不相邻的两个内角之和解答.
【解答】解:∵∠1、∠2是△CDE的外角,
∴∠1=∠4+∠C,∠2=∠3+∠C,
即∠1+∠2=2∠C+(∠3+∠4),
∵∠3+∠4=180°﹣∠C=90°,
∴∠1+∠2=2×90°+90°=270°.
故选:B.
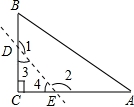
4.在△ABC中,已知∠A=3∠C=54°,则∠B的度数是()
A.90° B.94° C.98° D.108°
【剖析】依据题意得出∠C的度数,进而借助三角形内角和定理得出答案.
【解答】解:如图所示:∵∠A=3∠C=54°,
∴∠C=18°,
∴∠B的度数是:
180°﹣∠A﹣∠C=108°.
故选:D.

5.如图,BD,CE分别是△ABC的高线和角平分线,且相交与点O,若∠BCA=70°,则∠BOE的度数是()
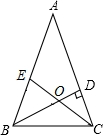
A.60° B.55° C.50° D.40°
【剖析】依据角平分线的概念和三角形的内角和即可得到结论.
【解答】解:∵BD⊥AC,
∴∠BDC=90°,
∵CE平分∠ACB,∠ACB=70°,
∴∠DCO=35°,
∴∠BOE=∠COD=90°﹣35°=55°,
故选:B.
6.下列命题中真命题是()
A.若a2=b2,则a=b
B.4的平方根是±2
C.两个锐角之和肯定是钝角
D.相等的两个角是对顶角
【剖析】借助平方根的概念对A、B进行判断;借助反例对C进行判断;依据对顶角的概念对D进行判断.
【解答】解:A、若a2=b2,则a=b或a=﹣b,所以A选项错误;
B、4的平方根是±2,所以B选项正确;
C、两个锐角之和可能不是钝角,若30°与60°的和为直角;所以C选项错误;
D、相等的两个角未必为对顶角,所以D选项错误.
故选:B.
7.如图,DE是△ABC的边AB的垂直平分线,D为垂足,DE交AC于点E,且AC=8,BC=5,则△BEC的周长是()
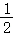
A.12 B.13 C.14 D.15
【剖析】直接借助线段垂直平分线的性质得出AE=BE,进而得出答案.
【解答】解:∵DE是△ABC的边AB的垂直平分线,
∴AE=BE,
∵AC=8,BC=5,
∴△BEC的周长是:BE+EC+BC=AE+EC+BC=AC+BC=13.
故选:B.
8.如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC.将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:依据仪器结构,可得△ABC≌△ADC,如此就有∠QAE=∠PAE.则说明这两个三角形全等的依据是()

A.SAS B.ASA C.AAS D.SSS
【剖析】在△ADC和△ABC中,因为AC为公共边,AB=AD,BC=DC,借助SSS定理可断定△ADC≌△ABC,进而得到∠DAC=∠BAC,即∠QAE=∠PAE.
【解答】解:在△ADC和△ABC中,
 ,
,
∴△ADC≌△ABC(SSS),
∴∠DAC=∠BAC,
即∠QAE=∠PAE.
故选:D.
9.如图,已知∠ABC=∠DCB,添加以下条件,不可以断定△ABC≌△DCB的是()

A.∠A=∠D B.∠ACB=∠DBC C.AC=DB D.AB=DC
【剖析】全等三角形的断定办法有SAS,ASA,AAS,SSS,依据定理逐个判断即可.
【解答】解:A、∠A=∠D,∠ABC=∠DCB,BC=BC,符合AAS,即能推出△ABC≌△DCB,故本选项错误;
B、∠ABC=∠DCB,BC=CB,∠ACB=∠DBC,符合ASA,即能推出△ABC≌△DCB,故本选项错误;
C、∠ABC=∠DCB,AC=BD,BC=BC,不符合全等三角形的断定定理,即不可以推出△ABC≌△DCB,故本选项正确;
D、AB=DC,∠ABC=∠DCB,BC=BC,符合SAS,即能推出△ABC≌△DCB,故本选项错误;
故选:C.
10.如图,在△ABC中,BD、CE分别是∠ABC和∠ACB的平分线,AM⊥CE于P,交BC于M,AN⊥BD于Q,交BC于N,∠BAC=110°,AB=6,AC=5,MN=2,结论①AP=MP;②BC=9;③∠MAN=35°;④AM=AN.其中不正确的有()

A.4个 B.3个 C.2个 D.1个
【剖析】①依据三角形的内角和定理断定∠CAM=∠CMA,由等腰三角形的断定和三线合一的性质可得结论正确;
②依据BN=AB=6,CM=AC=5,及线段的和与差可得BC的长;
③依据三角形的内角和定理及角的和与差可得结论;
④要想得到AM=AN,必有∠AMN=∠ANM,而AB≠AC,可知∠ABC≠∠ACB,从而得AM≠AN.
【解答】解:①∵CE平分∠ACE,
∴∠ACP=∠MCP,
∵AM⊥CE,
∴∠APC=∠MPC=90°,
∴∠CAM=∠CMA,
∴AC=CM,
∴AP=PM,
①正确;
②同理得:BN=AB=6,
∵CM=AC=5,
∴BC=BN+CM﹣MN=6+5﹣2=9,
②正确;
③∵∠BAC=∠MAC+∠BAN﹣∠MAN=110°,
由①知:∠CMA=∠CAM,∠BNA=∠BAN,
△AMN中,∠CMA+∠BNA=180°﹣∠MAN=∠BAN+∠MAC,
∴180°﹣∠MAN﹣∠MAN=110°,
∴∠MAN=35°,
③正确;
④当∠AMN=∠ANM时,AM=AN,
∵AB=6≠AC=5
∴∠ABC≠∠ACB,
∴∠AMN≠∠ANM,则AM与AN不相等,
④不正确;
所以本题不正确的有④,
故选:D.
二.填空题(共10小题)
11.大家用如图的办法(斜钉上一块木条)来维修一条摇晃的凳子的数学原理是借助三角形的__________.
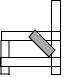
【剖析】当三角形三边的长度确定后,三角形的形状和大小就能唯一确定下来,故三角形具备稳定性,依据三角形具备稳定性回答即可.
【解答】解:用如图的办法(斜钉上一块木条)来维修一条摇晃的凳子的数学原理是借助三角形的稳定性,
故答案为:稳定性.
12.小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),你觉得将它中的哪一块带去,就能配一块与原来一样大小的三角形?应该带第__________块.
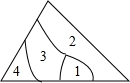
【剖析】本题应先假定选择哪块,再对应三角形全等断定的条件进行验证.
【解答】解:
1、3、4块玻璃不同时拥有包含一完整边在内的三个证明全等的要点,所以不可以带它们去,
只有第2块有完整的两角及夹边,符合ASA,满足题目需要的条件,是符合题意的.
故答案为:2.
13.把命题“对顶角相等”改写成“假如…那样…”的形式:__________.
【剖析】命题中的条件是两个角相等,放在“假如”的后面,结论是这两个角的补角相等,应放在“那样”的后面.
【解答】解:题设为:对顶角,结论为:相等,
故写成“假如…那样…”的形式是:假如两个角是对顶角,那样它们相等,
故答案为:假如两个角是对顶角,那样它们相等.
14.如图,点B、E、C、F在一条直线上,AB∥DE,AB=DE,BE=CF,AC=6,则DF=__________.

【剖析】依据题中条件由SAS可得△ABC≌△DEF,依据全等三角形的性质可得AC=DF=6.
【解答】证明:∵AB∥DE,
∴∠B=∠DEF
∵BE=CF,
∴BC=EF,
在△ABC和△DEF中,
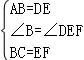 ,
,
∴△ABC≌△DEF(SAS),
∴AC=DF=6.
故答案是:6.
15.如图,△ABC≌△ADE,若∠C=35°,∠D=75°,∠DAC=25°,则∠BAD=__________°.
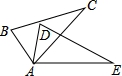
【剖析】依据全等三角形的对应角相等与三角形内角和定理,即可得到∠BAD的度数.
【解答】解:∵△ABC≌△ADE,∠D=75°,
∴∠D=∠B=75°,
又∵∠C=35°,
∴∠BAC=70°,
又∵∠DAC=25°,
∴∠BAD=45°,
故答案为:45.
16.当三角形中一个内角α是另一个内角β的两倍时,大家称此三角形为“特点三角形”,其中α称为“特点角”.假如一个“特点三角形”的“特点角”为100°,那样这个“特点三角形”的最小内角的度数为__________.
【剖析】依据已知一个内角α是另一个内角β的两倍得出β的度数,进而求出最小内角即可.
【解答】解:由题意得:α=2β,α=100°,则β=50°,
180°﹣100°﹣50°=30°,
故答案为:30°.
17.如图所示,∠ACD是△BC的外角,∠A=45°,BE平分∠ABC,CE平分∠ACD,且BE、CE交于点E.∠E=__________.
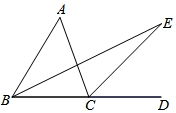
【剖析】先依据外角定理和∠A=45°,得出∠ACD﹣∠ABC=45°,再借助角平分线的概念得:![]() ∠ACD﹣
∠ACD﹣![]() ∠ABC=20°,即∠E=∠ECD﹣∠EBC=22.5°.
∠ABC=20°,即∠E=∠ECD﹣∠EBC=22.5°.
【解答】解:∵∠ACD是△ABC的一个外角,
∴∠ACD=∠A+∠ABC,
∴∠A=∠ACD﹣∠ABC,
∵∠A=45°,
∴∠ACD﹣∠ABC=45°,
∵BE平分∠ABC,CE平分∠ACD,
∴∠ECD=![]() ∠ACD,∠EBC=
∠ACD,∠EBC=![]() ∠ABC,
∠ABC,
∵∠ECD是△BCE的一个外角,
∴∠ECD=∠EBC+∠E,
∴∠E=∠ECD﹣∠EBC=![]() ∠ACD﹣
∠ACD﹣![]() ∠ABC=22.5°.
∠ABC=22.5°.
故答案为22.5°
18.如图,在△ABC中,∠C=90°,AC=BC,BD平分∠CBA交AC于点D,DE⊥AB于点E,且△DEA的周长为2019cm,则AB=______________________________.

【剖析】证明△BDC≌△BDE(AAS),再证明△ADE的周长=AB即可解决问题.
【解答】解:∵BD平分∠CBA,
∴∠CBD=∠ABD,
∵DE⊥AB,
∴∠ACD=∠BED=90°,
∵BD=BD,
∴△BDC≌△BDE(AAS),
∴BC=BE,DE=DC,
∵BC=AC,
∴AC=BE,
∵AD+AE+DE=AD+CD+AE=AC+AE=BE+AE=AB=2019(cm),
∴AB=2019(cm),
故答案为2019cm.
19.如图,将△ABC纸片沿DE折叠,使点A落在点A′处,若∠A=33°,则∠1+∠2的度数是__________.
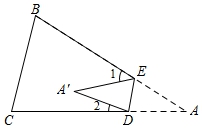
【剖析】证明∠1+∠2=2∠A即可解决问题.
【解答】解:连接AA′.
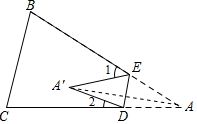
∵∠1=∠EA′A+∠EAA′,∠2=∠DA′A+∠DAA′,∠BCA=∠EA′D,
∴∠1+∠2=∠EA′A+∠EAA′+∠DA′A+∠DAA′=∠EAD+∠EA′D=2∠EAD=66°,
故答案为66°.
20.如图,D、E分别是△ABC边AB、BC上的点,AD=2BD,BE=CE,若S△ABC=18,设△ADF的面积为S1,△CEF的面积为S2,则S1﹣S2的值是__________.
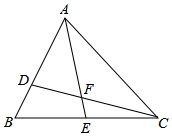
【剖析】依据D、E分别是△ABC边AB、BC上的点,AD=2BD,BE=CE,S△ABC=18,可以得到S△ADC和S△AEC的面积,再依据图形,即可得到S1﹣S2的值.
【解答】解:∵D、E分别是△ABC边AB、BC上的点,AD=2BD,BE=CE,S△ABC=18,
∴S△ADC=12,S△AEC=9,
∵S△ADC=S△ADF+S△AFC,S△AEC=S△CEF+S△AFC,
∴S△ADC﹣S△AEC=S△ADF﹣S△CEF,
∵S△ADC=12,S△AEC=9,
∴S△ADC﹣S△AEC=3,
∴S△ADF﹣S△CEF=3,
∵△ADF的面积为S1,△CEF的面积为S2,
∴S1﹣S2=3,
故答案为:3.
三.解答卷(共3小题)
21.如图,AD平分∠BAC,其中∠B=35°,∠ADC=82°,求∠BAC,∠C的度数.

【剖析】第一依据邻补角的常识求出∠ADB的度数,再依据三角形内角和定理求出∠BAD的度数,又依据角平分线的常识求出∠BAC的度数,最后第三借助三角形内角和定理求出∠C的度数.
【解答】解:∵∠ADC=82°,
∴∠ADB=180°﹣82°=98°,
∴∠BAD=180°﹣∠B﹣∠ADB=180°﹣35°﹣98°=47°,
∵AD平分∠BAC,
∴∠BAC=2∠BAD=2×46°=94°,
∴∠C=180°﹣35°﹣94°=51°.
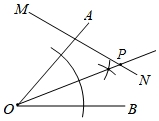
22.尺规作图:如图,在直线MN上求作一点P,使点P到∠AOB两边的距离相等(不需要写出作法,但要保留作图痕迹,写出结论)

【剖析】借助角平分线的作法作∠AOB的平分线,∠AOB的平分线与直线MN交于一点,这一点就是P点.
【解答】解:如图所示,作∠AOB的平分线,∠AOB的平分线与直线MN交于一点,则点P即为所求.
23.如图,AB=AD,AC=AE,∠BAE=∠DAC.求证:∠C=∠E.
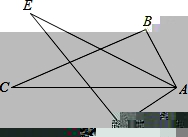
【剖析】由“SAS”可证△ABC≌△ADE,可得∠C=∠E.
【解答】证明:∵∠BAE=∠DAC
∴∠BAE+∠CAE=∠DAC+∠CAE
∴∠CAB=∠EAD,且AB=AD,AC=AE
∴△ABC≌△ADE(SAS)
∴∠C=∠E
24.如图,△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=5°,∠B=50°,求∠C的度数.

【考试知识点】K2:三角形的角平分线、中线和高.
【剖析】依据直角三角形两锐角互余求出∠AED,再依据三角形的一个外角等于与它不相邻的两个内角的和求出∠BAE,然后依据角平分线的概念求出∠BAC,再借助三角形的内角和定理列式计算即可得解.
【解答】解:∵AD是BC边上的高,∠EAD=5°,
∴∠AED=85°,
∵∠B=50°,
∴∠BAE=∠AED﹣∠B=85°﹣50°=35°,
∵AE是∠BAC的角平分线,
∴∠BAC=2∠BAE=70°,
∴∠C=180°﹣∠B﹣∠BAC=180°﹣50°﹣70°=60°.
25.如图,CD是经过∠BCA顶点C的一条直线,且直线CD经过∠BCA的内部,点E,F在射线CD上,已知CA=CB且∠BEC=∠CFA=∠α.
(1)如图1,若∠BCA=80°,∠α=100°,问EF=BE﹣AF,成立吗?说明理由.
(2)将(1)中的已知条件改成∠BCA=∠β,∠α+∠β=180°(如图2),问EF=BE﹣AF仍成立吗?说明理由.

【考试知识点】KD:全等三角形的断定与性质.
【专题】14:证明题;553:图形的全等;67:推理能力.
【剖析】(1)依据“AAS”可以证明△BCE≌△CAF,则BE=CF;
(2)同理证明△BCE≌△CAF,则CE=AF,BE=CF,可得EF=CE﹣CF=BE﹣AF.
【解答】解:(1)EF=BE﹣AF成立,理由如下:
∵∠BCA=80°(已知),
∴∠BCE+∠ACE=80°
∵∠BEC=∠α=100°(已知),
∴∠BEF=180°﹣100°=80°(平角概念).
∴∠B+∠BCE=80°(三角形外角和定理)
∴∠B=∠ACE(等量代换).
在△BCE和△CAF中,
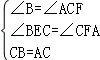 ,
,
∴△BCE≌△CAF(AAS),
∴BE=CF,AF=EC(全等三角形对应边相等).
∴EF=CF﹣CE=BE﹣AF(等量代换).
(2)EF=BE﹣AF成立,理由如下:
∵∠BCA=∠β,
∴∠BCE+∠ACE=∠β
∵∠BEC=∠α=180°﹣∠β,
∴∠BEF=180°﹣∠α=∠β.
∴∠B+∠BCE=∠β.
∴∠B=∠ACE
在△BCE和△CAF中,
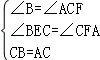 ,
,
∴△BCE≌△CAF(AAS).
∴BE=CF,AF=EC,
∴EF=CF﹣CE=BE﹣AF.
26.如图,在△ABC中,假如BD,CE分别是∠ABC,∠ACB的平分线且他们相交于点P,设∠A=n°.
(1)求∠BPC的度数(用含n的代数式表示),写出推理过程.
(2)当∠BPC=125°时,∠A=__________.
(3)当n=60°时,EB=7,BC=12,DC的长为__________.

【考试知识点】K7:三角形内角和定理.
【专题】552:三角形;553:图形的全等;67:推理能力.
【剖析】(1)依据角平分线的概念得到∠ABC=2∠PBC,∠ACB=2∠PCB.依据三角形的内角和得到结论;
(2)依据角平分线的概念得到∠ABC=2∠PBC,∠ACB=2∠PCB.依据三角形的内角和得到结论;
(3)在CB上取点G使得CG=CD,可证△BFE≌△BFG,得BE═BG,可证△CDF≌△CGF,得CD=CG,可以求得BE+CD=BC.
【解答】解:(1)∵DB、CE分别为∠ABC,∠ACB的平分线,
∴∠ABC=2∠PBC,∠ACB=2∠PCB.
∵∠A=180°﹣(∠ABC+∠ACB),
∴∠A=180°﹣2(∠PBC+∠PCB),
∴∠A=180°﹣2(180°﹣∠BPC),
∴∠A=﹣180°+2∠BPC,
∴2∠BPC=180°+∠A,
∴∠BPC=90°+![]() ∠A,
∠A,
∴∠BPC=90°+![]() n;
n;
(2)∵DB、CE分别为∠ABC,∠ACB的平分线,
∴∠ABC=2∠PBC,∠ACB=2∠PCB.
∵∠A=180°﹣(∠ABC+∠ACB),
∴∠A=180°﹣2(∠PBC+∠PCB),
∴∠A=180°﹣2(180°﹣∠BPC),
∴∠A=﹣180°+2∠BPC,
∴2∠BPC=180°+∠A,
∴∠BPC=90°+![]() ∠A,
∠A,
∴∠BPC=90°+![]() n=125°,
n=125°,
∴n=70,
∴∠A=70°;
(3)在BC上取点G使得CG=CD,
∵∠BPC=180°﹣![]() (∠ABC+∠ACB)=180°﹣
(∠ABC+∠ACB)=180°﹣![]() (180°﹣60°)=120°,
(180°﹣60°)=120°,
∴∠BPE=∠下载成本=60°,
∵在△下载成本和△CPG中,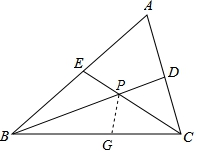 ,
,
∴△下载成本≌△CPG(SAS),
∴∠CPG=∠下载成本=60°,
∴∠BPG=120°﹣60°=60°=∠BPE,
∵在△BPE和△BPG中,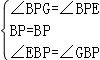 ,
,
∴△BPE≌△BPG(ASA),
∴BE=BG,
∴BE+CD=BG+CG=BC,
∵EB=7,BC=12,
∴CD=BC﹣BE=12﹣7=5.
故答案为:70°,5.








