2017-2018学年上海实验学校高中三年级(上)第三次月考数学试题
1、填空题:本大题共14个小题,每小题4分,共56分.
1.设集合M={x|x2=x},N={x|lgx≤0},则M∪N=__________.
2.已知P1(1,a1)、P2(2,a2)…Pn(n,an)、…是直线上的一列点,且a1=﹣2,a2=﹣1.2,则这个数列{an}的通项公式是__________.
3.设0<θ<![]() ,
,![]() =(sin2θ,cosplayθ),
=(sin2θ,cosplayθ),![]() =(cosplayθ,1),若
=(cosplayθ,1),若![]() ∥
∥![]() ,则tanθ=__________.
,则tanθ=__________.
4.已知单位向量![]() 与
与![]() 的夹角为α,且cosplayα=
的夹角为α,且cosplayα=![]() ,向量
,向量![]() =3
=3![]() ﹣2
﹣2![]() 与
与![]() =3
=3![]() ﹣
﹣![]() 的夹角为β,则cosplayβ=__________.
的夹角为β,则cosplayβ=__________.
5.函数y=3![]() ,(﹣1≤x≤0)的反函数是__________.
,(﹣1≤x≤0)的反函数是__________.
6.函数f(x)=cosplay![]() (sin
(sin![]() ﹣
﹣![]() cosplay
cosplay![]() )的最小正周期为__________.
)的最小正周期为__________.
7.a,b是不等的两正数,若![]()
![]() =2,则b的取值范围是__________.
=2,则b的取值范围是__________.
8.数列{an}的首项为a1=2,且an+1=![]() (a1+a2+…+an)(n∈N),记Sn为数列{an}前n项和,则Sn=__________.
(a1+a2+…+an)(n∈N),记Sn为数列{an}前n项和,则Sn=__________.
9.若向量![]() 与
与![]() 夹角为
夹角为![]() ,
,![]() ,
,![]() ,则
,则![]() =__________.
=__________.
10.已知菱形ABCD的边长为2,∠BAD=120°,点E,F分别在边BC,DC上,BC=3BE,DC=λDF,若![]() •
•![]() =1,则λ的值为__________.
=1,则λ的值为__________.
11.(理)若平面向量![]() 满足|
满足|![]() |=1(i=1,2,3,4)且
|=1(i=1,2,3,4)且![]() =0(i=1,2,3),则|
=0(i=1,2,3),则|![]() |可能的值有__________个.
|可能的值有__________个.
12.设f(x)是R上的奇函数,且当x≥0时,f(x)=x2,若对任意的x∈[a,a+2],不等式f(x+a)≥3f(x)恒成立,则实数a的取值范围是__________.
13.记Sn=[log21]+[log22]+[log23]+…+[log2n](其中[x]表示低于x的最大整数,如[0.9]=0,[2.6]=2),则S2017=__________.
14.给定0≤x0<1对所有整数n>0,令 ,则使x0=x6成立的x0的个数为__________.
,则使x0=x6成立的x0的个数为__________.
2、选择题(每题5分,满分20分)
15.在△ABC中,“cosplayA+sinA=cosplayB+sinB”是“C=90°”的()
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.非充分非必要条件
16.函数f(x)=cosplay(ωx+φ)的部分图象如图所示,则f(x)的单调递减区间为()

A.(kπ﹣![]() ,kπ+
,kπ+![]() ),k∈Z B.(2kπ﹣
),k∈Z B.(2kπ﹣![]() ,2kπ+
,2kπ+![]() ),k∈Z
),k∈Z
C.(k﹣![]() ,k﹣
,k﹣![]() ),k∈Z D.(2k﹣
),k∈Z D.(2k﹣![]() ,2k+
,2k+![]() ),k∈Z
),k∈Z
17.已知两个不相等的非零向量![]() ,
,![]() ,两组向量
,两组向量![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 和
和![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 均由2个
均由2个![]() 和3个
和3个![]() 排列而成,记S=
排列而成,记S=![]() •
•![]() +
+![]() •
•![]() +
+![]() •
•![]() +
+![]() •
•![]() +
+![]() •
•![]() ,Smin表示S所大概取值中的最小值,则下列命题中
,Smin表示S所大概取值中的最小值,则下列命题中
(1)S有5个不一样的值;(2)若![]() ⊥
⊥![]() 则Smin与|
则Smin与|![]() |无关;(3)若
|无关;(3)若![]() ∥
∥![]() 则Smin与|
则Smin与|![]() |无关;(4)若|
|无关;(4)若|![]() |>4|
|>4|![]() |,则Smin>0;(5)若|
|,则Smin>0;(5)若|![]() |=2|
|=2|![]() |,Smin=8|
|,Smin=8|![]() |2,则
|2,则![]() 与
与![]() 的夹角为
的夹角为![]() .正确的是()
.正确的是()
A.(1)(2) B.(2)(4) C.(3)(5) D.(1)(4)
18.记[x]为低于实数x的最大整数,比如:[2]=2,[1.5]=1,[﹣0.3]=﹣1,设a为正整数,数列{xn}满足:x1=a, ,现有下列命题:
,现有下列命题:
①当a=5时,数列{xn}的前3项依次为5,3,2;
②对数列{xn}都存在正整数k,当n≥k时,总有xn=xk;
③当n≥1时,![]() ;
;
④对某个正整数k,若xk+1≥xk,则![]() ;
;
其中的真命题个数为()
A.4 B.3 C.2 D.1
3、答卷(本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.)
19.已知函数![]()
(1)求函数f(x)的值域,并写出函数f(x)的单调递增区间;
(2)若![]() ,且
,且![]() ,计算cosplay2θ的值.
,计算cosplay2θ的值.
20.“活水围网”养鱼技术具备养殖密度高、经济效益好的特征.研究表明:“活水围网”养鱼时,某种鱼在肯定的条件下,每尾鱼的平均成长速度v(单位:千克/年)是养殖密度x(单位:尾/立方米)的函数.当x低于4(尾/立方米)时,v的值为2(千克/年);当4≤x≤20时,v是x的一次函数;当x达到20(尾/立方米)时,因缺氧等缘由,v的值为0(千克/年).
(1)当0<x≤20时,求函数v(x)的表达式;
(2)当养殖密度x为多大时,鱼的年成长量(单位:千克/立方米)f(x)=x•v(x)能达到最大,并求出最大值.
21.已知函数f(x)=2![]() sin(
sin(![]() +
+![]() )sin(
)sin(![]() ﹣
﹣![]() )﹣sin(π+x),且函数y=g(x)的图象与函数y=f(x)的图象关于直线x=
)﹣sin(π+x),且函数y=g(x)的图象与函数y=f(x)的图象关于直线x=![]() 对称.
对称.
(1)若存在x∈[0,![]() ),使等式[g(x)]2﹣mg(x)+2=0成立,求实数m的最大值和最小值
),使等式[g(x)]2﹣mg(x)+2=0成立,求实数m的最大值和最小值
(2)若当x∈[0,![]() ]时不等式f(x)+ag(﹣x)>0恒成立,求a的取值范围.
]时不等式f(x)+ag(﹣x)>0恒成立,求a的取值范围.
22.设Sn是各项均为非零实数的数列{an}的前n项和,给出如下两个命题上:命题p:{an}是等差数列;命题q:等式![]() 对任意n(n∈N*)恒成立,其中k,b是常数.
对任意n(n∈N*)恒成立,其中k,b是常数.
(1)若p是q的充分条件,求k,b的值;
(2)对于(1)中的k与b,问p是不是为q的必要条件,请说明理由;
(3)若p为真命题,对于给定的正整数n(n>1)和正数M,数列{an}满足条件![]() ,试求Sn的最大值.
,试求Sn的最大值.
23.已知λ,μ为常数,且为正整数,λ为质数且大于2,无穷数列{an}的各项均为正整数,其前n项和为Sn,对任意正整数n,2Sn=λan﹣μ,数列{an}中任意两不同项的和构成集合A.
(1)证明无穷数列{an}为等比数列,并求λ的值;
(2)假如2010∈A,求μ的值;
(3)当n≥1,设集合![]() 中元素的个数记为bn,求bn.
中元素的个数记为bn,求bn.
2017-2018学年上海实验学校高中三年级(上)第三次月考数学试题
参考答案与考试试题分析
1、填空题:本大题共14个小题,每小题4分,共56分.
1.设集合M={x|x2=x},N={x|lgx≤0},则M∪N=__________________________________________________.
【考试知识点】并集及其运算.
【剖析】求解一元二次方程化简M,求解对数不等式化简N,然后取并集得答案.
【解答】解:∵M={x|x2=x}={0,1},N={x|lgx≤0}=(0,1],
则M∪N=[0,1].
故答案为:[0,1].
2.已知P1(1,a1)、P2(2,a2)…Pn(n,an)、…是直线上的一列点,且a1=﹣2,a2=﹣1.2,则这个数列{an}的通项公式是______________________________.
【考试知识点】数列递推式.
【剖析】通过设直线方程并代入P1(1,﹣2)、P2(2,﹣1.2)计算,进而可得结论.
【解答】解:设所在直线方程为:y=kx+b,
∵a1=﹣2,a2=﹣1.2,
∴![]() ,解得
,解得![]() ,
,
∴直线方程为:y=0.8x﹣2.8,
∴an=0.8n﹣2.8,
故答案为:an=0.8n﹣2.8.
3.设0<θ<![]() ,
,![]() =(sin2θ,cosplayθ),
=(sin2θ,cosplayθ),![]() =(cosplayθ,1),若
=(cosplayθ,1),若![]() ∥
∥![]() ,则tanθ=__________
,则tanθ=__________![]() __________.
__________.
【考试知识点】二倍角的正弦;平面向量共线(平行)的坐标表示.
【剖析】借助向量共线定理、倍角公式、同角三角函数基本关系式即可得出.
【解答】解:∵![]() =(sin2θ,cosplayθ),
=(sin2θ,cosplayθ),![]() =(cosplayθ,1),
=(cosplayθ,1),![]() ∥
∥![]() ,
,
∴sin2θ﹣cosplay2θ=0,
∴2sinθcosplayθ=cosplay2θ,
∵0<θ<![]() ,∴cosplayθ≠0.
,∴cosplayθ≠0.
∴2tanθ=1,
∴tanθ=![]() .
.
故答案为:![]() .
.
4.已知单位向量![]() 与
与![]() 的夹角为α,且cosplayα=
的夹角为α,且cosplayα=![]() ,向量
,向量![]() =3
=3![]() ﹣2
﹣2![]() 与
与![]() =3
=3![]() ﹣
﹣![]() 的夹角为β,则cosplayβ=__________
的夹角为β,则cosplayβ=__________![]() __________.
__________.
【考试知识点】数目积表示两个向量的夹角.
【剖析】转化向量为平面直角坐标系中的向量,通过向量的数目积求出所求向量的夹角.
【解答】解:单位向量![]() 与
与![]() 的夹角为α,且cosplayα=
的夹角为α,且cosplayα=![]() ,可以
,可以![]() =(1,0),
=(1,0),![]() =
=![]() ,
,
![]() =3
=3![]() ﹣2
﹣2![]() =(
=(![]() ),
),![]() =3
=3![]() ﹣
﹣![]() =(
=(![]() ),
),
∴cosplayβ=![]() =
=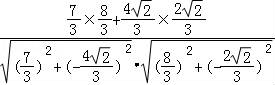 =
=![]() .
.
故答案为:![]() .
.
5.函数y=3![]() ,(﹣1≤x≤0)的反函数是__________
,(﹣1≤x≤0)的反函数是__________![]() ______________________________
______________________________![]() ______________________________.
______________________________.
【考试知识点】反函数.
【剖析】依据已知中函数y=3![]() ,用y表示x,进而可得原函数的反函数.
,用y表示x,进而可得原函数的反函数.
【解答】解:∵﹣1≤x≤0时,y=3![]() ∈[
∈[![]() ,1],
,1],
则x2﹣1=log3y,
则x2=log3y+1,
则x=![]() ,y∈[
,y∈[![]() ,1],
,1],
即函数y=3![]() ,(﹣1≤x≤0)的反函数是y=
,(﹣1≤x≤0)的反函数是y=![]() ,x∈[
,x∈[![]() ,1],
,1],
故答案为:y=![]() ,x∈[
,x∈[![]() ,1]
,1]
6.函数f(x)=cosplay![]() (sin
(sin![]() ﹣
﹣![]() cosplay
cosplay![]() )的最小正周期为__________.
)的最小正周期为__________.
【考试知识点】三角函数的周期性及其求法.
【剖析】借助三角函数的倍角公式将函数进行化简,即可得到结论.
【解答】解:f(x)=cosplay![]() (sin
(sin![]() ﹣
﹣![]() cosplay
cosplay![]() )=cosplay
)=cosplay![]() sin
sin![]() ﹣
﹣![]() cosplay2
cosplay2![]() )=
)=![]() sinx﹣
sinx﹣![]() ×
×![]() =
=![]() sinx﹣
sinx﹣![]() cosplayx﹣
cosplayx﹣![]() =sin(x
=sin(x![]() )
)![]() ,
,
则函数的周期T=![]() =2π,
=2π,
故答案为:2π
7.a,b是不等的两正数,若![]()
![]() =2,则b的取值范围是__________.
=2,则b的取值范围是__________.
【考试知识点】极限及其运算.
【剖析】当a>b时,![]()
![]() =
=![]()
 =a,进而求出b的范围.
=a,进而求出b的范围.
【解答】解:a,b是不等的两正数,且![]()
![]() =2,
=2,
须对a,b作如下讨论:
①当a>b时,![]()
![]() =0,则
=0,则![]()
![]() =
=![]()
 =a,
=a,
所以,a=2,因此,b∈(0,2),
②当a<b时,则![]()
![]() =﹣b=2,
=﹣b=2,
而b>0,故不合题意,舍去.
综合以上讨论得,b∈(0,2),
故答案为:(0,2).
8.数列{an}的首项为a1=2,且an+1=![]() (a1+a2+…+an)(n∈N),记Sn为数列{an}前n项和,则Sn=__________
(a1+a2+…+an)(n∈N),记Sn为数列{an}前n项和,则Sn=__________![]() __________.
__________.
【考试知识点】数列的求和.
【剖析】察看已知可得![]() ,
,![]() 两式相减可得{an}是从第二项开始的等比数列,代入等比数列的前n和公式求解
两式相减可得{an}是从第二项开始的等比数列,代入等比数列的前n和公式求解
【解答】解:由题意可得![]()
当n![]() 两式相减得,
两式相减得,![]()
从而有![]() ,
,![]()
数列 an从第二项开始的等比数列,公比为![]()
∴Sn=a1+a2+a3+…+an=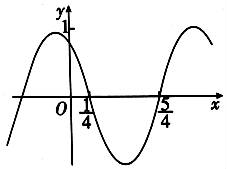
故答案为:![]()
9.若向量![]() 与
与![]() 夹角为
夹角为![]() ,
,![]() ,
,![]() ,则
,则![]() =__________.
=__________.
【考试知识点】平面向量数目积的运算.
【剖析】运用向量数目积的概念和性质,向量的平方即为模的平方,化简整理解方程即可得到所求值.
【解答】解:向量![]() 与
与![]() 夹角为
夹角为![]() ,
,![]() ,
,![]() ,
,
可得![]() 2﹣
2﹣![]() •
•![]() ﹣6
﹣6![]() 2=﹣72,
2=﹣72,
即有|![]() |2﹣4|
|2﹣4|![]() |•cosplay
|•cosplay![]() ﹣6×16=﹣72,
﹣6×16=﹣72,
即为|![]() |2﹣2|
|2﹣2|![]() |﹣24=0,
|﹣24=0,
解得|![]() |=6(﹣4舍去).
|=6(﹣4舍去).
故答案为:6.
10.已知菱形ABCD的边长为2,∠BAD=120°,点E,F分别在边BC,DC上,BC=3BE,DC=λDF,若![]() •
•![]() =1,则λ的值为__________.
=1,则λ的值为__________.
【考试知识点】平面向量数目积的运算.
【剖析】依据向量的基本定理,结合数目积的运算公式,打造方程即可得到结论.
【解答】解:∵BC=3BE,DC=λDF,
∴![]() =
=![]()
![]() ,
,![]() =
=![]()
![]() ,
,
![]() =
=![]() +
+![]() =
=![]() +
+![]()
![]() =
=![]() +
+![]()
![]() ,
,![]() =
=![]() +
+![]() =
=![]() +
+![]()
![]() =
=![]() +
+![]()
![]() ,
,
∵菱形ABCD的边长为2,∠BAD=120°,
∴|![]() |=|
|=|![]() |=2,
|=2,![]() •
•![]() =2×2×cosplay120°=﹣2,
=2×2×cosplay120°=﹣2,
∵![]() •
•![]() =1,
=1,
∴(![]() +
+![]()
![]() )•(
)•(![]() +
+![]()
![]() )=
)=![]()
![]() +
+![]()
![]() +(1+
+(1+![]() )
)![]() •
•![]() =1,
=1,
即![]() ×4+
×4+![]() ×4﹣2(1+
×4﹣2(1+![]() )=1,
)=1,
整理得![]() ,
,
解得λ=2,
故答案为:2.
11.(理)若平面向量![]() 满足|
满足|![]() |=1(i=1,2,3,4)且
|=1(i=1,2,3,4)且![]() =0(i=1,2,3),则|
=0(i=1,2,3),则|![]() |可能的值有__________个.
|可能的值有__________个.
【考试知识点】平面向量数目积的运算;向量的模.
【剖析】由![]() =0可得
=0可得![]() ,分类作图可得结论.
,分类作图可得结论.
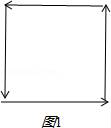
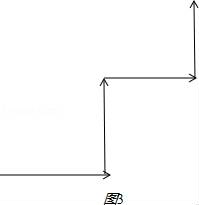
【解答】解:由![]() =0可得
=0可得![]() ,
,
若四向量首尾相连构成正方形时(图1),|![]() |=0,
|=0,
当四向量如图2所示时,|![]() |=2,
|=2,
当四向量如图3所示时,|![]() |=2
|=2![]() ,
,
故答案为:3

12.设f(x)是R上的奇函数,且当x≥0时,f(x)=x2,若对任意的x∈[a,a+2],不等式f(x+a)≥3f(x)恒成立,则实数a的取值范围是____________________![]() ______________________________.
______________________________.
【考试知识点】函数恒成立问题.
【剖析】由当x≥0时,f(x)=x2,函数是奇函数,可得当x<0时,f(x)=﹣x2,从而f(x)在R上是单调递增函数,且满足3f(x)=f(![]() x),再依据不等式f(x+a)≥3f(x)=f(
x),再依据不等式f(x+a)≥3f(x)=f(![]() x)在[a,a+2]恒成立,可得x+a≥
x)在[a,a+2]恒成立,可得x+a≥![]() x在[a,a+2]恒成立,即可得出答案.
x在[a,a+2]恒成立,即可得出答案.
【解答】解:∵当x≥0时,f(x)=x2,
∴此时函数f(x)单调递增,
∵f(x)是概念在R上的奇函数,
∴函数f(x)在R上单调递增.
若对任意x∈[a,a+2],不等式f(x+a)≥3f(x)恒成立,
∵3f(x)=3x2=(![]() x)2=f(
x)2=f(![]() x),
x),
∴f(x+a)≥f(![]() x)恒成立,
x)恒成立,
则x+a≥![]() x恒成立,
x恒成立,
即a≥﹣x+![]() x=(
x=(![]() ﹣1)x恒成立.
﹣1)x恒成立.
∵x∈[a,a+2],
∴[(![]() ﹣1)x]max=(
﹣1)x]max=(![]() ﹣1)(a+2),
﹣1)(a+2),
即a≥(![]() ﹣1)(a+2),
﹣1)(a+2),
解得a≥![]() .
.
即实数a的取值范围是[![]() ,+∞).
,+∞).
故答案为:[![]() ,+∞).
,+∞).
13.记Sn=[log21]+[log22]+[log23]+…+[log2n](其中[x]表示低于x的最大整数,如[0.9]=0,[2.6]=2),则S2017=__________.
【考试知识点】对数的运算性质.
【剖析】借助[x]的性质和对数性质及运算法则得S2017=[log21]+[log22]+[log23]+…+[log22017]=0×1+1×2+2×4+3×8+4×16+5×32+6×64+7×128+8×256+9×512+10×994,由此能求出结果.
【解答】解:∵Sn=[log21]+[log22]+[log23]+…+[log2n](其中[x]表示低于x的最大整数,
∴S2017=[log21]+[log22]+[log23]+…+[log22017]
=0×1+1×2+2×4+3×8+4×16+5×32+6×64+7×128+8×256+9×512+10×994=18134.
故答案为:
18134.
14.给定0≤x0<1对所有整数n>0,令 ,则使x0=x6成立的x0的个数为__________.
,则使x0=x6成立的x0的个数为__________.
【考试知识点】数列递推式.
【剖析】由题意依据分段函数的取值范围,则x1=2x0∈[0,![]() ),x2=2x1∈[0,
),x2=2x1∈[0,![]() ),x3=2x2∈[0,
),x3=2x2∈[0,![]() ),x4=2x3∈[0,
),x4=2x3∈[0,![]() ),x5=2x4∈[0,
),x5=2x4∈[0,![]() ),x6=2x5,则x6=2x5=22x4=…=26x0=x0,得x0=0,此时 x0 的值有一个;同理,当 x0∈[
),x6=2x5,则x6=2x5=22x4=…=26x0=x0,得x0=0,此时 x0 的值有一个;同理,当 x0∈[![]() ,
,![]() )时,x0 的值有22个,当x0∈[
)时,x0 的值有22个,当x0∈[![]() ,
,![]() )时,x0 的值有23个,当x0∈[
)时,x0 的值有23个,当x0∈[![]() ,
,![]() )时,x0 的值有24个,当x0∈[
)时,x0 的值有24个,当x0∈[![]() ,1)时,x0 的值有25个,综上,则使 x0=x6 成立的x0的个数为1+1+2+22+23+24+25=64个,
,1)时,x0 的值有25个,综上,则使 x0=x6 成立的x0的个数为1+1+2+22+23+24+25=64个,
【解答】解:.依题意, ,当x0∈[0,
,当x0∈[0,![]() ) 时,
) 时,
x1=2x0∈[0,![]() ),x2=2x1∈[0,
),x2=2x1∈[0,![]() ),x3=2x2∈[0,
),x3=2x2∈[0,![]() ),x4=2x3∈[0,
),x4=2x3∈[0,![]() ),x5=2x4∈[0,
),x5=2x4∈[0,![]() ),x6=2x5,
),x6=2x5,
则x6=2x5=22x4=…=26x0=x0,得x0=0,此时 x0 的值有一个;
当x0∈[![]() ,
,![]() ) 时,
) 时,
x1=2x0∈[![]() ,
,![]() ),x2=2x1∈[
),x2=2x1∈[![]() ,
,![]() ),x3=2x2∈[
),x3=2x2∈[![]() ,
,![]() ),x4=2x3∈[
),x4=2x3∈[![]() ,
,![]() ),x5=2x4∈[
),x5=2x4∈[![]() ,1),x6=2x5﹣1,
,1),x6=2x5﹣1,
故有x6=2x5﹣1=22x4﹣1=…=26x0﹣1=x0,得x0=![]() ,此时x0 的值有一个;
,此时x0 的值有一个;
当x0∈[![]() ,
,![]() ) 时,x1=2x0∈[
) 时,x1=2x0∈[![]() ,
,![]() ),x2=2x1∈[
),x2=2x1∈[![]() ,
,![]() ),x3=2x2∈[
),x3=2x2∈[![]() ,
,![]() ),x4=2x3∈[
),x4=2x3∈[![]() ,1),x5=2x4∈[0,1),x6=2x5﹣1,
,1),x5=2x4∈[0,1),x6=2x5﹣1,
当x5∈[0,![]() ),x6=2x5=2(2x4﹣1)=…=26x0﹣2=x0,得:x0=
),x6=2x5=2(2x4﹣1)=…=26x0﹣2=x0,得:x0=![]() ,
,
当x5∈[![]() ,1),x6=2x5=2(2x4﹣1)﹣1=…=26x0﹣3=x0,得:x0=
,1),x6=2x5=2(2x4﹣1)﹣1=…=26x0﹣3=x0,得:x0=![]() =
=![]() ,
,
此时x0 的值有2个;
同理,当 x0∈[![]() ,
,![]() )时,x0 的值有22个,
)时,x0 的值有22个,
当x0∈[![]() ,
,![]() )时,x0 的值有23个,
)时,x0 的值有23个,
当x0∈[![]() ,
,![]() )时,x0 的值有24个,
)时,x0 的值有24个,
当x0∈[![]() ,1)时,x0 的值有25个,
,1)时,x0 的值有25个,
综上,则使 x0=x6 成立的x0的个数为1+1+2+22+23+24+25=64个,
故答案为:64.
2、选择题(每题5分,满分20分)
15.在△ABC中,“cosplayA+sinA=cosplayB+sinB”是“C=90°”的()
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.非充分非必要条件
【考试知识点】充要条件.
【剖析】对两个条件,“cosplayA+sinA=cosplayB+sinB”与“C=90°”的关系,结合三角函数的概念,对选项进行判断
【解答】解:“C=90°”成立时,有A+B=90°,故肯定有“cosplayA+sinA=cosplayB+sinB”成立
又当A=B时cosplayA+sinA=cosplayB+sinB”成立,即“cosplayA+sinA=cosplayB+sinB”得不出“C=90°”成立
所以“cosplayA+sinA=cosplayB+sinB”是“C=90°”的必要非充分条件
故选B.
16.函数f(x)=cosplay(ωx+φ)的部分图象如图所示,则f(x)的单调递减区间为()

A.(kπ﹣![]() ,kπ+
,kπ+![]() ),k∈Z B.(2kπ﹣
),k∈Z B.(2kπ﹣![]() ,2kπ+
,2kπ+![]() ),k∈Z
),k∈Z
C.(k﹣![]() ,k﹣
,k﹣![]() ),k∈Z D.(2k﹣
),k∈Z D.(2k﹣![]() ,2k+
,2k+![]() ),k∈Z
),k∈Z
【考试知识点】余弦函数的图象.
【剖析】依据图象求出函数的分析式,结合三角函数的性质即可得到结论.
【解答】解:从图象可以看出:图象过相邻的两个零点为(![]() ,0),(
,0),(![]() ,0),
,0),
可得:T=2×![]() =2,
=2,
∴ω=![]() =π,
=π,
∴f(x)=cosplay(πx+φ),将点(![]() ,0)带入可得:cosplay(
,0)带入可得:cosplay(![]() +φ)=0,
+φ)=0,
令![]() +φ=
+φ=![]() ,可得φ=
,可得φ=![]() ,
,
∴f(x)=cosplay(πx+![]() ),
),
由![]() ,单点递减(k∈Z),
,单点递减(k∈Z),
解得:2k﹣![]() ≤x≤2k+
≤x≤2k+![]() ,k∈Z.
,k∈Z.
故选D
17.已知两个不相等的非零向量![]() ,
,![]() ,两组向量
,两组向量![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 和
和![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 均由2个
均由2个![]() 和3个
和3个![]() 排列而成,记S=
排列而成,记S=![]() •
•![]() +
+![]() •
•![]() +
+![]() •
•![]() +
+![]() •
•![]() +
+![]() •
•![]() ,Smin表示S所大概取值中的最小值,则下列命题中
,Smin表示S所大概取值中的最小值,则下列命题中
(1)S有5个不一样的值;(2)若![]() ⊥
⊥![]() 则Smin与|
则Smin与|![]() |无关;(3)若
|无关;(3)若![]() ∥
∥![]() 则Smin与|
则Smin与|![]() |无关;(4)若|
|无关;(4)若|![]() |>4|
|>4|![]() |,则Smin>0;(5)若|
|,则Smin>0;(5)若|![]() |=2|
|=2|![]() |,Smin=8|
|,Smin=8|![]() |2,则
|2,则![]() 与
与![]() 的夹角为
的夹角为![]() .正确的是()
.正确的是()
A.(1)(2) B.(2)(4) C.(3)(5) D.(1)(4)
【考试知识点】平面向量数目积的运算.
【剖析】依题意,可求得S有3种结果:①S=2![]() +3
+3![]() ;②S=
;②S=![]() ;③S=4
;③S=4![]() .可判断(1)错误;进一步剖析有S1﹣S2=S2﹣S3=
.可判断(1)错误;进一步剖析有S1﹣S2=S2﹣S3=![]() ,即S中最小为S3;再对(2)(3)(4)(5)逐一剖析即可得答案.
,即S中最小为S3;再对(2)(3)(4)(5)逐一剖析即可得答案.
【解答】解:∵xi,yi(i=1,2,3,4,5)均由2个![]() 和3个
和3个![]() 排列而成,
排列而成,
∴S=xiyi可能状况有三种:①S=2![]() +3
+3![]() ;②S=
;②S=![]() ;③S=4
;③S=4![]() .故(1)错误;
.故(1)错误;
∵S1﹣S2=S2﹣S3=![]() ,∴S中最小为S3.
,∴S中最小为S3.
若![]() ,则Smin=S3=
,则Smin=S3=![]() ,与|
,与|![]() |无关,故(2)正确;
|无关,故(2)正确;
若![]() ,则Smin=S3=4
,则Smin=S3=4![]() ,与|
,与|![]() |有关,故(3)错误;
|有关,故(3)错误;
若|![]() |>4|
|>4|![]() |,则Smin=S3=4|
|,则Smin=S3=4|![]() |•|
|•|![]() |cosplayθ+
|cosplayθ+![]() >﹣4|
>﹣4|![]() |•|
|•|![]() |+
|+![]() >﹣
>﹣![]() +
+![]() =0,故(4)正确;
=0,故(4)正确;
若|![]() |=2|
|=2|![]() |,Smin=S3=8
|,Smin=S3=8![]() cosplayθ+4
cosplayθ+4![]() =8
=8![]() ,
,
∴2cosplayθ=1,∴θ=![]() ,
,
即![]() 与
与![]() 的夹角为
的夹角为![]() ,(5)错误.
,(5)错误.
综上所述,命题正确的是(2)(4),
故选:B.
18.记[x]为低于实数x的最大整数,比如:[2]=2,[1.5]=1,[﹣0.3]=﹣1,设a为正整数,数列{xn}满足:x1=a, ,现有下列命题:
,现有下列命题:
①当a=5时,数列{xn}的前3项依次为5,3,2;
②对数列{xn}都存在正整数k,当n≥k时,总有xn=xk;
③当n≥1时,![]() ;
;
④对某个正整数k,若xk+1≥xk,则![]() ;
;
其中的真命题个数为()
A.4 B.3 C.2 D.1
【考试知识点】命题的真伪判断与应用.
【剖析】根据给出的概念对四个命题结合数列的常识逐一进行判断真伪.对于①:列举即可;对于②:需举反例;对于③,可用数学总结法加以证明;对于④:可由总结推理判断其正误.
【解答】解:对于①:当a=5时,x1=5,x2= =3,x3=
=3,x3= =2,故①正确;
=2,故①正确;
对于②:当a=1时,x2= =1,x3=1,xk恒等于[
=1,x3=1,xk恒等于[![]() ]=1;
]=1;
当a=2时,x1=2,x2=![]() =1,x3=
=1,x3= =1,
=1,
∴当k≥2时,恒有xk=[![]() ]=1;
]=1;
当a=3时,x1=3,x2=2,x3=1,x4=2,x5=1,x6=2,x7=1,…,
此时数列{xn}除第一项外,从第二项起未来的项以2为周期重复出现,
因此没有正整数k,使得n≥k时,总有xn=xk,故②不正确;
对于③:在xn+[![]() ]中,当
]中,当![]() 为正整数时,xn+[
为正整数时,xn+[![]() ]=xn+
]=xn+![]() ≥2
≥2![]() ,
,
∴xn+1=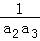 ≥[
≥[![]() ]=[
]=[![]() ];
];
当![]() 不是正整数时,令[
不是正整数时,令[![]() ]=
]=![]() ﹣t,t为
﹣t,t为![]() 的小数部分,
的小数部分,
0<t<1,xn+1= =
= >[
>[![]() ]=[
]=[![]() ﹣
﹣![]() ]=[
]=[![]() ],
],
∴xn+1≥[![]() ],∴xn≥[
],∴xn≥[![]() ],∴xn>
],∴xn>![]() ﹣1,故③正确;
﹣1,故③正确;
由以上论证知,存在某个正整数k,若xk+1≥xk,
则当n≥k时,总有xn=[![]() ],故④正确.
],故④正确.
故选:B
3、答卷(本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.)
19.已知函数![]()
(1)求函数f(x)的值域,并写出函数f(x)的单调递增区间;
(2)若![]() ,且
,且![]() ,计算cosplay2θ的值.
,计算cosplay2θ的值.
【考试知识点】三角函数中的恒等变换应用;二倍角的余弦.
【剖析】(1)借助二倍角公式、辅助角公式化简函数,依据角的范围,即可求函数f(x)的值域,借助正弦函数的单调性,即可求得函数f(x)的单调递增区间;
(2)由![]() ,
,![]() ,可得
,可得![]() =
=![]() ,再借助角的变换计算cosplay2θ的值.
,再借助角的变换计算cosplay2θ的值.
【解答】解:(1)![]() …
…
因为![]() ,
,
∴函数f(x)的值域为[﹣2,2]…
由![]() 得
得![]()
∴函数f(x)的单调的增区间为![]() ,k∈Z…
,k∈Z…
(2)∵![]() ,…
,…
∴![]() ,
,
∴![]() …
…
∵![]() ,
,
∴![]() =
=![]()
∴![]() …
…
∴![]() …
…
=![]() …
…
20.“活水围网”养鱼技术具备养殖密度高、经济效益好的特征.研究表明:“活水围网”养鱼时,某种鱼在肯定的条件下,每尾鱼的平均成长速度v(单位:千克/年)是养殖密度x(单位:尾/立方米)的函数.当x低于4(尾/立方米)时,v的值为2(千克/年);当4≤x≤20时,v是x的一次函数;当x达到20(尾/立方米)时,因缺氧等缘由,v的值为0(千克/年).
(1)当0<x≤20时,求函数v(x)的表达式;
(2)当养殖密度x为多大时,鱼的年成长量(单位:千克/立方米)f(x)=x•v(x)能达到最大,并求出最大值.
【考试知识点】函数模型的选择与应用.
【剖析】(1)由题意:当0<x≤4时,v(x)=2.当4<x≤20时,设v(x)=ax+b,v(x)=ax+b在[4,20]是减函数,由已知得![]() ,能求出函数v(x).
,能求出函数v(x).
(2)依题意并由(1),得f(x)=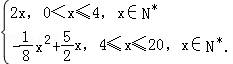 ,当0≤x≤4时,f(x)为增函数,由此能求出fmax(x)=f(4),由此能求出结果.
,当0≤x≤4时,f(x)为增函数,由此能求出fmax(x)=f(4),由此能求出结果.
【解答】解:(1)由题意:当0<x≤4时,v(x)=2.…
当4<x≤20时,设v(x)=ax+b,显然v(x)=ax+b在[4,20]是减函数,
由已知得![]() ,
,
解得![]() …
…
故函数v(x)= …
…
(2)依题意并由(1),
得f(x)=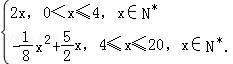 ,…
,…
当0≤x≤4时,f(x)为增函数,
故fmax(x)=f(4)=4×2=8.…
当4≤x≤20时,f(x)=﹣![]() =﹣
=﹣![]() =﹣
=﹣![]() +
+![]() ,
,
fmax(x)=f(10)=12.5.…
所以,当0<x≤20时,f(x)的最大值为12.5.
当养殖密度为10尾/立方米时,
鱼的年成长量能达到最大,最大值约为12.5千克/立方米.…
21.已知函数f(x)=2![]() sin(
sin(![]() +
+![]() )sin(
)sin(![]() ﹣
﹣![]() )﹣sin(π+x),且函数y=g(x)的图象与函数y=f(x)的图象关于直线x=
)﹣sin(π+x),且函数y=g(x)的图象与函数y=f(x)的图象关于直线x=![]() 对称.
对称.
(1)若存在x∈[0,![]() ),使等式[g(x)]2﹣mg(x)+2=0成立,求实数m的最大值和最小值
),使等式[g(x)]2﹣mg(x)+2=0成立,求实数m的最大值和最小值
(2)若当x∈[0,![]() ]时不等式f(x)+ag(﹣x)>0恒成立,求a的取值范围.
]时不等式f(x)+ag(﹣x)>0恒成立,求a的取值范围.
【考试知识点】三角函数中的恒等变换应用;正弦函数的图象.
【剖析】(1)先求出f(x),g(x)的分析式,确定g(x)∈[1,2],等式[g(x)]2﹣mg(x)+2=0,可化为m=y+![]() ,即可求实数m的最大值和最小值
,即可求实数m的最大值和最小值
(2)当x∈[0,![]() ]时,f(x)∈[﹣
]时,f(x)∈[﹣![]() ,1],g(﹣x)∈[﹣1,1],借助当x∈[0,
,1],g(﹣x)∈[﹣1,1],借助当x∈[0,![]() ]时不等式f(x)+ag(﹣x)>0恒成立,求a的取值范围.
]时不等式f(x)+ag(﹣x)>0恒成立,求a的取值范围.
【解答】解:(1)f(x)=![]() sin(x+
sin(x+![]() )+sinx=
)+sinx=![]() cosplayx+sinx=2sin(x+
cosplayx+sinx=2sin(x+![]() ).
).
函数y=g(x)的图象上取点(x,y),关于直线x=![]() 对称点的坐标为(
对称点的坐标为(![]() ﹣x,y),
﹣x,y),
代入f(x)=2sin(x+![]() ),可得y=2sin(
),可得y=2sin(![]() ﹣x),
﹣x),
x∈[0,![]() ),则
),则![]() ﹣x∈[
﹣x∈[![]() ,
,![]() ],∴y∈[1,2],
],∴y∈[1,2],
等式[g(x)]2﹣mg(x)+2=0,可化为m=y+![]() ,
,
∴y=![]() 时,m的最小值为2
时,m的最小值为2![]() ;m=1或2时,m的最大值为3;
;m=1或2时,m的最大值为3;
(2)当x∈[0,![]() ]时,f(x)∈[﹣
]时,f(x)∈[﹣![]() ,1],g(﹣x)∈[﹣1,1],
,1],g(﹣x)∈[﹣1,1],
∵当x∈[0,![]() ]时不等式f(x)+ag(﹣x)>0恒成立,
]时不等式f(x)+ag(﹣x)>0恒成立,
∴a![]() 或a
或a![]() .
.
22.设Sn是各项均为非零实数的数列{an}的前n项和,给出如下两个命题上:命题p:{an}是等差数列;命题q:等式![]() 对任意n(n∈N*)恒成立,其中k,b是常数.
对任意n(n∈N*)恒成立,其中k,b是常数.
(1)若p是q的充分条件,求k,b的值;
(2)对于(1)中的k与b,问p是不是为q的必要条件,请说明理由;
(3)若p为真命题,对于给定的正整数n(n>1)和正数M,数列{an}满足条件![]() ,试求Sn的最大值.
,试求Sn的最大值.
【考试知识点】等差数列与等比数列的综合;数列的求和.
【剖析】(1)设{an}的公差为d,借助裂项法原等式可化为![]() (
(![]() ﹣
﹣![]() +
+![]() ﹣
﹣![]() +…+
+…+![]() ﹣
﹣![]() )=
)=![]() ,整理可得(k﹣1)n+b=0对于n∈N*恒成立,从而可求得k,b的值;
,整理可得(k﹣1)n+b=0对于n∈N*恒成立,从而可求得k,b的值;
(2)当k=1,b=0时,假设p是q的必要条件,分当n=1时,当n≥2时,当n≥3时讨论即可判断结论是不是正确;
(3)由![]() +
+![]() ≤M,可设a1=rcosplayθ,an+1=rsinθ,代入求和公式Sn=
≤M,可设a1=rcosplayθ,an+1=rsinθ,代入求和公式Sn=![]() ,借助三角函数的有界性即可求得其最大值.
,借助三角函数的有界性即可求得其最大值.
【解答】解:(1)设{an}的公差为d,则原等式可化为![]() (
(![]() ﹣
﹣![]() +
+![]() ﹣
﹣![]() +…+
+…+![]() ﹣
﹣![]() )=
)=![]() ,
,
所以![]() •
•![]() =
=![]() ,
,
即(k﹣1)n+b=0对于n∈N*恒成立,所以k=1,b=0.…
(2)当k=1,b=0时,假设p是q的必要条件,即“若![]() +
+![]() +…+
+…+![]() =
=![]() ①对于任意的n(n∈N*)恒成立,则{an}为等差数列”.
①对于任意的n(n∈N*)恒成立,则{an}为等差数列”.
当n=1时,![]() =
=![]() 显然成立.…
显然成立.…
当n≥2时,若![]() +
+![]() +…+
+…+![]() =
=![]() ②,
②,
由①﹣②得,![]() =
=![]() (
(![]() ﹣
﹣![]() ),即nan﹣(n﹣1)an+1=a1③.
),即nan﹣(n﹣1)an+1=a1③.
当n=2时,a1+a3=2a2,即a1、a2、a3成等差数列,
当n≥3时,(n﹣1)an﹣1﹣(n﹣2)an=a1④,即2an=an﹣1+an+1.所以{an}为等差数列,即p是q的必要条件.…
(3)由![]() +
+![]() ≤M,可设a1=rcosplayθ,an+1=rsinθ,所以r≤
≤M,可设a1=rcosplayθ,an+1=rsinθ,所以r≤![]() .
.
设{an}的公差为d,则an+1﹣a1=nd=rsinθ﹣rcosplayθ,
所以d=![]() ,
,
所以an=rsinθ﹣![]() ,
,
Sn=![]() =
=![]() r≤
r≤![]() •
•![]() =
=![]()
![]() ,
,
所以Sn的最大值为![]() …
…
23.已知λ,μ为常数,且为正整数,λ为质数且大于2,无穷数列{an}的各项均为正整数,其前n项和为Sn,对任意正整数n,2Sn=λan﹣μ,数列{an}中任意两不同项的和构成集合A.
(1)证明无穷数列{an}为等比数列,并求λ的值;
(2)假如2010∈A,求μ的值;
(3)当n≥1,设集合![]() 中元素的个数记为bn,求bn.
中元素的个数记为bn,求bn.
【考试知识点】集合的表示法.
【剖析】(1)Sn=λan﹣μ.当n≥2时,Sn﹣1=λan﹣1﹣μ,可得![]() 为正整数,即可得出正整数λ.
为正整数,即可得出正整数λ.
(2)由(1)可得:Sn=2an﹣μ,可得an=μ•2n﹣1,因此A={μ(2i﹣1+2j﹣1)|1≤i<j,i,j∈N*},因为2015∈A,可得2015=μ(2i﹣1+2j﹣1)=μ•2i﹣1(1+2j﹣i)=5×13×31,借助2i﹣1为偶数时,上式不成立,因此必有2i﹣1=1,可得i=1,即可得出j,μ.
(3)当n≥1时,集合集合![]() ,即即5μ•3n﹣1<μ(3i﹣1+3j﹣1)<5μ•3n,1≤i<j,i,j∈N*Bn中元素的个数,等价于满足5•3n<3i+3j<5•3n+1的不同解(i,j),只有j=n+2才成立,借助5•3n<31+3n+2<32+3n+2<…<3n+3n+2<3n+1+3n+2=4•3n+1<5•3n+1,即可得出.(n∈N*).
,即即5μ•3n﹣1<μ(3i﹣1+3j﹣1)<5μ•3n,1≤i<j,i,j∈N*Bn中元素的个数,等价于满足5•3n<3i+3j<5•3n+1的不同解(i,j),只有j=n+2才成立,借助5•3n<31+3n+2<32+3n+2<…<3n+3n+2<3n+1+3n+2=4•3n+1<5•3n+1,即可得出.(n∈N*).
【解答】解:(1)当n≥2时,2Sn=λan﹣μ,2Sn﹣1=λan﹣1﹣μ,两式相减得:2an=λan﹣λan﹣1(λ为质数且大于2),![]() ,所以{an}为等比数列,又{an}各项均为正整数,则
,所以{an}为等比数列,又{an}各项均为正整数,则![]() 为正整数,λ为质数,则λ=3
为正整数,λ为质数,则λ=3
(2)由(1)得:2Sn=3an﹣μ,当n=1时,a1=μ,则![]()
所以A={μ(3i﹣1+3j﹣1)|1≤i<j,i,j∈N*}
假如2010∈A,则2010=μ(3i﹣1+3j﹣1)=μ3i﹣1(1+3j﹣i)=2×3×5×67
由于j﹣i>0,则1+3j﹣i必为不小于4的偶数,则
因1+3j﹣i=2×3时,无解;因1+3j﹣i=2×67时,无解;因1+3j﹣i=2×3×5,无解;
因1+3j﹣i=2×3×67,无解;因1+3j﹣i=2×5×67,无解;
因1+3j﹣i=2×3×5×67=2010,无解;
当1+3j﹣i=2×5⇒j﹣i=2,μ•3i﹣1=201=3×67,
当i﹣1=1时,μ=67,所以2010=67(32﹣1+34﹣1)∈A
当i﹣1=0时,μ=201,所以2010=201(31﹣1+33﹣1)∈A
综上,μ=67或μ=201
(3)当n≥1时,![]()
即5μ•3n﹣1<μ(3i﹣1+3j﹣1)<5μ•3n,1≤i<j,i,j∈N*Bn中元素的个数,等价于满足5•3n<3i+3j<5•3n+1的不同解(i,j)
假如j>n+2,则3j+3i≥3i+3n+3=3i+9•3n+1>5•3n+1,矛盾.
假如j<n+2,则3j+3i≤3i+3n+1≤3n+3n+1≤4•3n<5•3n,矛盾.
从而,j=n+2
又由于(31+3n+2)﹣5•3n=3+4•3n>0
所以5•3n<31+3n+2<32+3n+2<…<3n+3n+2<3n+1+3n+2=4•3n+1<5•3n+1
即i=1,2,…,n,n+1,共n+1个不一样的解(i,j),即共n+1个不同x∈Bn,所以![]() .
.







