1、单选题
1.下面的数,因数个数最多的是( )。
A.18 | B.22 | C.40 | D.45 |
2.![]() 和b是两个不一样的质数,那样
和b是两个不一样的质数,那样![]() 和b的积有( )个因数。
和b的积有( )个因数。
A.2 | B.3 | C.4 | D.6 |
3.下面办法中,不可以让图1变为图2的是( )。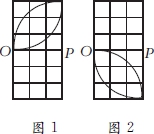
A.图1绕点O逆时针方向旋转90° |
B.图1绕点O顺时针方向旋转90° |
C.图1绕点O逆时针方向旋转270° |
D.以线段OP所在的直线为对称轴画图1的对称图形 |
4.三个小队采集树种,一小队比二小队多采集![]() 千克,三小队比二小队少采集
千克,三小队比二小队少采集![]() 千克,一小队和三小队采集的树种相差( )千克。
千克,一小队和三小队采集的树种相差( )千克。
A. | B. | C. |
|
5.龙龙用6个同样大的正方体摆成一个物体。他从正面和上面看到的图形都是![]() ,那样假如从侧面看摆成的物体,看到的图形是( )。
,那样假如从侧面看摆成的物体,看到的图形是( )。
A. | B. | C. | D. |
2、填空题
6.一个长方体的金鱼缸,长是8分米,宽是5分米,高是6分米,不小心前面的玻璃被打坏了,维修时配上的玻璃的面积是__________平方分米。
7.用小正方体搭成一个几何体,从上面和从正面看到的这个几何体的形状如图,要符合这两个条件,最少需要摆__________块,最多能摆__________块,共有__________种摆法。
8.5![]() 2,假如它是6的倍数,
2,假如它是6的倍数,![]() 里可填__________,假如它是9的倍数,
里可填__________,假如它是9的倍数,![]() 里可填__________。
里可填__________。
9.1至2008这2008个自然数中,恰好是3、5、7中两个数的倍数的数共有__________个。
10.用两个长3 cm,宽3 cm,高1 cm的长方体拼成一个大长方体,这个大长方体的表面积最大是__________,最小是__________。
3、判断题
11.除2以外所有些质数都是奇数。( )
12.长方体是特殊的正方体。( )
13.一个木箱的体积就是它的容积。( )
14.把两个一样的正方体拼成一个长方体后,体积和表面积都不变。( )
15.将一张正方形纸连续对折三次,展开后其中一份是这张纸的![]() 。( )
。( )
4、计算题
16.计算下面各图的表面积和体积。
17.找规律计算。
![]()
![]()
![]()
依据上面等式计算:![]() =。
=。
5、操作题
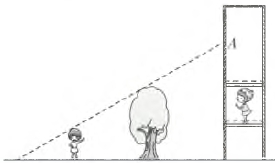
18.如图,观光电梯中的人至少上升到哪个位置时就能看到大树后面训练的人?请画出图来表示。
6、解答卷
19.用一根32 cm长的铁丝围成一个长方形,长和宽都是质数,这个长方形的面积最大是多少平方厘米?
20.一个长方体正好可以切成5个同样大小的正方体,切成的5个正方体的表面积比原来长方表面积多了200平方厘米,求原来长方体的表面积?
7、解决问题
21.把8个棱长是1厘米的小正方体拼摆在一块。假如从正面和后面看,所看到的图形面积之和是多少平方厘米?
22.体育课上,老师在筐里放了30个乒乓球,让小东去拿。不许一次拿完,也不许一个一个地拿,要每次拿的个数相同,拿到最后正好一个也不剩。小东共有多少种拿法?每种拿法各拿多少次?
答案
1、单选题
1. | 【答案】C 选项B:22的因数有1,2,11,22,共4个; 选项C:40的因数有1,2,4,5,8,10,20,40,共8个; 选项D:45的因数有1、3、5、9、15、45,共6个。 所以因数个数最多的是40。 故答案为:C。 |
2. | 【答案】C |
3. | 【答案】A |
4. | 【答案】B 所以一小队和三小队采集的树种相差 故选C。 |
5. | 【答案】A |
2、填空题
6. | 【答案】48 所以维修时配上的玻璃的面积是48平方分米。 故答案为:48。 |
7. | 【答案】8 10 9 最少需要:6+2=8;最多需要:6×2-2=10; 用10个摆:底层需要6个,上层4个有1种。 4+4+1=9,共有9种摆法。 |
8. | 【答案】2,5,8 2 假如它是9的倍数, 故答案为:2,5,8;2。 |
9. | 【答案】228 3和7的倍数有 5和7的倍数有 3、5和7的倍数有 所以恰好是3、5、7中两个数的倍数共有133-19+95-19+57-19=228。 故答案为:228。 |
10.【答案】54 cm2 42 cm2 | |
3、判断题
11. | 【答案】√ |
12. | 【答案】× |
13. | 【答案】× 所以木箱的体积大于它的容积。题干说法不正确。 故错误。 |
14. | 【答案】× 但表面积变了,降低了正方体2个面的面积,题干说法不正确。 故错误。 |
15. | 【答案】√ |
4、计算题
16. | 【答案】长方体的表面积:×2 |
17.【答案】 = = = | |
5、操作题
18.【答案】 |
6、解答卷
19. | 【答案】32÷2=16 16=3+13=5+11 13×3=39 11×5=55 39<55 答:这个长方形的面积最大是55 cm2。 |
20. | 【答案】200÷8=25 ×25 =×25 =22×25 =550 答:原来长方体的表面积是550平方厘米。 |
7、解决问题
21. | 【答案】×1×1 =12×1 =12 答:所看到的图形面积之和是12平方厘米。 |
22. | 【答案】6种。 |