__________
专题03一元二次方程及应用

![]()
【考试知识点1】一元二次方程的根的求值问题
【例1】(2019•兰州)x=1是关于x的一元二次方程x2+ax+2b=0的解,则2a+4b=()
A.﹣2 B.﹣3 C.﹣1 D.﹣6
【答案】A
【分析】把x=1代入方程x2+ax+2b=0得1+a+2b=0,
所以a+2b=﹣1,
所以2a+4b=2(a+2b)=2×(﹣1)=﹣2.
故选:A.
点睛:本题考查了一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.
【变式1-1】(2019•遂宁)已知关于x的一元二次方程(a﹣1)x2﹣2x+a2﹣1=0有一个根为x=0,则a的值为()
A.0 B.±1 C.1 D.﹣1
【答案】D
【分析】∵关于x的一元二次方程(a﹣1)x2﹣2x+a2﹣1=0有一个根为x=0,
∴a2﹣1=0,且a﹣1≠0,
则a的值为:a=﹣1.
故选:D.
点睛:此题主要考查了一元二次方程的解,注意二次项系数不可以为零.
【变式1-2】(2019•甘肃)若一元二次方程x2﹣2kx+k2=0的一根为x=﹣1,则k的值为()
A.﹣1 B.0 C.1或﹣1 D.2或0
【答案】A
【分析】把x=﹣1代入方程得:1+2k+k2=0,
解得:k=﹣1,
故选:A.
点睛:此题考查了一元二次方程的解,方程的解即为能使方程左右两边相等的未知数的值.
【考试知识点2】配办法解一元二次方程
【例2】(2019•南通)用配办法解方程x2+8x+9=0,变形后的结果正确的是()
A.(x+4)2=﹣9 B.(x+4)2=﹣7 C.(x+4)2=25 D.(x+4)2=7
【答案】D
【分析】方程x2+8x+9=0,整理得:x2+8x=﹣9,
配方得:x2+8x+16=7,即(x+4)2=7,
故选:D.
点睛:此题考查知道一元二次方程﹣配办法,熟练学会完全平方公式是解本题的重点.
【变式2-1】(2019•金华)用配办法解方程x2﹣6x﹣8=0时,配方结果正确的是()
A.(x﹣3)2=17 B.(x﹣3)2=14 C.(x﹣6)2=44 D.(x﹣3)2=1
【答案】A
【分析】用配办法解方程x2﹣6x﹣8=0时,配方结果为(x﹣3)2=17,
故选:A.
点睛:此题考查知道一元二次方程﹣配办法,熟练学会完全平方公式是解本题的重点.
【考试知识点3】因式分解法解一元二次方程
【例3】(2019•桂林)一元二次方程(x﹣3)(x﹣2)=0的根是______________________________.
【答案】x1=3,x2=2
【分析】x﹣3=0或x﹣2=0,
所以x1=3,x2=2.
故答案为x1=3,x2=2.
点睛:本题考查知道一元二次方程﹣因式分解法:因式分解法就是借助因式分解求出方程的解的办法,这种办法方便易用,是解一元二次方程最常见的办法.
【变式3-1】(2019•十堰)对于实数a,b,概念运算“◎”如下:a◎b=(a+b)2﹣(a﹣b)2.若(m+2)◎(m﹣3)=24,则m=__________.
【答案】﹣3或4
【分析】依据题意得[(m+2)+(m﹣3)]2﹣[(m+2)﹣(m﹣3)]2=24,
(2m﹣1)2﹣49=0,
(2m﹣1+7)(2m﹣1﹣7)=0,
2m﹣1+7=0或2m﹣1﹣7=0,
所以m1=﹣3,m2=4.
故答案为﹣3或4.
点睛:本题考查知道一元二次方程﹣因式分解法:因式分解法就是借助因式分解求出方程的解的办法,这种办法方便易用,是解一元二次方程最常见的办法.
【变式3-2】(2019•扬州)一元二次方程x(x﹣2)=x﹣2的根是____________________.
【答案】x1=2,x2=1.
【分析】x(x﹣2)=x﹣2,
x(x﹣2)﹣(x﹣2)=0,
(x﹣2)(x﹣1)=0,
x﹣2=0,x﹣1=0,
x1=2,x2=1,
故答案为:x1=2,x2=1.
点睛:本题考查知道一元二次方程的应用,能把一元二次方程转化成一元一次方程是解此题的重点.
【考试知识点4】一元二次方程的辨别式问题
【例4】(2019•铁岭)若关于x的一元二次方程ax2﹣8x+4=0有两个不相等的实数根,则a的取值范围是__________.
【答案】a<4且a≠0
【分析】由题意可知:△=64﹣16a>0,
∴a<4,
∵a≠0,
∴a<4且a≠0,
故答案为:a<4且a≠0
点睛:本题考查根的辨别式,解题的重点是熟练运用根的辨别式,本题是基础题型.
【变式4-1】(2019•宁夏)已知一元二次方程3x2+4x﹣k=0有两个不相等的实数根,则k的取值范围____________________.
【答案】k![]() .
.
【分析】∵方程3x2+4x﹣k=0有两个不相等的实数根,
∴△>0,即42﹣4×3×(﹣k)>0,
解得k![]() ,
,
故答案为:k![]() .
.
点睛:本题考查根的辨别式,总结:一元二次方程根的状况与辨别式△的关系:(1)△>0⇔方程有两个不相等的实数根;(2)△=0⇔方程有两个相等的实数根;(3)△<0⇔方程没实数根.
【变式4-2】(2019•黄石)已知关于x的一元二次方程x2﹣6x+(4m+1)=0有实数根.
(1)求m的取值范围;
(2)若该方程的两个实数根为x1、x2,且|x1﹣x2|=4,求m的值.
【分析】(1)∵关于x的一元二次方程x2﹣6x+(4m+1)=0有实数根,
∴△=(﹣6)2﹣4×1×(4m+1)≥0,
解得:m≤2.
(2)∵方程x2﹣6x+(4m+1)=0的两个实数根为x1、x2,
∴x1+x2=6,x1x2=4m+1,
∴(x1﹣x2)2=(x1+x2)2﹣4x1x2=42,即32﹣16m=16,
解得:m=1.
点睛:本题考查了根与系数的关系与根的辨别式,解题的重点是:(1)牢记“当△≥0时,方程有实数根”;(2)借助根与系数的关系结合|x1﹣x2|=4,找出关于m的一元一次方程.
【考试知识点5】一元二次方程的根与系数的关系问题
【例5】(2019•十堰)已知于x的元二次方程x2﹣6x+2a+5=0有两个不相等的实数根x1,x2.
(1)求a的取值范围;
(2)若x12+x22﹣x1x2≤30,且a为整数,求a的值.
【答案】 a<2; ﹣1,0,1.
【分析】(1)∵关于x的一元二次方程x2﹣6x+2a+5=0有两个不相等的实数根x1,x2,
∴△>0,即(﹣6)2﹣4(2a+5)>0,
解得a<2;
(2)由根与系数的关系知:x1+x2=6,x1x2=2a+5,
∵x1,x2满足x12+x22﹣x1x2≤30,
∴(x1+x2)2﹣3x1x2≤30,
∴36﹣3(2a+5)≤30,
∴a![]() ,∵a为整数,
,∵a为整数,
∴a的值为﹣1,0,1.
点睛:本题主要考查根与系数的关系及根的辨别式,借助根的辨别式求得k的取值范围是解题的重点,注意方程根的概念的运用.
【变式5-1】(2019•绥化)已知关于x的方程kx2﹣3x+1=0有实数根.
(1)求k的取值范围;
(2)若该方程有两个实数根,分别为x1和x2,当x1+x2+x1x2=4时,求k的值.
【答案】 k的取值范围为k![]()
k的值为1.
【分析】(1)当k=0时,原方程为﹣3x+1=0,
解得:x![]() ,
,
∴k=0符合题意;
当k≠0时,原方程为一元二次方程,
∵该一元二次方程有实数根,
∴△=(﹣3)2﹣4×k×1≥0,
解得:k![]() .
.
综上所述,k的取值范围为k![]() .
.
(2)∵x1和x2是方程kx2﹣3x+1=0的两个根,
∴x1+x2![]() ,x1x2
,x1x2![]() .
.
∵x1+x2+x1x2=4,
∴![]() 4,
4,
解得:k=1,
经检验,k=1是分式方程的解,且符合题意.
∴k的值为1.
点睛:本题考查了根的辨别式、根与系数的关系、一元二次方程的概念、解一元一次方程与解分式方程,解题的重点是:(1)分k=0及k≠0两种状况,找出k的取值范围;(2)借助根与系数的关系结合x1+x2+x1x2=4,找出关于k的分式方程.
【考试知识点6】一元二次方程的增长率问题
【例6】(2019•大连)某村2016年的人均收入为20000元,2018年的人均收入为24200元
(1)求2016年到2018年该村人均收入的年平均增长率;
(2)假设2019年该村人均收入的增长率与前两年的年平均增长率相同,请你预测2019年村该村的人均收入是多少元?
【答案】 2016年到2018年该村人均收入的年平均增长率为10%
预测2019年村该村的人均收入是26620元
【分析】(1)设2016年到2018年该村人均收入的年平均增长率为x,
依据题意得:20000(1+x)2=24200,
解得:x1=0.1=10%,x2=﹣2.1(不合题意,舍去).
答:2016年到2018年该村人均收入的年平均增长率为10%.
(2)24200×(1+10%)=26620(元).
答:预测2019年村该村的人均收入是26620元.
点睛:本题考查了一元二次方程的应用,解题的重点是:(1)找准等量关系,正确列出一元二次方程;(2)依据数目关系,列式计算.
【变式6-1】(2019•贺州)2016年,某贫困户的家庭年人均纯收入为2500元,通过政府产业扶持,进步了养殖业后,到2018年,家庭年人均纯收入达到了3600元.
(1)求该贫困户2016年到2018年家庭年人均纯收入的年平均增长率;
(2)若年平均增长率维持不变,2019年该贫困户的家庭年人均纯收入是不是能达到4200元?
【答案】 该贫困户2016年到2018年家庭年人均纯收入的年平均增长率为20%
2019年该贫困户的家庭年人均纯收入能达到4200元
【分析】(1)设该贫困户2016年到2018年家庭年人均纯收入的年平均增长率为x,
依题意,得:2500(1+x)2=3600,
解得:x1=0.2=20%,x2=﹣2.2(舍去).
答:该贫困户2016年到2018年家庭年人均纯收入的年平均增长率为20%.
(2)3600×(1+20%)=4320(元),
4320>4200.
答:2019年该贫困户的家庭年人均纯收入能达到4200元.
点睛:本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的重点.
【考试知识点7】一元二次方程的面积问题
【例7】(2019•徐州)如图,有一块矩形硬纸板,长30cm,宽20cm.在其四角各剪去一个同样的正方形,然后将四周突出部分折起,可制成一个无盖长方体盒子.当剪去正方形的边长取何值时,所得长方体盒子的侧面积为200cm2?

【答案】当剪去正方形的边长为![]() cm时,所得长方体盒子的侧面积为200cm2.
cm时,所得长方体盒子的侧面积为200cm2.
【分析】设剪去正方形的边长为xcm,则做成无盖长方体盒子的底面长为(30﹣2x)cm,宽为(20﹣2x)cm,高为xcm,
依题意,得:2×[(30﹣2x)+(20﹣2x)]x=200,
整理,得:2x2﹣25x+50=0,
解得:x1![]() ,x2=10.
,x2=10.
当x=10时,20﹣2x=0,不合题意,舍去.
答:当剪去正方形的边长为![]() cm时,所得长方体盒子的侧面积为200cm2.
cm时,所得长方体盒子的侧面积为200cm2.
点睛:本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的重点.
【变式7-1】(2019•襄阳)改变小区环境,争创文明家园.如图所示,某社区决定在一块长(AD)16m,宽(AB)9m的矩形场地ABCD上修建三条同样宽的小路,其中两条与AB平行,另一条与AD平行,其余部分种草.要使草坪部分的总面积为112m2,则小路的宽应为多少?
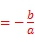
【答案】小路的宽应为1m.
【分析】设小路的宽应为xm,
依据题意得:(16﹣2x)(9﹣x)=112,
解得:x1=1,x2=16.
∵16>9,
∴x=16不符合题意,舍去,
∴x=1.
答:小路的宽应为1m.
点睛:本题考查一元二次方程的应用,弄清“草坪的总长度和总宽度”是解决本题的重点.
【考试知识点8】一元二次方程的销售问题
【例8】(2019•东营)为加快新旧动能转换,提升公司经济效益,某公司决定对最近研发出的一种电子商品进行降价营销,使生产的电子商品可以准时售出,依据市场调查:这种电子商品销售单价定为200元时,天天可售出300个;若销售单价每减少1元,天天可多售出5个.已知每一个电子商品的固定本钱为100元,问这种电子商品降价后的销售单价为多少元时,公司天天可获利32000元?
【答案】这种电子商品降价后的销售单价为180元时,公司天天可获利32000元.
【分析】设降价后的销售单价为x元,则降价后天天可售出[300+5(200﹣x)]个,
依题意,得:(x﹣100)[300+5(200﹣x)]=32000,
整理,得:x2﹣360x+32400=0,
解得:x1=x2=180.
180<200,符合题意.
答:这种电子商品降价后的销售单价为180元时,公司天天可获利32000元.
点睛:本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的重点.
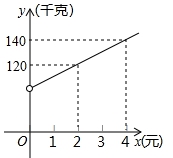
【变式8-1】(2019•安顺)安顺某商贸公司以每千克40元的价格购进一种干果,计划以每千克60元的价格销售,为了让客户得到更大的便宜,现决定降价销售,已知这种干果销量y(千克)与每千克降价x(元)(0<x<20)之间满足一次函数关系,其图象如图所示:
(1)求y与x之间的函数关系式;
(2)商贸公司要想获利2090元,则这种干果每千克应降价多少元?
【答案】商贸公司要想获利2090元,则这种干果每千克应降价9元.
【分析】(1)设一次函数分析式为:y=kx+b
当x=2,y=120;当x=4,y=140;
∴![]() ,
,
解得:![]() ,
,
∴y与x之间的函数关系式为y=10x+100;
(2)由题意得:
(60﹣40﹣x)(10 x+100)=2090,
整理得:x2﹣10x+9=0,
解得:x1=1.x2=9,
∵让客户得到更大的便宜,
∴x=9,
答:商贸公司要想获利2090元,则这种干果每千克应降价9元.
点睛:本题考查了一元二次方程的应用、一次函数的应用;由题意列出方程组或方程是解题的重点.
![]()
1.(2019•滨州)用配办法解一元二次方程x2﹣4x+1=0时,下列变形正确的是()
A.(x﹣2)2=1 B.(x﹣2)2=5 C.(x+2)2=3 D.(x﹣2)2=3
【答案】D
【分析】x2﹣4x+1=0,
x2﹣4x=﹣1,
x2﹣4x+4=﹣1+4,
(x﹣2)2=3,
故选:D.
点睛:本题考查知道一元二次方程,能正确配方是解此题的重点.
2.(2019•营口)若关于x的方程kx2﹣x![]() 0有实数根,则实数k的取值范围是()
0有实数根,则实数k的取值范围是()
A.k=0 B.k![]() 且k≠0 C.k
且k≠0 C.k![]() D.k
D.k![]()
【答案】C
【分析】当k≠0时,△=1+4k![]() 1+3k≥0,
1+3k≥0,
∴k![]() ,
,
∴k![]() 且k≠0,
且k≠0,
当k=0时,
此时方程为﹣x![]() 0,满足题意,
0,满足题意,
故选:C.
点睛:本题考查一元二次方程,解题的重点是正确理解根的辨别式,本题是基础题型.
3.(2019•丹东)等腰三角形一边长为2,它的另外两条边的长度是关于x的一元二次方程x2﹣6x+k=0的两个实数根,则k的值是()
A.8 B.9 C.8或9 D.12
【答案】B
【分析】当等腰三角形的底边为2时,
此时关于x的一元二次方程x2﹣6x+k=0的有两个相等实数根,
∴△=36﹣4k=0,
∴k=9,
此时两腰长为3,
∵2+3>3,
∴k=9满足题意,
当等腰三角形的腰长为2时,
此时x=2是方程x2﹣6x+k=0的其中一根,
∴4﹣12+k=0,
∴k=8,
此时另外一根为:x=4,
∵2+2=4,
∴不可以组成三角形,
综上所述,k=9,
故选:B.
点睛:本题考查一元二次方程,解题的重点是熟练运用一元二次方程的解法与等腰三角形的性质,本题是中等题型.
4.(2019•包头)已知等腰三角形的三边长分别为a、b、4,且a、b是关于x的一元二次方程x2﹣12x+m+2=0的两根,则m的值是()
A.34 B.30 C.30或34 D.30或36
【答案】A
【分析】当a=4时,b<8,
∵a、b是关于x的一元二次方程x2﹣12x+m+2=0的两根,
∴4+b=12,
∴b=8不符合;
当b=4时,a<8,
∵a、b是关于x的一元二次方程x2﹣12x+m+2=0的两根,
∴4+a=12,
∴a=8不符合;
当a=b时,
∵a、b是关于x的一元二次方程x2﹣12x+m+2=0的两根,
∴12=2a=2b,
∴a=b=6,
∴m+2=36,
∴m=34;
故选:A.
点睛:本题考查一元二次方程根与系数的关系;依据等腰三角形的性质进行分类讨论,结合韦达定理和三角形三边关系进行解题是重点.
5.(2019•荆州)若一次函数y=kx+b的图象不经过第二象限,则关于x的方程x2+kx+b=0的根的状况是()
A.有两个不相等的实数根 B.有两个相等的实数根
C.无实数根 D.没办法确定
【答案】A
【分析】∵一次函数y=kx+b的图象不经过第二象限,
∴k>0,b≤0,
∴△=k2﹣4b>0,
∴方程有两个不相等的实数根.
故选:A.
点睛:本题考查了根的辨别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2﹣4ac有如下关系:当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程无实数根.也考查了一次函数的性质.
6.(2019•遵义)一元二次方程x2﹣3x+1=0的两个根为x1,x2,则x12+3x2+x1x2﹣2的值是()
A.10 B.9 C.8 D.7
【答案】D
【分析】∵x1为一元二次方程x2﹣3x+1=0的根,
∴x12﹣3x1+1=0,
∴x12=3x1﹣1,
∴x12+3x2+x1x2﹣2=3x1﹣1+3x2+x1x2﹣2=3(x1+x2)+x1x2﹣3,
依据题意得x1+x2=3,x1x2=1,
∴x12+3x2+x1x2﹣2=3×3+1﹣3=7.
故选:D.
点睛:本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2![]() ,x1x2
,x1x2![]() .
.
7.(2019•鸡西)某校“研学”活动小组在一次野外实践时,发现一种植物的主干长出若干数目的支干,每一个支干又长出同样数目的小分支,主干、支干和小分支的总数是43,则这种植物每一个支干长出的小分支个数是()
A.4 B.5 C.6 D.7
【答案】C
【分析】设这种植物每一个支干长出x个小分支,
依题意,得:1+x+x2=43,
解得:x1=﹣7(舍去),x2=6.
故选:C.
点睛:本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的重点.
8.(2019•朝阳)一元二次方程x2﹣x﹣1=0的根的状况是()
A.有两个不相等的实数根 B.有两个相等的实数根
C.没实数根 D.没办法判断
【答案】A
【分析】∵△=(﹣1)2﹣4×(﹣1)=5>0,
∴方程有两个不相等的两个实数根.
故选:A.
点睛:本题考查了根的辨别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2﹣4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.
9.(2019•湘潭)已知关于x的一元二次方程x2﹣4x+c=0有两个相等的实数根,则c=()
A.4 B.2 C.1 D.﹣4
【答案】A
【分析】∵方程x2﹣4x+c=0有两个相等的实数根,
∴△=(﹣4)2﹣4×1×c=16﹣4c=0,
解得:c=4.
故选:A.
点睛:本题考查了根的辨别式与解一元一次方程,由方程有两个相等的实数根结合根的辨别式得出关于c的一元一次方程是解题的重点.
10.(2019•资阳)a是方程2x2=x+4的一个根,则代数式4a2﹣2a的值是__________.
【答案】8
【分析】∵a是方程2x2=x+4的一个根,
∴2a2﹣a=4,
∴4a2﹣2a=2(2a2﹣a)=2×4=8.
故答案为:8.
点睛:此题主要考查了一元二次方程的解,正确将原式变形是解题重点.
11.(2019•济宁)已知x=1是方程x2+bx﹣2=0的一个根,则方程的另一个根是__________.
【答案】﹣2
【分析】∵x=1是方程x2+bx﹣2=0的一个根,
∴x1x2![]() 2,
2,
∴1×x2=﹣2,
则方程的另一个根是:﹣2,
故答案为﹣2.
点睛:此题主要考查了一元二次方程根与系数的关系,得出两根之积求出另一根是解决问题的重点.
12.(2019•抚顺)若关于x的一元二次方程kx2+2x+1=0有实数根,则k的取值范围是______________________________.
【答案】k≠0且k≤1
【分析】由题意可知:△=4﹣4k≥0,
∴k≤1,
∵k≠0,
∴k≠0且k≤1,
故答案为:k≠0且k≤1;
点睛:本题考查根的辨别式,解题的重点是熟练运用根的辨别式,本题是基础题型.
13.(2019•青海)某种药品原价每盒60元,因为医疗政策改革,价格经过两次下调后目前价格每盒48.6元,则平均每次下调的百分率为__________.
【答案】10%
【分析】设平均每次降价的百分比是x,依据题意得:
60(1﹣x)2=48.6,
解得:x1=0.1=10%,x2=1.9(不合题意,舍去),
答:平均每次降价的百分比是10%;
故答案为:10%.
点睛:本题考查了一元二次方程的应用,若设变化前的量为a,变化后的量为b,平均变化率为x,则经过两次变化后的数目关系为a(1±x)2=b.
14.某市为了扎实落实脱贫攻坚中“两不愁、三保障”的住房保障工作,去年已投入5亿元资金,并计划投入资金逐年上升,明年将投入7.2亿元资金用于保障性住房建设,则这两年投入资金的年平均增长率为__________.
【答案】20%
【分析】设这两年中投入资金的平均年增长率是x,由题意得:
5(1+x)2=7.2,
解得:x1=0.2=20%,x2=﹣2.2(不合题意舍去).
答:这两年中投入资金的平均年增长率约是20%.
故答案是:20%.
点睛:本题考查了一元二次方程中增长率的常识.增长前的量×(1+年平均增长率)年数=增长后的量.
15.(2019•呼和浩特)用配办法求一元二次方程(2x+3)(x﹣6)=16的实数根.
【答案】x1![]() ,x2
,x2![]() .
.
【分析】原方程化为一般形式为2x2﹣9x﹣34=0,
x2![]() x=17,
x=17,
x2![]() x
x![]() 17
17![]() ,
,
(x![]() )2
)2![]() ,
,
x![]() ±
±![]() ,
,
所以x1![]() ,x2
,x2![]() .
.
点睛:本题考查了一元二次方程的解法.解一元二次方程常见的办法有直接开平办法,配办法,公式法,因式分解法,要依据方程的特征灵活使用适合的办法.
16.(2019•孝感)已知关于x的一元二次方程x2﹣2(a﹣1)x+a2﹣a﹣2=0有两个不相等的实数根x1,x2.
(1)若a为正整数,求a的值;
(2)若x1,x2满足x12+x22﹣x1x2=16,求a的值.
【分析】(1)∵关于x的一元二次方程x2﹣2(a﹣1)x+a2﹣a﹣2=0有两个不相等的实数根,
∴△=[﹣2(a﹣1)]2﹣4(a2﹣a﹣2)>0,
解得:a<3,
∵a为正整数,
∴a=1,2;
(2)∵x1+x2=2(a﹣1),x1x2=a2﹣a﹣2,
∵x12+x22﹣x1x2=16,
∴(x1+x2)2﹣3x1x2=16,
∴[2(a﹣1)]2﹣3(a2﹣a﹣2)=16,
解得:a1=﹣1,a2=6,
∵a<3,
∴a=﹣1.
点睛:本题考查的是一元二次方程根与系数的关系及根的辨别式,先看出a的取值范围,再由根与系数的关系得出方程组是解答此题的重点.
17(2019•贵港)为了满足师生的阅读需要,某校图书馆的藏书从2016年底到2018年底两年内由5万册增加到7.2万册.
(1)求这两年藏书的每年平均增长率;
(2)经统计知:中外古典名著的册数在2016年底仅占当时藏书总量的5.6%,在这两年新增加的图书中,中外古典名著所占的百分率恰好等于这两年藏书的每年平均增长率,那样到2018年底中外古典名著的册数占藏书总量的百分之几?
【分析】(1)设这两年藏书的每年平均增长率是x,
5(1+x)2=7.2,
解得,x1=0.2,x2=﹣2.2(舍去),
答:这两年藏书的每年平均增长率是20%;
(2)在这两年新增加的图书中,中外古典名著有(7.2﹣5)×20%=0.44(万册),
到2018年底中外古典名著的册数占藏书总量的百分比是:![]() 100%=10%,
100%=10%,
答:到2018年底中外古典名著的册数占藏书总量的10%.
点睛:本题考查一元二次方程的应用,解答本题的重点是明确题意,列出相应的方程,借助方程的常识解答,这是一道典型的增长率问题.
18.(2019•南京)某地计划对矩形广场进行扩建改造.如图,原广场长50m,宽40m,需要扩充后的矩形广场长与宽的比为3:2.扩充地区的扩建成本每平米30元,扩建后在原广场和扩充地区都铺设地板砖,铺设地板砖成本每平米100元.假如计划总成本642000元,扩充后广场的长和宽应分别是多少米?

【分析】设扩充后广场的长为3xm,宽为2xm,
依题意得:3x•2x•100+30(3x•2x﹣50×40)=642000
解得x1=30,x2=﹣30(舍去).
所以3x=90,2x=60,
答:扩充后广场的长为90m,宽为60m.
点睛:题考查了列二元一次方程解实质问题的运用,总价=单价×数目的运用,解答时找准题目中的数目关系是重点.
19.(2019•长沙)日前,长沙教育局颁布《长沙中小学教师志愿辅导工作推行建议》,鼓励教师参与志愿辅导,某区率先示范,推出名师公益大课堂,为学生提供线上线下免费辅导,据统计,第一批公益课受益学生2万人次,第三批公益课受益学生2.42万人次.
(1)假如第二批,第三批公益课受益学生人次的增长率相同,求这个增长率;
(2)根据这个增长率,预计第四批公益课受益学生将达到多少万人次?
【分析】(1)设增长率为x,依据题意,得
2(1+x)2=2.42,
解得x1=﹣2.1(舍去),x2=0.1=10%.
答:增长率为10%.
(2)2.42(1+0.1)=2.662(万人).
答:第四批公益课受益学生将达到2.662万人次.
点睛:本题考查了一元二次方程的应用,解题重点是要了解题目的意思,依据题目给出的条件,找出适合的等量关系,列出方程,再求解.
20.(2019•衡阳)关于x的一元二次方程x2﹣3x+k=0有实数根.
(1)求k的取值范围;
(2)假如k是符合条件的最大整数,且一元二次方程(m﹣1)x2+x+m﹣3=0与方程x2﹣3x+k=0有一个相同的根,求此时m的值.
【分析】(1)依据题意得△=(﹣3)2﹣4k≥0,
解得k![]() ;
;
(2)k的最大整数为2,
方程x2﹣3x+k=0变形为x2﹣3x+2=0,解得x1=1,x2=2,
∵一元二次方程(m﹣1)x2+x+m﹣3=0与方程x2﹣3x+k=0有一个相同的根,
∴当x=1时,m﹣1+1+m﹣3=0,解得m![]() ;
;
当x=2时,4(m﹣1)+2+m﹣3=0,解得m=1,
而m﹣1≠0,
∴m的值为![]() .
.
点睛:本题考查了根的辨别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2﹣4ac有如下关系:当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程无实数根.







