小学二年级上册数学单元测试-8.数学广角---搭配(一) 人教版(2014秋)(含答案)
1、单选题
1.芳芳的父亲、母亲陪她去看电影.电影院一排有20个座位,他们要一块坐在同一排,共有()种不一样的坐法.
A. 18 ![]() B. 54
B. 54 ![]() C. 108
C. 108
2.一种变速自行车,有2个前齿轮,6个后齿轮,它能变出( )种速度。
A. 2 B. 8 C. 12 D. 6
3.用0、2、4、6可以组成没重复数字的两位数个。
A. 12 ![]() B. 9
B. 9 ![]() C. 6
C. 6
4.在一次射箭比赛中,规定每位运动员只能射3支箭,射中了哪一环就得到哪一环上相应的分数,没射中就不能分.
一位运动员用3支箭刚好射得50分的方法一共有()种.
(注意:0+0+50和0+50+O是不同的方法.)

A. 15 ![]() B. 13
B. 13 ![]() C. 16
C. 16
5.有14个篮球队进行比赛,若使用淘汰制,最后产生一名冠军,则至少要进行( )场比赛。
A. 15 B. 14 C. 13 D. 12
2、判断题
6.在一条线段上共有9个点,则这9个点可以构成38条线段。
7.假如A是奇数,那样1093+89+A+25的结果还是奇数.
8.我有2件上衣和3条裤子,配成一套衣服,一共有6种搭配办法.
3、填空题
9.梅子有2元和5元两种人民币若干张,她要拿出20元钱,有________ 种不一样的拿法.
10.用3、5、9三张卡片,每次拿两张组成一个两位数,可以组成________个不一样的两位数,其中最大的数是________,最小的数是________。
11.在7、5、1、0这四个数字中,任选三个数字组成一个三位数,这个三位数是2、3、5的公倍数,这个三位数最小是________,最大是________。
12.从班内3名男孩和4名女孩中选出2人参加羽毛球混合双打比赛,共有________种组队策略。
13.从2名男孩和5名女孩中选出一对羽毛球混合双打选手,有________种不一样的组队策略。
14.用2、5、9三张卡片中任选两张组成的数中,最大的是多少?最小的是多少?
(1)最大的数是________。
(2)最小的数是________。
4、解答卷
15.用5 1 6 三张数字卡片摆一摆,能组成几个三位数,这类三位数是2,3,5的倍数吗?请照样子在表格里填一填。

16.甲、乙、丙、丁、戊、己六个人站队,需要:甲不可以站在队伍左半边,乙不可以站在队伍右半边,丙不可以站在队伍两端,问一共有多少种站法?
5、应用题
17.A、B、C、D、E五名运动员进行乒乓球比赛,每两名运动员都要进行一场比赛,一共要进行多少场比赛?
参考答案
1、单选题
1.【答案】 C
【分析】【解答】解: ×(3+2+1)
=18×6
=108(种)
答:要让他们坐在一块,在同一排有108种不一样的坐法.
故选:C.
【剖析】把一家人看做一个整体,如此还剩20﹣3+1=18个座位,因此有18种选择,又由于一家3人的地方可以交换,又有3+2+1=6种选择,所以共有18×6=108(种);据此解答.
2.【答案】 C
【分析】【解答】解:这个变速自行车能变出2×6=12种速度。
故答案为:C。
【剖析】由于这个变速自行车有2个前齿轮和6个后齿轮,所以1个前齿轮能搭配6种后齿轮,2个前齿轮能搭配2×6=12种后齿轮。
3.【答案】 B
【分析】【解答】解:可以组成的两位数有20、24、26、40、42、46、60、62、64,共9个。
故答案为:B。
【剖析】0不可以作为最高位数字,2、 4、6都可以作为十位数字,先确定十位数字,再确定个位数字,写出所有数字再确定个数即可。
4.【答案】 A
【分析】【解答】解:①射中0、0、50环:有3种,
②射中20、20、10环:有3种,
③射中10、10、30环:有3种,
④射中30、0、20环:有6种,
共有:3+3+3+6=15(种);
答:一共有15种.
故选:A.
【剖析】由于50=0+0+50=20+20+10=10+10+20=30+20+0,所以分4种状况排列即可.
5.【答案】 C
【分析】【解答】解:14-1=13(场)
故答案为:C。
【剖析】此题可以直接用14-1算出,由于每场都要淘汰一个队,到最后一场肯定有一个胜出,没淘汰的队,所以可以直接算出。
2、判断题
6.【答案】 错误
【分析】【解答】解:8+7+6+5+4+3+2+1=36(条),原题说法错误。
故答案为:错误。
【剖析】从第一个点可以引出8条线段,第二个点可以引出7条不重复的线段,……,倒数第二个点可以引出1条不重复的线段,把这类线段条数相加就是构成线段的总条数。
7.【答案】错误
【分析】【解答】解:假如A是奇数,
1093+89+A+25为求四个奇数数相加的和,
偶数个奇数相加的和为偶数,
所以其和肯定为偶数.
故答案为:错误.
【剖析】依据数和的奇偶性可知,奇数个奇数相加的和为奇数,偶数个奇数相加的和为偶数.式中1093、89、25均为奇数,假如A也为奇数的话,则为四个奇数相加,其和肯定为偶数.
8.【答案】 正确
【分析】【解答】解:2×3=6,所以2件上衣和3条裤子一共有6种搭配办法。原题说法正确。
故答案为:正确。
【剖析】一件上衣有3条裤子与之搭配,那样2件上衣就是2个3种搭配办法。
3、填空题
9.【答案】3
【分析】【解答】解:①10张2元
②4张5元
③2张5元和5张2元
共3种拿法.
故答案为:3.
【剖析】由于5是奇数,2是偶数,所以只能先把5元的凑成整十,才能再放2元的,故此只有3种办法.
10.【答案】 6;95;35
【分析】【解答】解:组成的两位数有35、39、53、59、93、95,共6个不一样的两位数,其中最大的数是95,最小的数是35。
故答案为:6;95;35。
【剖析】每一个数字都可以作为十位数字,然后确定个位数字,列举出所有能组成的两位数,然后判断最大的数和最小的数即可。
11.【答案】 150;750
【分析】【解答】 在7、5、1、0这四个数字中,任选三个数字组成一个三位数,这个三位数是2、3、5的公倍数,这个三位数最小是150,最大是750。
故答案为:150;750。
【剖析】此题主要考查了2、3、5的倍数的特点,同时是2、3、5的倍数的最小的三位数,只须个位是0,百位是最小的自然数1,十位满足和百位、个位上的数加起来是3的倍数即可;需要最大是多少,只须个位是0,十位和百位的数加起来是3的倍数即可,据此解答。
12.【答案】12
【分析】【解答】解:3×4=12(种);
故答案为:12.
【剖析】3名男孩和4名女孩选出一对乒乓球混合双打选手,则每一名男孩都可和四名不一样的女孩搭配,依据乘法原理可知,共有3×4=12种不一样的组队策略.
13.【答案】10
【分析】【解答】解:2×5=10(种)
故答案为:10.
【剖析】每名男孩与女孩组队时,都有5种不一样的组队策略,所以直接用2乘5即可求出组队的总策略。
14.【答案】 (1)95
(2)25
【分析】【解答】2、5、9三张数字卡片,任选两张,可组成的数字为25、29、52、59、92、95,共6种。其中,最大的数是95,最小的数是25。
4、解答卷
15.【答案】 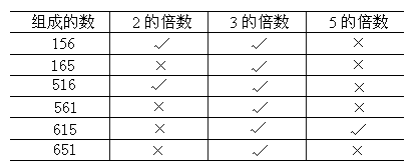
【分析】【解答】解:用5、1、6组成的三位数有:156、165、516、561、615、651

【剖析】依据排列组合的办法,找出5、1、6所组成的所有三位数,再依据2、3、5的倍数特点进行解答即可。
16.【答案】 解:先对丙定位,有4种站法,无论丙站在哪儿,甲和乙肯定有一个人有两种站法,一个人有三种站法,剩下三个人进行全排列,所以站法总数有: ![]() (种).
(种).
【分析】【解答】解:4×3×2×![]() =144(种)
=144(种)
答:一共有144种站法。
【剖析】丙不可以站在队伍两端,那样丙有4种站法,故甲和乙肯定有一个人有两种站法,一个人有三种站法,剩下三个人进行全排列即可。
5、应用题
17.【答案】 10场
【分析】【解答】解:4+3+2+1=10(场)
答:一共要进行10场比赛。
【剖析】A与B、C、D、E各进行一场,共4场;B与剩下的C、D、E共进行3场;C与剩下的D、E共进行2场;D与剩下的E进行1场,把所有些场次相加就是比赛总场次。







