2019年人教版数学高中一年级上学期综合测试卷三
第I卷（选择题）
1、选择题（本大题共12小题，每小题4分，共48分）
1．下列函数中与函数
相同的一个是（ ）
A．
B．
C．
D
．
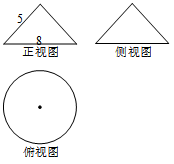
2．若某几何体的三视图如图所示，其中正视图与侧视图是两个全等的等腰三角形，则此几何体的表面积是（ ）
A．
B． C．
D．
3．设
，
是两条不一样的直线，
，是两个不一样的平面，则（ ）
A．若
，
，则
B．若，，则
C．若
，
，则 D．若，
，则
4．三棱锥
的三条侧棱两两互相垂直，且长度分别为1、
、3，则这个三棱锥的外接球的表面积为（ ）
A． B．
C．
D．
5．圆的圆心坐标和半径分别为（ ）
A．（0,2），2 B．（2,0），2 C．（-2,0），4 D．（2,0），4
6．给定下列四个命题：
①若一个平面内的两条直线与另一个平面都平行，那样这两个平面相互平行；
②若一个平面经过另一个平面的垂线，那样这两个平面相互垂直；
③垂直于同一直线的两条直线相互平行；
④若两个平面垂直，那样一个平面内与它们的交线不垂直的直线与另一个平面也不垂直．
其中，为真命题的是
A. ①和② B. ②和③ C. ③和④ D. ②和④
7．直线
的倾斜角是（ ）
A.
B. C.
D.
8．若两平行直线：与：
之间的距离是
，则
（ ）
A． B．
C．
D．
9．过点，
的直线的斜率为
，则（ ）
A．
B． C． D．
10．已知点
，则线段
的垂直平分线的方程是．
A． B． C．
D．
11．正方体
中直线与平面
所成角的余弦值是（ ）
A.
B. C.
D.
12．函数的零点所在区间为（ ）
A． B． C．
D．
第II卷（非选择题）
2、填空题（本大题共4小题，每小题4分，共16分）
13．设
为概念在
上的奇函数，当时，，则=__________．
14．已知直线，若直线
与直线
垂直，则的值为__________．
15．过点且在坐标轴上截距相等的直线方程为__________．
16．一个正方体纸盒展开后如图所示，在原正方体纸盒中有如下结论：
①AB⊥EF；
②AB与CM所成的角为60°；
③EF与MN是异面直线；
④MN∥CD．
以上四个命题中，正确命题的序号是 ____________________
3、解答卷（本大题共5大题，共56分）
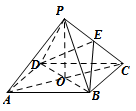17．（满分10分）如图，是正方形，是该正方形的中心，是平面外一点，
平面，
是
的中点.
（1）求证：//平面
（2）求证：平面.
18．（满分10分）已知的三个顶点分别为，求：
（1）边所在直线的方程；
（2）边上中线所在直线的方程.
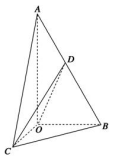19．（满分12分）如图所示，在三棱锥中，⊥底面
，∠
＝∠＝30°，＝
＝4，
＝，动点
在线段上.
（1）求证：平面⊥平面
；
（2）当⊥时，求三棱锥的体积.
20.（满分12分）求经过坐标原点和点，并且圆心在直线上的圆
的方程.
21．（满分12分）已知圆方程
.
（1）求的取值范围；
（2）若圆与直线相交于两点，且（为坐标原点）， 求的值；
（3）在（2）的条件下，求以为直径的圆的方程.
参考答案
1．C 2．A 3．C 4．A 5．B 6．D 7．B 8．C 9．D 10．B 11．C 12．C
13． 14．0或2 15．2x-y=0或x+y-3=0 16．①③
17．证明：（1）连接，∵四边形为正方形，
∴为的中点，
∵是的中点，∴是的中位线……………2分
∴
，∵
平面，平面，
∴平面…………………………………………5分
（2）∵平面，平面，
∴，………………………………………….…6分
∵四边形是正方形，
∴，………………………………………….…7分
∵，平面，平面，
∴
平面…………………………………….…10分
18．解：（1）直线经过和两点，
由两点式得的方程为，
即………………………………………….5分
（2）易得边的中点的坐标为
，
边的中线过点两点，
由截距式得所在直线方程为
，
即……………………………………….10分
19．解：（1）∵AO⊥底面BOC，
∴AO⊥OC， AO⊥OB………………………………… 2分
∵∠OAB＝∠OAC＝30°，AB＝AC＝4，
∴OC＝OB＝2. 又BC＝2
， ∴OC⊥OB，
∴OC⊥平面AOB…………………………………………4分
∵OC平面COD，
∴平面COD⊥平面AOB………………………………….6分
（2）∵OD⊥AB，∴BD＝1，OD＝.
∴VC－OBD ＝ 
×
××1×2＝ …….12分
20．解：显然，所求圆的圆心在OP的垂直平分线上，OP的垂直平分线方程为：
，即x＋y－1＝0…………………3分
解方程组，得圆心C的坐标为（4，－3）………8分
又圆的半径r＝|OC|＝5，…………………………………………..10分
∴所求圆的方程为（x－4）2＋（y＋3）2＝25. …………………..12分
21．解：
（1）由 得:
………………4分
（2）由题意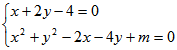
把代入
得
，
∵得出：
∴
∴ ………………………………………………8分
（3）设圆心为
半径
圆的方程 ………………12分
