《4.6 用尺规作线段与角》基础训练
1. 下列尺规作图的语句正确的是.
A.延长射线AB到点C
B.延长直线AB到点C
C.延长线段AB到点C,使BC=AB
D.延长线段AB到点C,使AC=BC
2. 画一个钝角∠AOB,然后以O为顶点,以OA为一边,在角的内部画一条射线OC,使∠AOC=90°,正确的图形是.

3. 下列尺规作图的语句错误的是.
A.作∠AOB,使∠AOB=3∠1
B.以点O为圆心作弧
C.以点A为圆心,线段a的长为半径作弧
D.作∠ABC,使∠ABC=∠1+∠2
4. 下列各选项中,只用没刻度的直尺就能作出图形的是.
A.作线段AB=a
B.过O、P作射线OP
C.在直线AB上截取线段AC=a
D.在射线OA上截取线段OB=a
5. 下列画图是尺规作图的是.
A.用量角器画出∠AOB的平分线
B.不需要量角器,作∠AOB,使∠AOB=3∠1
C.用三角板画∠AOB=90°
D.画线段AB=3 cm
6. 下列说法正确的有.
①借助尺规能作一个角等于已知角;②借助尺规能作一个角等于已知两个角的和;③借助尺规能作一个角等于已知两个角的差;④借助尺规不可以作一个角等于已知角的2倍.
A.1个 B.2个 C.3个 D.4个
7. 如图①,已知线段a和线段b,则AE表示的是.

图①
A.3 B.3a-b C.2a D.2a+b
8. 尺规作图是指.
A.用直尺规范作图 B.用刻度尺和圆规作图
C.用没刻度的直尺和圆规作图 D.直尺和圆规是作图工具
9. 下列各选项中,只用圆规就能作出图形的是.
A.过点O、A作直线OA
B.作一个角等于已知角
C.在射线OA上截取线段OB=a
D.作一条线段等于已知线段
10. 如图②,点C在∠AOB的边OB上,用尺规作出了∠BCN=∠AOC,作图痕迹中,弧FG是.

图②
A.以点C为圆心,OD长为半径所画的弧
B.以点C为圆心,DM长为半径所画的弧
C.以点E为圆心,OD长为半径所画的弧
D.以点E为圆心,DM长为半径所画的弧
11. 如图③,尺规作图:已知线段AB,延长线段AB到C,使BC=2AB.
![]()
图③
12. 如图④,已知线段a和两条互相垂直的直线AB,CD. 求作正方形A′B′C′D′,使其对角线长等于2a.
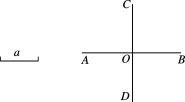
图④
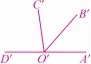
13. 如图⑤,已知∠α,∠AOB=90°,求作∠AOC,使其等于∠α的余角.

图⑤
14. 已知,如图⑥,三条线段a, b,c.请画线段AB,使AB=a+b+c.
![]()
图⑥
15. 已知线段a,如图:![]() .求作:线段AB,使AB=3a.
.求作:线段AB,使AB=3a.
答案和分析
【答案】
1. C 2. D 3. B 4. B 5. B
6. C 7. B 8. C 9. C 10. D
11. 见答案. 12. 见答案. 13. 见答案.
14. 见答案. 15. 见答案.
【分析】
1. 解:射线旁边是无限延伸的,只能反向延长,A错误;
直线是无限延伸的,不需要延长,B错误;
延长线段AB到点C,不可能使得AC=BC,D错误,
故选C.
解题的重点在于对有关定义的理解.
2. 解:因为∠AOC=90°,则B、C错误;
由于射线OC在∠AOB的内部,则A错误,D正确,
故选D.
解题的重点在于对角的有关定义的理解.
3. 解:在描述作弧时,要给出圆心和半径,故B错误,
故选B.
解题的重点在于对尺规作图的有关语句的理解.
4. 解:没刻度的直尺不可以作出与已知线段长度相等的线段,故A、C、D错误,
但可作出射线,D正确.
故选B.
只用没刻度的直尺不可以作出与已知线段长度相等的线段,但可直接作出直线或射线.
5. 解:A中借用于量角器,C中借用于三角板,D中借用于刻度尺,B不需要量角器,用没刻度的直尺和圆规完成即可,
故选B.
一般用没刻度的直尺和圆规来画图,这种画图的办法叫做尺规作图.
6. 解:可以用尺规作图的有:①作一个角等于已知角;②作一个角等于已知两个角的和;③作一个角等于已知两个角的差;④作一个角等于已知角的2倍,
故正确的有①②③,共3个,
故选C.
一般用没刻度的直尺和圆规来画图,这种画图的办法叫做尺规作图.可以用尺规作出已知角的和、差、倍数.
7. 解:已知线段a和线段b,则AE表示的是3a-b.
故选B.
此题考查的是对尺规作图的认识,解答此题的重点是能灵活运用线段的和、差转化线段之间的数目关系.
8. 解:尺规作图是指用没刻度的直尺和圆规作图,
故选C.
此题考查的是尺规作图的概念,一般用没刻度的直尺和圆规来画图,这种画图的办法叫做尺规作图.
9. 解:只用圆规就能作出图形的是在射线OA上截取线段OB=a,
而A、B、D都需要用尺规进行作图,
故选C.
一般用没刻度的直尺和圆规来画图,这种画图的办法叫做尺规作图.解题重点是理解只用圆规就能在射线上截取线段.
10. 解:由图可知,弧FG是以点E为圆心,DM长为半径所画的弧,
故选D.
本题主要考查了基本作图,解题重点是理解作图的每一步所代表的意义.
11. 解:如图⑦所示,AC即为所求.
![]()
图⑦
借助作线段的办法求解即可.
本题主要考查了基本作图,解题的重点是正确用尺规完成作图.
12. 解:作法:借助圆规,在射线OA,OB,OC,OD上作线段OA′,OB′,OC′,OD′,使它们分别与线段a相等.
依次连接A′,C′,B′,D′,A′.

此题主要考查了基本作图,学会正方形的性质是解题的重点.
13. 解:如图⑧所示,∠AOC就是所求的角.
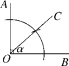
图⑧
以OB为一边作∠BOC=∠α,则∠AOC就是所求.
本题考查了基本作图,作一个角等于已知角,与余角的概念,解题时要灵活运用.
14. 解:如图⑨所示,AB即为所求.
![]()
图⑨
依据三条线 a,b,c,分别在射线上截取,得出AB即可.
此题主要考查了基本作图,在解答此类问题时必须要注意各点之间的关系.
15. 解:作法:作射线AE;在射线AE上顺次截取AC=CD=DB=a,则线段AB即为所求作的线段.
![]()
借助作线段的办法求解即可.
本题主要考查了基本作图,解题的重点是正确用尺规完成作图.
《4.6 用尺规作线段与角》提升训练
1. 如图①,在直线AB上找出一点C,使AC=2CB,则C点应在.
![]()
图①
A. 点A、B之间
B.点A的左侧
C.点B的右侧
D.点A、B之间或点B的右侧
2. 如图②,画线段AB;延长线段AB到点C,使BC=2AB;反向延长AB到点D,使AD=AC,则线段CD=AB.
![]()
图②
A.6 B.4 C.5 D.7
3. 下列是尺规作图的是.
A.用量角器画∠AOB的平分线OP
B.借助两块三角板画15°的角
C.用刻度尺测量后画线段AB=10 cm
D.在射线OP上截取OA=AB=BC=a
4. 下列关于作图的语句正确的是.
A.作∠AOB的平分线OE=3 cm
B.画直线AB=线段CD
C.用直尺作三角形的高是尺规作图
D.已知A、B、C三点,过这三点未必能画出一条直线
5. 如图③,已知线段a,b,c,求作线段AB,使AB=a+c-b.

图③
6. 已知:如图④,有线段m,n,画一条线段AB,使它等于2m+n.
![]()
图④
7. 如图⑤,已知∠1,∠2,且∠1>∠2,用尺规作∠AOB,使得:
∠AOB=∠1+∠2;
∠AOB=2∠1-∠2.

图⑤
8. 已知:如图⑥,锐角∠AOB,求作:∠β,使得∠β=180°-2∠AOB.
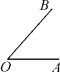
图⑥
9. 如图⑦,已知线段a、b、c,用圆规和直尺画线段,使它等于2a+b-c.
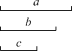
图⑦
10. 如图⑧,已知∠α和∠β,求作∠AOB,使∠AOB=∠α-∠β.
![]()
图⑧
答案和分析
【答案】
1. D 2. A 3. D 4. D 5. 见答案.
6. 见答案. 7. 见答案. 8. 见答案.
9. 见答案. 10. 见答案.
【分析】
1. 解:在直线AB上找出一点C,使AC=2CB,则C点应在点A、B之间或点B的右侧,
故选D.
点C的存在有两种状况: C点在点A、B之间; C点在点B的右侧.
2. 解:由图可知,BC=2AB,则AC=AB+BC=AB+2AB=3AB,
由于AD=AC,所以CD=AD+AC=2AC=6AB,
故选A.
此题考查的是对尺规作图的认识,解答此题的重点是能灵活运用线段的和、差转化线段之间的数目关系.
3. 解:A中借用于量角器,B中借用于三角板,C中借用于刻度尺,D中用没刻度的直尺和圆规完成即可,
故选D.
此题考查的是尺规作图的概念,一般用没刻度的直尺和圆规来画图,这种画图的办法叫做尺规作图.
4. 解:射线、直线具备延伸性,不可以画出其长度,故A、B错误;
尺规作图需用圆规和无刻度的直尺,故C错误;
若A、B、C三点不共线,则没办法过这三点画出一条直线,故D正确.
故选D.
解题的重点是学会尺规作图的概念和射线、直线的有关常识.
5. 解:作法:作射线AC;
在射线AC上依次截取AD=a,DE=c,得线段AE;
在线段AE上,以E为端点,截取EB=b,则线段AB即为所求作的图形.
![]()
此题主要考查了基本作图,在解答此类问题时必须要注意线段之间的和差关系.
6. 解:画射线AM,并在射线AM上顺次截取AC=CD=m,DB=n.则线段AB就是所求作的线段.
![]()
本题考查了基本作图,学会作一条线段等于已知线段,与线段的和、差、倍的意义是解题重点.
7. 解:如图①所示,∠AOB即为所求;
如图②所示,∠AOB即为所求.
本题考查了基本作图,学会作一个角等于已知角,与角的和、差、倍的意义是解题重点.
8. 解:作法:作∠A′O′B′=∠AOB;
以O′B′为始边作∠B′O′C′=∠AOB;
反向延长射线O′A′到D′,∠β为图中所示的∠C′O′D′.
本题考查了基本作图,作一个角等于已知角,与平角的概念,解题时要灵活运用.
9. 解:作法:作射线AF;
在射线AF上顺次截取AB=BC=a,CD=b ;
在线段AD上截取DE=c.所以线段AE即为所求.
![]()
对于比较复杂的尺规作图,可先画出草图,找到正确作图办法.
10. 解:作法:作射线OA;
以射线OA为一边作∠AOC=∠α;
以O为顶点,以射线OC为一边,在∠AOC的内部作∠BOC=∠β,则∠AOB就是所求
作的角.

本题考查了基本作图,学会作一个角等于已知角,与角的和差的意义是解题重点.
《4.6 用尺规作线段与角》培优训练
1. 下列画图语言表述正确的是.
A.延长线段AB至点C,使AB=AC
B.以点O为圆心作弧
C.以点O为圆心,以AC长为半径画弧
D.在射线OA上截取OB=a,BC=b,则有OC=a+b
2. 如图所示,已知线段a,b,c.
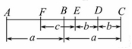
3. 如图①,用a,b,c表示线段AF的长应为.
![]()
图①
A. 2a-2b-c B. 2a-b-c
C. 2a-b-c D. 2a-2b+c
4. 如图②,已知线段a ,b,画一条线段,使它等于2a-b.
![]()
图②
5. 如图③,已知:∠1,∠2,求作:∠3,使得∠3=∠2-∠1;∠4,使得∠4=∠1+5∠2.
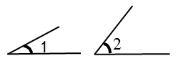
图③
答案和分析
【答案】
1. C 2. D 3. A 4. 见答案. 5. 见答案.
【分析】
1. 解:延长线段AB至点C,则AC>AB,故A错误;
作弧要给出圆心和半径,故B错误,C正确;
在射线OA上截取OB=a,BC=b,当点C在点B的右边时,有OC=a+b,当点C在点B的左边时,OC≠a+b,故D错误,
故选C.
此题考查的是尺规作图的有关常识,解题的重点在于对尺规作图的有关语句的理解.
2. 解:用尺规先作线段AC=a,再从内部顺次截取CD=b,DB=c,则AB=a-b-c.
故选D.
此题主要考查了基本作图,在解答此类问题时必须要注意线段之间的和差关系.
3. 解:由图可知AF=AB+BC-CD-DE-EF=a+a-b-b-c=2a-2b-c.
故选A.
此题主要考查了基本作图,在解答此类问题时必须要注意线段之间的和差关系.
4. 解:作法:画射线AE;
在射线AE上顺次截取AB=BD=a;
在线段AD上截取CD=b,线段AC即为所求作的线段.
![]()
对于比较复杂的尺规作图,可先画出草图,找到正确作图办法.
5. 解:作法:①作射线OA;
②以OA为边做∠AOB=∠1;
③以O为顶点,以射线OA为边,在∠AOB内部作∠AOD=∠2.
则∠BOD即为所求的∠3.
作法:①作射线OA;
②以OA为边做∠AOB=∠1;
③以O为顶点,以射线OB为边,在∠AOB外部作∠BOD=∠2.
则∠AOD即为所求的∠3.
对于比较复杂的尺规作图,可先画出草图,找到正确作图办法.







