虹口区继光学校初三（上）首次月考试题
班级；___________ 名字；___________ 分数；___________
1、选择题.（每题4分，满分24分）
1.对一个图形进行放缩时，下列说法中正确的是（ ）
A.图形中线段的长度与角的大小都维持不变
B.图形中线段的长度可以改变，角的大小维持不变
C.图形中线段的长度维持不变，角的大小可以改变
D.图形中线段的长度与角的大小都不会改变
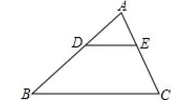
2.如图，在△ABC中，DE∥BC，AD＝4，AE＝3，CE＝6，那样AB的长是（ ）
A.4 B.6 C.8 D.12
3.假如互不相等的四条线段，a，b，c，d满足
＝
,那样下列各式中肯定成立的是（ ）
A.
＝
B.
＝
C.＝ D.
＝
4.点D，E分别是△ABC边AB，AC上的点，下列比率式中，能断定DE∥BC的是（ ）
A.＝
B.＝
C.＝
D.＝
5.如图，下列条件中，不可以断定△ACD∽△ABC的是（ ）
A.∠ADC＝∠ACB B.∠B＝∠ACD
C.∠ACD＝∠BCD D.
＝
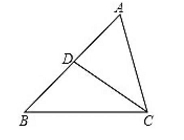
第2 题图 第5 题图
6.在Rt△ABC中，∠ACB＝90°，CD是AB边上的高，则下列结论不正确的是（ ）
A.AC²＝AD·AB B.CD²＝AD·BD
C.BC²＝AD·AB D.CD·AD＝AC·BC
第9 题图
二，填空题（每题4分，满分48分）
7.若
＝
,则
＝________
8.已知点P是线段AB上的黄金分割点，AP＞PB，AB＝10cm，则线段AP的长为_________cm
9.如图，四边形ABCD与是边长EFGH是相似图形，并且点A与点E，点B与点F，
点C与点G，点D与点H，分别是对应点，若∠A＝∠D＝100°，则∠ F＝_______
10.若△ABD∽△DEF，且相似比是2∶3.，它们的周长之和是40，则△ABC的周
长是_______
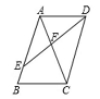
11.如图，在平行四边形ABCD中，E在AB上，AE∶EB＝2∶3，ED与AC相交于F，
则AF∶FC＝_______
12.如图，已知AD为△ABC的角平分线，DE∥AB，假如＝，那样
＝_______
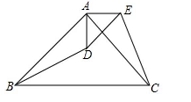
13.如图，△ABC是等腰三角形，BC是斜边。D为△ABC内一点，将△ABD绕点A逆时针旋转后与△ACE重合，假如AD＝3，那样线段DE的长等于_______
14.假如直角三角形的斜边长是18.那样这个直角三角形的重点到斜边中点的距离为_______
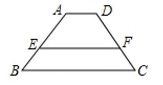
15.如图，梯形ABCD中，点E，F分别在边AB，DC上，AD∥BC∥EF,BE∶EA＝1∶2，若AD＝2，BC＝5，则EF＝_______
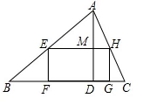
16.如图，矩形EFGH内接于△ABC，AD⊥BC于点D，交EH于M，BC＝8cm，AD＝6cm，EH＝2EF，EH＝_______cm
第11题图 第12题图 第13题图
第15题图
17.如图，正方形ABCD中，AB＝4，E为BC的中点，两个动点M和N分别在边CD和AD上运动且MN＝2，若△ABE与以D，M，N为顶点的三角形相似，则DM＝_______
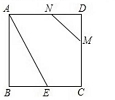
第16题图 第17题图 第18题图
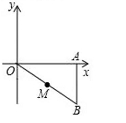
18.假如两个几何图形存在一一对应，且每一对对应点P和P`都与肯定点O共线，同时
＝k（k＞0是常数），那样乘这两个图形位似而点O叫做位似中心，k是位似比，如图，△AOB三个顶点的坐标分别为A（8.0），O（0.0），B（8.－6），点M为OB的中点，以点o为位似中心，把△AOB缩小为原来的，得到的△A`O`B`，以点M`为O`B`的中点，则MM`的长为_______
3、解答卷（本大题共7题，满分78分）
19.（本题10分）已知＝
＝，且2x＋3y＋z＝6，求x＋y－z的值.
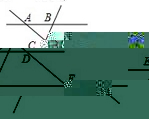
20.（本题10分）如图已知AB∥CD∥EF，AF与BE交于O点，若AF＝9，BO＝2，
OC＝1，CE＝4，求DF和OD的长
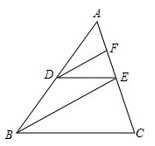
21.（本题10分）如图，在△ABC中，点D在边AB上，点F,E在边AC上，DE∥BC，DF∥BE，求证＝
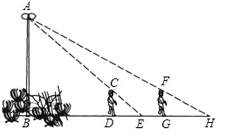
22.（本题10分）如图，花丛中一根灯杆AB上有一盏路灯A，灯光下，小明在D处的影长DE＝3米，沿bd方向走到点G，DG＝5米，这个时候小明的影长GH＝4米，假如小明的身高为1.7米，求路灯A离地面的高度
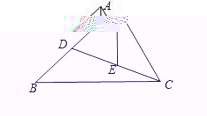
23.（本题12分）如图，在△ABC中，点D在AB边上，点E在线段CD上，且∠ACD＝∠B＝∠BAE
（1）
＝
（2）
＝
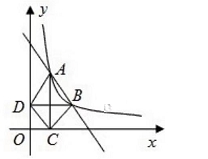
24.（本题12分）如图，在直角坐标平面内，函数y＝
（x＞0，m是常数）的图像经过A,B（a，b）其中a＞1，过点A作x轴垂线，垂足为C，过点B作y轴垂线，垂足为D，联结AD，DC，CB，若△ABD的面积为4，
（1）求点B的坐标
（2）在x周的负半轴上是不是存在点E，使△DOE∽△DOC，假如存在求出点E的坐标，假如没有，请说明理由
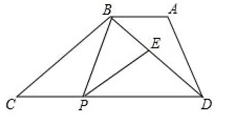
25（本题14分）如图，在梯形ABCD中，AB平层CD，CD＝6，BC＝4，∠ABD＝∠C，P是CD上的东线（P不与点C，点D重合），且满足调价你：∠BPE＝∠C，交BD于点E
（1）求证；△BCP∽△PDE
（2）假如CP＝x，BE＝y,求y与x之间的函数关系式
（3）P点在运动过程中，△BPE能否成为等腰三角形，若能，求x的值，若不可以，说明理由
