3.5 三元一次方程及其解法
1、选择题
1. 解方程组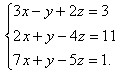 ,若要使运算方便,消元的办法应选取
,若要使运算方便,消元的办法应选取
(A)先消去x. (B)先消去y. (C)先消去z. (D)以上说法都不对.
2. 三元一次方程组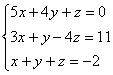 ,消去未知数
,消去未知数![]() 后,得到的二元一次方程组是
后,得到的二元一次方程组是
(A)![]() .(B)
.(B)![]() .(C)
.(C)![]() .(D)
.(D)![]() .
.
3. 三元一次方程组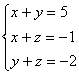 的解是
的解是
(A)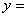 . (B).
. (B).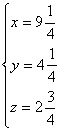 (C)
(C) . (D)
. (D)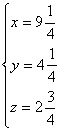 .
.
4. 已知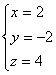 是方程组
是方程组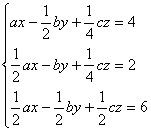 的解,则
的解,则![]() ,
,![]() ,
,![]() 的值为
的值为
(A) . (B)
. (B) . (C)
. (C) . (D)
. (D) .
.
5. 若方程组![]() 的解
的解![]() 和
和![]() 的值互为相反数,则
的值互为相反数,则![]() 的值等于
的值等于
0. 1. 2. 3.
6. 已知方程组![]() 有无穷多组解,则
有无穷多组解,则![]() 的值分别为
的值分别为
![]() .
. ![]() .
. ![]() .
. ![]() 可取任意值.
可取任意值.
7.己知![]() ,
,![]() ,
,![]() 满足方程组
满足方程组![]() ,则
,则![]()
(A)![]() .(B)
.(B)![]() .(C)
.(C)![]() .(D)
.(D)![]() .
.
8. 若三元一次方程组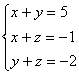 的解使
的解使![]() ,则
,则![]() 的值是
的值是
(A)18.(B)2.(C)0.(D)-2.
10. 若![]() ,
,![]() ,
,![]() 都是不等于零的数,且
都是不等于零的数,且![]() ,则
,则![]()
(A)2.(B)-1.(C)2或-1.(D)没有.
11. 某瓶中装有1分,2分,5分三种硬币,15枚硬币共3角5分,则有多少种装法
(A)1.(B)2.(C)3.(D)4.
12. 学校的篮球数比排球数的2倍少3个,足球数与排球数的比是2:3,三种球共41个,则篮球有多少个?
(A)21.(B)12.(C)8.(D)35.
2、填空题
13.已知![]() 若用含
若用含![]() 的一次式表示,则
的一次式表示,则![]() __________.
__________.
14. 解三元一次方程组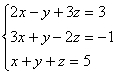 时,若先消去
时,若先消去![]() ,得到关于
,得到关于![]() ,
,![]() 的二元一次方程组是__________;若先消去
的二元一次方程组是__________;若先消去![]() ,得到关于
,得到关于![]() ,
,![]() 的二元一次方程组是__________;若先消去
的二元一次方程组是__________;若先消去![]() ,得到关于
,得到关于![]() ,
,![]() 的二元一次方程组是__________.因此比较简单的办法是先消去__________.
的二元一次方程组是__________.因此比较简单的办法是先消去__________.
15. 已知代数式![]() ,当
,当![]() 时,其值为
时,其值为![]() ;当
;当![]() 时,其值为3;当
时,其值为3;当![]() 时,其值为35. 当x=6时,其值是__________.
时,其值为35. 当x=6时,其值是__________.
16 若![]() ,则
,则![]() __________.
__________.
17 甲、乙、丙三数的和是26,甲数比乙数大1,甲数的两倍与丙数的和比乙数大18,那样甲、乙、丙这三个数分别是_______.
3、解答卷
18解下列方程组.
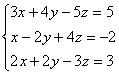 ;
; 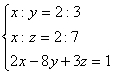 .
.
19.关于![]() ,
,![]() ,
,![]() 的方程组
的方程组 和
和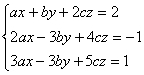 的解相同,求
的解相同,求![]() ,b
,b![]() ,c
,c![]() 的值.
的值.
20 有一个三位数,个位数字是百位数字的3倍,十位数字比百位数字大5,若将此数的个位数与百位数互相对调,所得新数比原数的2倍多35,求原数.
21 假如![]() 与
与![]() 是相同种类项,求
是相同种类项,求![]() ,
,![]() ,
,![]() 的值.
的值.
22.某农场300名职工耕种51公顷土地,计划种植水稻、棉花和蔬菜,已知种植植物每公顷所需的劳动力人数及投入的设施奖金如下表:
农作物品种 | 每公顷需劳动力 | 每公顷需投入奖金 |
水稻 | 4人 | 1万元 |
棉花 | 8人 | 1万元 |
蔬菜 | 5人 | 2万元 |
已知该农场计划在设施投入67万元,应该如何安排这三种作物的种植面积,才能使所有职工都有工作,而且投入的资金正好够用?
23.今有上等谷子三捆,中等谷子二捆,下等谷子一捆,共得谷子三十九斗;假如有上等谷子二捆,中等谷子三捆,下等谷子一捆,共得谷子三十六斗;上等谷子一捆,中等谷子二捆,下等谷子三捆,共得谷子三十三斗.上、中、下三等谷子一捆各多少斗?







