上海2020-2021学年南汇中学高中一年级上学期数学期中考试
1、填空题（本大题满分36分）本大题共有12题，每一个空格填对得3分
1.用列举法写出集合
______________
2.若集合
，则
____________
3.函数
的概念域是_____________
4.命题“若
且
，则
”的否命题是_______________
5.设集合，集合
，若
，则实数
___________
6.已知
，且
，则实数
的取值范围是___________
7.若，则
的最小值是___________
8.不等式的解集为___________
9.若不等式
无解，则实数的取值范围是_____________
10.已知集合
若，则实数
的取值范围是___________
11.设集合
，若
，把
的所有元素的乘积称为的容量（若中只有一个元素，则该元素的数值即为它的容量，规定空集的容量为0）.若的容量为奇（偶）数，则称为的奇（偶）数子集，则的所有奇子集的容量之和为_______
12.研究问题：“已知关于
的不等式
的解集为
，解关于的不等式
”有如下解法：由，令
，则
，所以不等式的解集为，参考上述解法，已知关于的不等式
的解集为
，则关于的不等式的解集为_____________
2、选择题（本大题满分12分）本大题共有4题，每题只有一个正确答案，选对得3分
13.“
”是“
”的（ ）
A.充分非必要条件 B.必要非充分条件 C.充要条件 D.非充分非必要条件
14.下列四组函数
和表示同一函数的是（ ）
A.
B.
C. D.
15.已知下列命题
（1）若
，则
（2）若
，则
（3）若，则
（4）已知，若，则
其中真命题的个数为（ ）
A.0 B.1 C.2 D.3
16.已知集合，对它的非空子集A，可得A中的每一个元素都乘以
再求和（如
，可求得和为
），则对M的所有非空子集，这集和的总和是（ ）
A.25606 B.5120 C.28160 D.2018
3、解答卷（本大题满分52分）本大题共有5题，解答下列各题需要在答卷纸上与题号对应的地区内写出必要的步骤
17.（本题满分8分）
求关于的不等式组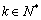
的解集
18.（本题满分8分）
已知，若非空集合，求实数
的值
19.（本题满分10分）
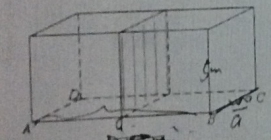
某校第二教学楼在建造过程中，需建一座长方体的净水处置池，该长方体的底面积为
，池的深度为，如图，该处置池有左右两部分组成，中间是一条间隔的墙壁，池的外围墙壁建造单价为
元/㎡，中间的墙壁（不考虑该墙壁的左右两面）建造单价为100元/㎡，池底建造单价为60元/㎡，池壁厚度忽视不计，问净水处置池的长AB为多少米时，可使总造价最低，最底价为多少元？
20.（本题满分12分）
设集合
（1）求出集合
（2）若
且
，求实数的取值范围；
（3）若
且
求实数的取值范围
21.（本题满分14分）
对在直角坐标系的第一象限内的任意两点作如下概念：，那样称点
是点
的“上位点”，同时点是点的“下位点”
（1）试写出点
的一个“上位点”坐标和一个“下位点”坐标；
（2）设均为正数，且点是点的上位点，请判断点是不是既是点的“下位点”又是点的“上位点”若是请证明，假如不是请说明理由；
（3）设正整数
满足以下条件：对任意实数
，总存在，使得点既是点的“下位点”，又是点
的“上位点”，求正整数的最小值.
