第7课时平面向量应用举例
基础达标
1.在△ABC中,已知点A,B,C,则BC边的中线AD的长是.
A.2
B.
C.3D.
【分析】由题可知,BC边的中点为D
,
=
,
所以||=.
【答案】B
2.已知点P在平面上做匀速直线运动,速度向量v=.设开始时点P的坐标为,则5 s后点P的坐标为.
A. B.
C. D.
【分析】设5 s后点P运动到点A,
则
=
-
=5v=,
∴=+=.
【答案】C
3.若四边形ABCD满足
+
=0,·
=0,则该四边形肯定是.
A.正方形 B.矩形 C.菱形 D.直角梯形
【分析】∵
+
=0,∴=,∴四边形ABCD是平行四边形.由·
=0,得
·=0,∴⊥,即此平行四边形对角线互相垂直,故肯定是菱形.
【答案】C
4.甲、乙两人同时拉动一个有绳相缚的物体,当甲、乙所拉着的绳子与铅垂线分别成30°、60°的角时,甲和乙的手上所承受的力之比是.
A.1∶B.∶1C.1∶
D.∶1
【分析】设物体重量为G,则|F甲|=Gsin 60°=G,|F乙|=Gsin 30°=G,
∴|F甲|∶|F乙|=∶1.故选D.
【答案】D
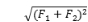
5.如图,用途于同一点O的三个力F1,F2,F3处于平衡状况,已知|F1|=1,|F2|=2,F1与F2的夹角为
,则F3的大小为__________.
【分析】∵F1,F2,F3三个力处于平衡状况,
∴F1+F2+F3=0,即F3=-,
∴|F3|=|F1+F2|=
=
=
=.
【答案】
6.已知△ABC的外接圆的圆心为O,半径为1,
=
,且||=||,则
·
=__________.
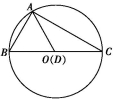
【分析】设BC的中点是D,如图所示,则+=2,故=
,∴点O和点D重合,
∴BC是圆O的直径,
∴∠BAC=90°.
又||=||,∴|
|=1,
∵|
|=2,∴∠ABC=60°,
∴·=||||cosplay 60°=1×2×=1.
【答案】1
7.某物体遭到两个大小均为60 N的力有哪些用途,两个力的夹角为60°,且有一个力的方向为水平方向,求合力的大小及方向.
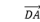
【分析】如图,设,
分别表示两个力,以OA,OB为邻边作▱OACB,则
就是合力.依据题意,△OAC为等腰三角形且∠COA=30°,过点A作AD⊥OC,垂足为D.在Rt△OAD中,||=||·cosplay 30°=60×=30,故||=2||=60.故合力的大小为60 N,方向与水平方向成30°角.
拓展提高
8.已知点O,N,P在△ABC所在平面内,且||=||=|
|,
+
+
=0,·
=·
=·,则点O,N,P依次是△ABC的.
A.重心,外心,垂心 B.重心,外心,内心
C.外心,重心,垂心 D.外心,重心,内心
【分析】||=||=||,则点O是△ABC外接圆的圆心,点O为外心;
+
+
=0,则点N为△ABC的重点;·=·
,则·=0,即·
=0,即PB⊥CA,同理PA⊥BC,PC⊥AB,故P为△ABC的垂心.
【答案】C
9.已知||=1,||=,·=0,点C在线段AB上,且∠AOC=30°,设=m+n,则等于.
A.
B.3 C. D.
【分析】∵||=1,||=,·=0,∠AOC=30°,
∴△AOC为直角三角形,其中AC=
AB=.
∴=+=+
=+=+.
∴m=
,n=,即
=3,故选B.
【答案】B
10.在长江南岸渡口处,江水以12.5 km/h的速度向东流,渡船的速度为25 km/h.渡船要垂直地渡过长江,则船行驶的方向为__________.
【分析】如图所示,渡船速度为,水流速度为,
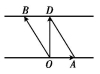
则船实质垂直过江的速度为.
依题意知||=,||=25,
由于=+,所以·=·+.
由于⊥,所以·=0,
所以25×cosplay+=0,
化简得cosplay=-,即sin∠BOD=,
所以∠BOD=30°,故船行驶的方向为北偏西30°.
【答案】北偏西30°
11.在四边形ABCD中,=,=,=.
若∥,试求x与y满足的关系式;
满足的同时又有⊥,求x,y的值及四边形ABCD的面积.
【分析】=, =-=-=-=.
若∥,则有x-y=0,化简得x+2y=0.
=+=,
=+=.
∵⊥,∴+=0,
化简得x2+y2+4x-2y-15=0,
由
解得或
∵∥,⊥,
∴四边形ABCD为对角线互相垂直的梯形,
当时,=,=,此时S梯形ABCD=||||=16;
当
时,=,=,此时S梯形ABCD=||||=16,
故四边形ABCD的面积为16.
