「2021年上海蒙山中学上教版初三物理上册训练」7.2 欧姆定律 电阻

§7.2欧姆定律 电阻（三）

1、选择题

1．温度肯定时,比较两根铜制导线电阻的大小,下列正确的是

A. 长导线的电阻的肯定大              B. 细导线的电阻肯定大

C. 粗细相同,长导线电阻肯定大         D. 粗细相同,短导线电阻肯定大

2．导体的电阻 [来源:Zxxk.Com]

A. 跟导体两端的电压成正比            B. 与导体中的电流强度成反比

C. 决定于电路中的电流强度和电压      D. 决定于导体的材料、长度和横截面积

3．一个导体两端的电压由小变大，可以判定导体的电阻值
A. 增大         B. 维持不变       C. 减小

4．用滑动变阻器时，闭合开关前，应把滑动变阻器的滑片调到阻值最大，下列图1中滑片地方正确的是：   （   ）[来源:学base64,/9j/4AAQSkZJRgABAQEAYABgAAD/2wBDAAEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQH/2wBDAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQEBAQH/wAARCABXAdEDASIAAhEBAxEB/8QAHwAAAQUBAQEBAQEAAAAAAAAAAAECAwQFBgcICQoL/8QAtRAAAgEDAwIEAwUFBAQAAAF9AQIDAAQRBRIhMUEGE1FhByJxFDKBkaEII0KxwRVS0fAkM2JyggkKFhcYGRolJicoKSo0NTY3ODk6Q0RFRkdISUpTVFVWV1hZWmNkZWZnaGlqc3R1dnd4eXqDhIWGh4iJipKTlJWWl5iZmqKjpKWmp6ipqrKztLW2t7i5usLDxMXGx8jJytLT1NXW19jZ2uHi4+Tl5ufo6erx8vP09fb3+Pn6/8QAHwEAAwEBAQEBAQEBAQAAAAAAAAECAwQFBgcICQoL/8QAtREAAgECBAQDBAcFBAQAAQJ3AAECAxEEBSExBhJBUQdhcRMiMoEIFEKRobHBCSMzUvAVYnLRChYkNOEl8RcYGRomJygpKjU2Nzg5OkNERUZHSElKU1RVVldYWVpjZGVmZ2hpanN0dXZ3eHl6goOEhYaHiImKkpOUlZaXmJmaoqOkpaanqKmqsrO0tba3uLm6wsPExcbHyMnK0tPU1dbX2Nna4uPk5ebn6Onq8vP09fb3+Pn6/9oADAMBA人工智能RAxEAPwD+vn9vTxH8U/gl4c8I/tVfCHx/jxb8Ls/CLT/2b/Ftn4j1b4WftW+I/wBpf4p/BLwR8LfhAkmheNfBGmfCH9oDx58bdC+GHwX+CP7WHxAHxD+Fn7Nvhz40/GXX/iR8JPF/hLxJqeseEvv+vkD9uj4W+O/i3+z/AA6N8NtC/wCEr8W+BP2gP2O/2hLbwdBqej6PrHjjR/2V/wBr/wCBf7TPizwH4R1HxNqGieErf4geOPCXwk1zwn8Ol8beJvBvgS48d6x4dtvHPjvwJ4Sm1nxhohZ/t+fsbf8ACifDn7S/i79oT4f/AAX+CXiv4geNfhPo/jX9pe8vv2V/+Lp/Dnxj4/8AAHjf4aat4c/aQsPhZ4t8OfEDw54t+FnxF0m/8G+ItB0rxH/xRuvX8GmzaZYyXtAH1/RRRQAUUUUAFFFFABRRRQAV8gftw/FLx38H/gv4K8WfDrXf+Ed8Qav+1/8A8E9vhbqGof2Zo+r/AGjwJ8cf2+v2afgp8UtC+y67p+p2UX/CUfDL4geLvDP9pwW0WsaJ/a/9s+HdQ0jxBYaZqtl6/wDGv9oX4Bfs1+FdP8dftGfHH4P/AAB8E6t4gtfCel+MfjX8S/Bfwr8K6l4qvtO1XWLHwzp/iHx1rWg6ReeILzSNC1zVLXRre8k1G407RtVvobZ7bTryWH4g8ceNf+HiOsfBzwt+zfe/D/4hfsV+Cf2gPgt8Z/jd+1bonj/7To/xB8R/s3eO9K/aI+E3wz/Y0v8Aw54c8ZeDPjb/AGL+0b8Kvg/pH7UvxQ1DW9E+FnhDwJc/EH4F/C7xR42/aV074q2/7LYB+n9FFFABX5gfs7ftL/8ACnv2p/iP/wAE8v2kNW+IFh8WvGPxA+Pn7RX7HXxb+KF/9q8Hftf/AAJ+JXxF8TfHXxP8OPgx4guNe8Q/2f8AED9hX/hY0n7Pvij4B6xqtr4xtfgT8Nfhn8fvBHhmw+EvjG88NfCz9P6/OD/gqPo2o+Gv2av+Gv8Aw14s8QeGvG3/AATa8QeJv+CgHhXR9GtvCtzp3xY074J/BD4xeHvi78AvFkvirwz4pj0Hw/8AHz9nz4h/F/4R23j/AECwHir4T+KvF/hn4s6FbeIbnwOfB3iUA/R+ivH/人工智能KftC/AL9pTwrqHjr9nP44/B/4/eCdJ8QXXhPVPGPwU+Jfgv4qeFdN8VWOnaVrF94Z1DxD4F1rXtIs/EFnpGu6Hql1o1xeR6jb6drOlX01sltqNnLN7BQAUUUUAFFFFABRRRQAUUV4/8FP2hfgF+0p4V1Dx1+zn8cfg/wDH7wTpPiC68J6p4x+CnxL8F/FTwrpviqx07StYvvDOoeIfAuta9pFn4gs9I13Q9UutGuLyPUbfTtZ0q+mtkttRs5ZgD2CiiigArz/4s/8AC0/+FWfEv/hRf/Cv/wDhdv8Awr/xl/wp3/hbP/CR/wDCrP8Ahaf/AAjmpf8ACvv+Fl/8If8A8Vb/AMK//wCEt/sj/hMv+EW/4qP/人工智能Rz+0v7E/4mf2WvQKKAPAP2b/2l/hZ+1N4E1jxr8MdW3Xvgn4geN/g18XvAGp3/人工智能cufHfwP+O3wt1iTw58VPgj8UrPwpr3ijw/pnxA+H/iCJrLUH8P+I/Eng7xRo9zoXj/AOHHi3xt8MvF/gzxr4h9/r8wPjJ4K/4Z7/4KHfsnfHX4O2Xw/wDCf/De/wAQPEf7Jv7aGj/8IB5/iP41/wDCnf2Sv2lv2kP2Xfi9/wAJvY+I9K/sD4gfAb/hSHxB+En2i68NeIv+Fk/Cz43f8I/4wu3/AOFJ/BOTwd+n9ABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRXzB+0z8FvjL8UtO8HeIf2d/2k/EH7M3xk8AeINOvdJ8R3Xg+D4y/Brx14Lu/FXg/W/iD8L/jX8ANa8T+ENI8beH/ABtpHhC20fSvH3gvxj8LPj78K57jUJfhV8ZPCXhvxd8U/CHxI点对点P2mdO/ay+AXgT4tS+DvEHwm+Il54f8L2vxw+AHjnTvFWhfEz9nL4y6h4L8MeL/FvwU+JPhzx34P+HnjbS/EHhi28VaPqWh6r4h8B+FIPiN8Pde8E/Fzwdp958O/iD4P1vVQD6fooooAKKKKACiiigAooooAKKKKACiiigAooooAK/GH9pn9kP4reAf8AgoX4O/4KLfA6y/af8cW138H9O+Dfj74Afsi69+xf4R1HxH4gHj7wf4v8fePvix4c/bUi8P8Aw7+IHh/4/wDw7+D/AMAvgj8S/ih8MPjF8E/2oPht4V/Zm+Bngrwne/FLwT4l/tv9mP8AZ6viD9o74s/H1fj78C/2XP2c/Efwf+G3jb4r/B/9oz4+ap8VvjX8KvGnx28K6X4V/Z08afsx/Dy++Hun/CvwL8bv2cdXfxB441f9qbQ/Elr8Qbj4sSad4T074bar4cm+Hnim58f2fiTwEAfMH7Ln/BOX9qL4L/AnwN8ONd/4Ki/tf+EL3Qv+Emu4PAHwn8Gf8E7dZ+Fnws0fxJ4x8Q+KfDvwf+GmqfEX/gnHceIL34f/AAf8P63pnwx8Gzaf4f8Ahd4E/wCEc8J6avwt+Av7OvwyXwj8CPh1z/wC+EP7WnxU+K37bvgXxD/wVS/bfs9I/Zr/AGn/AAn8FPAtxo3wu/4Jh2+o6t4V179i/wDZE/aMvNQ8WTX3/BOjUba+8QR+Nvj94x0u2utHs9B05PCum+GbGXSptXs9U1zWf1e+E/8AwtP/人工智能VZ8NP+F6f8K/8A+F2/8K/8G/8AC4v+FT/8JH/wqz/haf8Awjmm/wDCwf8AhWn/AAmH/FW/8K//AOEt/tf/人工智能Q3/hKf+Kj/AOEc/s3+2/8AiZ/aq+QP2N/+Tiv+CsX/AGf/APDj/wBdZf8ABNOgA/4Y3/aK/wCksX7f/wD4bn/gll/9LTo/4Y3/AGiv+ksX7f8A/wCG5/4JZf8A0tOvv+igD4A/4Y3/AGiv+ksX7f8A/wCG5/4JZf8A0tOj/hjf9or/AKSxft//APhuf+CWX/0tOvv+igD4A/4Y3/aK/wCksX7f/wD4bn/gll/9LTo/4Y3/AGiv+ksX7f8A/wCG5/4JZf8A0tOvv+igD8IfjX+wv+0j4I+Pun/HXxL8ev8Ago//AMFCfht4g+D9r8FNU+FPwm+KP7C37LHx9+H09n401X4h32oeHPip4F8I/sB6v4Y+D/xO1e38Aan8Vbr9nH9o/wDZ5+MuueNPgL8EfCPxq0r9sL4E67Z+G/2XP0//AGNvgp4q/Z6/Z48HfCrxjqHh+XV9J8QfFPxJZ+F/Bl1qN/8AD34QeFfiP8W/HXxK8C/s5fCu/wBU0rw3c3/wf/Zi8E+LvD37O/whv4vBfw4069+Gfww8KXOj/Cr4U6RLY/Dnwv8AL/gD9vn4p6j+1341/Z0+KX7Pnw/8HfD+w/a/8R/sU/Dr4peAP2gfEfxK8Y+Kvina/sUWf/BQ7wjr/jX4UeIv2efhRovgH4f65+zK+oWPiPVdC+LvxK8R+Ffjta2fw70zwp4x+H9/P8Z9O/T+gAooooAK+IP+CkP7K3ir9tz9iX4+fsseDviL4g+GGr/GDw/4e0S817wz4u1H4f6j4h8K6T448L+KPHXwnufHul+HfG1z4G8P/HTwToXiH4KeLPGUvw7+K2neFvCvxA1nXdY+D3xg0iwvvhl4r+368f8A2hfjX4V/Zr+AXxw/aM8daf4g1bwT8Afg/wDEv41+MdL8J2unX3irUvCvwr8F61468Q6f4ZsdY1XQdIvPEF5pGhXlvo1rqmuaNp1xqMltDfarp1s8t5CAfnD/AMM9/tRftV/tT/8ADVkHjz9r/wD4JeeH/D37P/8Awz3qfwx01v8Agnb49+Kfx31iP4i/8LH0Lx54yXT/AAJ+2z8MrL4f/Cqy1LxF4f8Aho3i74m+PPHZ8R/Ev4sj4deBP2V/D8nxS8Qftue//wDDG/7RX/SWL9v/AP8ADc/8Esv/AKWnXsHwD8eftceJ/FXxC8PftOfs3/B/4MaRoHh/4faz8PPHXwU/af1v9orwr8Q9R8S6j8Q7Hxx4T1Cz8Z/s6fs0+NvBHiD4bW3hbwTrF1c3fg7W/CvirTvifpUXh3xNNq/hjxbpel/T9AHwB/wxv+0V/wBJYv2//wDw3P8AwSy/+lp0f8Mb/tFf9JYv2/8A/wANz/wSy/8Apadff9FAH4w+LPhD+1poX7aHwC/Zzs/+CqX7b8ngn4qfswftd/GvxDqlz8Lv+CYb+KrPxV8Afit+xF4F8Hafo19F/wAE6IdIt/D+paR+0p46uPE1rfaHqOo3mo6T4Tm0vVdGtrHWLPXvp/8A4Y3/AGiv+ksX7f8A/wCG5/4JZf8A0tOj4jf8pTf2N/8AswD/人工智能KWf+tFf8Ena+/6APgD/hjf9or/AKSxft//APhuf+CWX/0tOj/hjf8AaK/6Sxft/wD/人工智能bn/gll/wDS06+/6KAPyB/aj/4Jy/tRfGj4E+OfhxoX/BUX9r/xfe67/w人工智能zdz+APiz4M/4J26N8LPino/hvxj4e8U+Ivg/8S9U+HX/AATjt/EFl8P/人工智能weH9E1P4Y+MptQ8P8AxR8Cf8I54s1Jfil8Bf2ivhk3i74EfEX1/wDZx8DfG/x38ffCH7RnxG+G3xg+ANt8Of2YNX/Zi8W6X8fdc/Zq1X4+/tceKr7xp8NfHXhb40fGGx/Y18beMv2fNF8P/AuPwv8AEq3+DsFhrkmoz+NP2sv2o4fDHwf/AGcvBOnWF5+0J+j9fkD4A/bE/an079t3xr8Gfilqf7P/人工智能x+CV/+3/4j/YY+HWk+APg/8Rfhr8U/Cv2r/gmpZ/8ABTjwj8UfGvxF8RftB/Ffwl4+/sPwkmofs9eI/BOhfCT4a/8ACVeI7qz+OGmeLvB2mWE/wT1EA/X6iiigAooooA/nh/4KBfs0z/E79pGfxl8ePAPxg+KXjfwj8YJPiL/wTs1v4Zfs0/GX9o/wrovhW/8A2FvGfwAsvgKfF/wd8ffBGw/Yj+MHhf8Abw+I4/bG8QftK/En40/svad4107w7+ym+k/to6Jc/syW3iP9hj2D4s67/wAFiP2SP2BfiX+0F8Uv2s/2APin8Tf2ZP2QPGXxj+Iuh/8ADBfxyb/hY3jv4L/BfUvG3i7Sv+Fk+Hf2+fhb4fb/人工智能S/xB4b1Cz/AOE40L9nb4daOf7R/t7TPgt4RsvI8Daf9/8A7S/7d37M/wCyN/a3/C7fFHxAtf8AhGPh/f8AxY8ef8Kv+AH7Qn7Qn/CqvhZYf29t+Jfxn/4Z7+FnxR/4Ut8P9W/4RDxz/w人工智能v4y+K/8Awh3hzxf/AMK6+Jn/AAiupaz/AMK18d/8I95//wAFYv8AlFl/wUs/7MA/bI/9Z1+I1AB/wrn/人工智能Km/wDR5H7AH/itP9or/wCmxUf8K5/4Km/9HkfsAf8AitP9or/6bFX3/RQB8Af8K5/4Km/9HkfsAf8AitP9or/6bFR/wrn/人工智能Km/wDR5H7AH/itP9or/wCmxV9/0UAfAH/Cuf8Agqb/ANHkfsAf+K0/2iv/AKbFR/wrn/gqb/0eR+wB/wCK0/2iv/psVff9FAHwB/wrn/gqb/0eR+wB/wCK0/2iv/psVfnB45+C3xbsv2oPiTrv/BT74feH/wBvK28R+H9DtP2CdR/ZN/4J9ftDweKvhZ4qh8P+CbKfTPgj8fNP/aj+LXhb/gmx8YLH4rWnibxL4j+NvxV1/wCBuo+LdR8afAD4v2P/AAUdtfBP7Nc/wP8A2M/6Hq+AP22Pih+1P4E+Iv7E3gD9mjx5+z/4E/4aV/aA8ffAvxrq3x0+AnxF+Of9j/2N+yx8f/2l/DfinwtYeAP2mv2cfsv2X/hnHXvBWt6Jq15rH9sf8LC0jxHYavoH/CCXmg+OwD6f/Z60b4y+HPgF8D/D37Rnizw/49/aD0H4P/DTRvjt468J20Fn4V8afGXS/Bei2PxP8WeGbO18M+C7a18P+I/G0Guaxo1tb+DvCcEGnXltFD4Z0KNV0u19grwD9k746f8ADUH7LH7NP7S//CLf8IP/AMNEfs//AAb+On/CFf23/wAJN/wh/wDwtv4deHPH/wDwi3/CR/2R4f8A+Eg/4R//人工智能SD+yf7b/sHRP7V+yfb/wCyNN+0fY4ff6ACiiigAr8Qf+CgX7O/gTxL+1P4d+Nf7S/wd/4XN+zlJ8P/ANnzwt4X8PaR+wprH/BQPw5e+O/hr8Rf2j9T+M/gv9oj9nz4Z/DDx78YLz/hOfg/8atB1D9jT9ofSdK13R/2Ufin4D+OVrf+K/h54M/aU+KH7PP7fn7fV8wftO/HzxV8FYPgv4V+Gvw98P8AxM+Mn7Rnxgn+Cnwg8M+OfiDqPwn+GZ8VaP8ABr4wftC+JdQ+JPxL0D4efGHxT4P8P2nwp+A3xGGh3Xhf4RfEXUdZ+IU3gnwrf6V4e8N6/rvj7weAfEH7Lnwc/wCCxHhv4E+BtG+Iv7XH7IGieILX/hJpNP8ADfxZ/Yl+OXxr+KfhDwJe+MfEN/8AC3wR8S/iroX/AAVPtrLxt8QPBPwyufCPhPxlrE/ib4waw3iPRtStvEX7SH7UXiC31P8AaN+KPv8A/wAK5/4Km/8AR5H7AH/itP8AaK/+mxV9P/AjxX8ZfGnwz0vXvj/8IfD/AMC/isfEHj/RvEPw58J/FSD41eFbXTvC/wAQvFPhfwd4s8M/EqLwZ8OrnX/D/wATPBOj+HPibo1trfgLwb4q8Oad4wtvC/i/wzo3inRdYsIPYKAPgD/hXP8AwVN/6PI/YA/8Vp/tFf8A02Kj/hXP/BU3/o8j9gD/AMVp/tFf/TYq+/6KAPgD/hXP/BU3/o8j9gD/AMVp/tFf/TYqP+Fc/wDBU3/o8j9gD/xWn+0V/wDTYq+/6KAPgD/hXP8AwVN/6PI/YA/8Vp/tFf8A02KvAP2afFv/AAVN/aI+HXiPx/8A8NQfsAeD/wDhH/2gP2sfgX/ZP/Du79orxB9r/wCGX/2p/jJ+zR/wlP2//h6Xon2f/hOP+FSf8Jr/AGJ9jm/4Rn/hIP8AhHP7X8Qf2V/b2pfr9XwB/wAE0/8Ak3X4jf8AZ/8A/wAFYv8A16b+2RQB8waz+xT+1x8ff2uPCcf/AAUG1b9iD9s39i/RPg/c6hoXw1uP2Jdb0z4e+GPjLY634msNf1Wb4c/F/wDbc+M+kaJ8YPEukeJ/hpcfD341618O/wBpWCx+Gfw/+P3wo8JWv7HGo/EbxL4o/a3+/wD9jbwz8ZfCH7PHg7Qfjtc+IH8bW/iD4p3uh6T4z8WQeP8A4heCfg1rPxb8da1+zn8L/ip8QbfWfFcfxB+MHwm/Z81D4YfDL4vePm8e/FSfxt8TPCXivxRdfGT4y3OrTfFPxf5//wAFL/HPxM+Ff/BPT9tj4u/Bn4k+IPhH8Vvgx+zB8avjX8PvHvhnQ/h74l1HSfFXwc8A658TdJ0+50H4p+CfiH4J1Tw/4nufCqeFfFlrqPhW51F/Cut6yfDGq+GPFK6L4o0Y/Yw8c/EzVNb/AGwPgv8AE34k+IPjLc/sqftP6N8FPCvxa8c6H8PdA+Jnj3wr4t/ZH/ZU/afOofEm0+EXgn4YfCmfxBoHin9orxR4J0O68BfC7wBpzfD3wt4Jg17Stc8bW/irxz4sAPt+iiigAooooAK8A+On7MXwi/aK/wCEWufiLafEDTPEHgr+24PC3j34O/Gz42fs5fFPRtH8Uf2RJ4r8I2vxb/Z4+IXwt+JrfD/xfe+G/COs+MPh1P4sl8CeLPEfgX4feJvEXh3U/EHw/wDBepaF7/RQBz/hPwn4V8BeFfDPgXwL4Z8P+C/BPgvw/o3hPwd4O8J6Np3hzwr4T8K+HNOttH8PeGfDPh7R7az0jQfD+haRZ2el6No2l2drp2l6da21jY20FtBFEvxB+xv/AMnFf8FYv+z/AP4cf+usv+CaddB/wUo+Nfx9/Zr/AGDP2qv2jP2Y9P8Ag/q3xk+APwf8S/GvRdL+O9r40vvhnqXhX4VpD46+Ken6pY/D7VdB8U3niC8+FOheNrfwBa2muaNp1x8QpPC0PiLVdO8Nvq15D+APwP8A+Ch3xM/ar/bvvfgP/wAE7vFXiDwF8RP2iv23/wBjH/gqB+05Y/Enwd8PYNO8Lf8ABJbVP+CVf/BNez8beEPG2qeIrTx/bW/xg+Mvjbxb4Q+G3gbQPgIfFni7QPFWga5q3if4gfDD4dtaeOtcAP63aKKKACiiigAooooA+APAH/BPfwd4O/aY8a/tNeIvjx+0B8V9T8VftAeI/wBqPQvhV4/f4E6d8LPhr8dtc/Z7s/2RdM8c+Cm+FvwK+GvxSv8A/hDv2UrWf4CeHPDPxF+KHj7wddeHNRvfHni7w94q+Nqaf8U7D7/oooAKKKKACvP/人工智能s/C3wJ8cfhZ8S/gp8UtC/4Sj4ZfGD4f+Mvhb8RfDP9p6xon/CReBPiB4c1Lwn4u0L+2fDuoaR4g0j+1/D+r6hp/wDaeharpmsWH2j7VpmoWV7FBcxegUUAeAfAv4HeI/hD/wAJTqHjX9o39oD9pfxb4q/sSzl8XfHTUvhZp39heHPDf9rz6L4c8LfDr9n/AOFHwI+CWg+XqfiPxHqet+NbP4Wj4p+N/wC0dI0Lx/4/8VeEvh58KfDvgP3+iigAoorn/Fnizwr4C8K+JvHXjrxN4f8ABfgnwX4f1nxZ4x8Y+LNZ07w54V8J+FfDmnXOseIfE3ibxDrFzZ6RoPh/QtIs7zVNZ1nVLy107S9Otbm+vrmC2gllUA+IPiN/ylN/Y3/7MA/4KWf+tFf8Ena+/wCvzg1rxZ4V8e/8FJP2EfHXgXxN4f8AGngnxp/wTg/4KJ+LPB3jHwnrOneI/Cvizwr4j+PP/BJTWPD3ibwz4h0e5vNI17w/rukXlnqmjazpd5dadqmnXVtfWNzPbTxSt9QfsuftR/An9tH4E+Bv2l/2aPHP/Cyvgl8Sv+Em/wCEK8a/8Iz4x8Hf21/wh3jHxD4A8R/8U54/8PeFfFunf2d4t8K69pP/ABNtBsPtn2D7fYfatMurK9uAD3+iiigAr5A8AfsI/sz/AA1+O3jX9pLw74X+IGo/Frx98QPEfxY13UvH/wAf/wBoT4r+DrD4p+KvB1n8NNT+Jfgr4T/FL4p+MfhL8NfiBa/CWwg+Cfhzxl8OvA/hXxH4O+BL3vwO8I6lofwl1HUPBt19f0UAFFFFABRRRQB8AfFD4O/tT+GP2p/Hn7QH7NFr+z/4h/4X3+z/APAT9nrxre/HTxh8RfDH/ChP+GffiL+01418OfFvwt4A8AfD3xZ/w07/AG9/w1Zr0ut/BnVvit+yb5X/AAqfSNFsPjfF/wALVvfEfwnP+CsX/KLL/gpZ/wBmAftkf+s6/Eavv+v5wf2w/wBtb4p638E/+C7f/BPv9rbQPh/4Q+PXgn9gD9uH9qP9k+f4SaV4jufAnxg/4Jx+JPhF40+HXw78c+JfEWseK/FF7pn7QHw/+JsWu/D746+GfEOifC7S73WLnw/rnwc8PeNvAq6t4utwD+j6ivzA+Hf7a3xT+K//AAVw/aL/AGJ/AGgfD/X/ANmX9k39kD4ReMv2gPH/APZXiPS/in4B/bJ+O/je+8SfCn4T/bNa8V6dovir4f8Air9mXTrz4jf2l4K+HfiOx0PxHD/Y/iP4l6PrUkXgp/0/oAKKKKACiiigAr5g/aN/Y9+CH7Veo/CrWPi+vxgXV/gl4g8SeLPhfqnwk/aY/aV/Zy1Hwt4q8WeFb/wLrXiaO+/Z2+LfwrudW8QP4J1nxL4O03Wddl1TUdA8K+MvHvh7QLnTNI8e+MrPXPp+igDn/CfhPwr4C8K+GfAvgXwz4f8ABfgnwX4f0bwn4O8HeE9G07w54V8J+FfDmnW2j+HvDPhnw9o9tZ6RoPh/QtIs7PS9G0bS7O107S9OtbaxsbaC2giiXoKKKACiiigArwD9oT9nvR/2gNH8Bq3jz4gfCT4gfCT4gL8Uvg98Yfha3gS48d/C/wAd3HgTx38J9b13QtE+LHgT4p/CXxH/AMJH8Jfin8TvhxqemfEf4Y+ONHtNH8cah4g8P6fonxA0Twb4y8M+/wBFAHn/AMLfAH/CsPAmheCpPGvxA+JF7pn9p3ms+P8A4peI/wDhKPHfjLxH4g1jUPEfibxHrt5bWWkeH9I/tfxBq+pXumeCvAfhzwZ8LPh3o8un+APhJ4A+H/wy8NeE/BWg+gUUUAFFFFABRRRQAV8Af8E0/wDk3X4jf9n/AP8AwVi/9em/tkVz/wDwUA/ap+Pv7GGo/AL4/wCl/Drw/wCOf2D/AAn4g8fw/wDBRLxD4f8ACPjTx7+0P8EfhnqHhW2i+GHx++GXg7wz4i0m21n4P/Cvxul9rf7VlxZ+HPiX8QvDXwkceL/Avw91Sw8PeMtY0H8gf2Yv20PiZ+0Hq3wB/ZX/AOCYXxf8P+NPEmgf8FX/ANt/9qn9vb4qeDrL4e/EX4BeA/8AgnV4j/4KXfty+JIPh14w+K2oaP430jSvjB+2LpGpeGdZ/Zm8I/Cq2uvih4i8F6PqPxXvvEXwz+Dc8HxD1cA/pd+KXwn+Fnxx8Ca78LfjX8NPh/8AGD4ZeKP7M/4Sb4dfFLwb4c+IHgTxF/Ymsaf4i0b+3fCPizTdX8P6v/ZHiDSNK13TP7Q0+4+waxpmn6na+Ve2VtPEfC34T/Cz4HeBNC+FvwU+Gnw/+D/wy8L/ANp/8Iz8Ovhb4N8OfD/wJ4d/tvWNQ8Raz/YXhHwnpukeH9I/tfxBq+q67qf9n6fb/b9Y1PUNTuvNvb25nl9AooAKKKKACiiigAr8QfjZ+1h8dvBXwi/ad/bnX4u/EDw/e/ssftAfEL9nrwt/wTf8J/CTwd4/0f4z+I/DXxstPgl8CPhv8TrjS/hB4t/a6sf2gP2+YfGvwx+KP7Ofjz4ceLvhv8LPhX4E/aT/AGVPG3iD4EftC/DLwZ4/8Y/tRft9XzBceDP2R/HP7XE3iHUfhX8H/Ev7aHwB+D/w98TWfxR1n4Q6JffGX4afBr42a38fvBPgW28J/GjVPCjavpfh/wAWav4C/aD0e58J+FPGJn0+CTxNL4i0bTtO8cWM/iEA+f8AxZ+30nxD8K+JvA/7Jfwe/af179pbxT4f1nRvglb/ALQv/BP79vP4B/ALS/iFeadcx6B4s+OHxX+NnwO+Cfgnw18H/A9yR4z+JdtYfEOz+JnifwXoOteEvgj4Z+Ifxp174f8Aw78VfAH/AATT/ZP/AGR/+CEMH/BQT4GXGreINI+Hej+H7T9vvRfj/wDErR9E8TfEzx3+yP4D+DXh7wh8U/C+r+I/h98O/BviT4q+IP2TfjJ4F+K3jXxf8Pvh38PvEWifCb4e/tafs430eo33xE/aD1bRE/oer5g/aG/ZD+DX7Tvir9nzxf8AFGy8QPq/7N/xg8PfGTwdL4W16fwnP4k1HwnqOmeMfD3gHx/rGjxQeJPEfwftfjJ4L+C/x/1T4Xwa3pfhXxd8Zf2dvgR4j8bWXiTSPAUXh6/APj/9kPxZ+0/8IfjLZeEf2z/E3iC81f8Ab28P69+0r8OfD3ijWfD+uad+y38fdBgil+JX/BOXw94x8L3Ok/C7WfD/AMK/2bk+D2p/ANPhtpeveNP2kfFX7P3/AAUh/a48eP4c0i8sNHsDxN+158ZbP9ri28eaZe+H5P8Agnf4H+MHhP8A4J/+OryLQYD4g139rj4ya3o2l2fx90Hx1Yy+K5PiD8H/人工智能TftB6h8Cv+Ccdl4A+HWn6HrehftQfGz9r3xB+0Nc+GvCH7Hml3159wftIfAv8A4Xx4E0fStG8U/wDCu/ib8O/iB4I+MXwU+KUOif29dfDz4p/DvWI9T0q6u9PtdX8L+INT+H/xA8Py+Jvgt8evB/hPxx8O/EfxW/Zx+J/xg+Dlt8QvBtl8RNQ12z5/wz+yH8GtG/ZHuf2K/ENl4g+Ivwb8R/B/xZ8G/ijeeM9eng+IXxq074maJrOl/Gjx98VPHXgmLwbq+tfGD46av4o8Y+Pvi98UNH/sDxV4w+JnjTxX4+lvbXxJrE98ADx/9ufU/HfxO/4Vd+w98HPil8QPgl8Tf2r/APhNtT8afGv4T6ho+i/FP4FfsnfBj/hEbr9of4pfDTVfFOhan4fi+IHijxB8QPgt+yv4N1DSryH4k/C3xH+1Dpv7S/gfQvFFl8APFenw+P3v7Xnxl+Iv7Evwvs/DN74f8Eftx/tC/GDx9/wT/wBG13wZoMF78PfA37XHwe8cfGT4QftX/H34V6B8R5fEmkeLPg/+ztpH7N/7Tf7XXwh8AfGXWfDOt/Hj4Z/CDwp8HteufC/xc+KGm+GovYP2GPgX8dvA/wDwtH4x/ta+Kf8AhPf2mvH3/CE/AvUvGv8AYng7wt/bfwJ/ZM/4S7wB8J/FP/COfDTV7v4f6b/w0R8QPE3x5/bq/sSDS7Pxj8JP+Gw/+GY/Eur+JNF/Z98G3tv6B4N/Y68CeDP2yfix+2HY3nm+IPiZ8P8ATfDtp4Z+z6wn/CNeO/EVj8NPCfx6+Iv9szeJ7qy1n/hdfwy/Zd/YW8B/8IjL4YsNH+G//DKv/CUeDJ4PEHxx+MFz4gAPl/8AZp+NfhX9jn9kf9pb4beNdP8AEGu6R/wTU+MHj79m7wZ4J8AWuna54g8YfDO80TwD8aP2AP2a/gRB4g1Xw/rnxY+ME37Ln7Rn7J37KnhbSfGV3Z/EL4r/ALUGnap4T/4ST4k6vr2k/FHx94B8A/iN4V/4Jl/H34heGP8AgoF+1N8H/hDc/tsfB/4fftbar44+Lvxv07SfhJ8Qv289N8afEPwl+3n4e+CfxD+NN9oninwx8H/gx8KfEv8AwT3+DP7NXwc8cajob2X7PHgLwi/gXQvFnjbwd+0v4zP2/wDE/wDYp/4WR+3F8N/2lb/X/P8AhlYfD/4f/wDC1/h1far5tr4z+Kf7Kvi34veIv2MvN8IzeFL7w/4i+H/g/wAQftd/tG/G7xn/AMJJryeI/D/7R3wO/YW+JPwq/wCEdvfhn46n8S/f9AH4g/tC/wDBW79ijxp8U/hJ+zx8J/8Agqf+yB8D/CXxC+H/AMZvih8S/wBqr4fftJ/sieM/Efw9/wCFPeI/ghoHg34MeDz8Wbj4jfBLwp8QPjfqfxh1LxTa+KPiX4L+I2/4WfAz4xeFPBvwzfxb4r0340fAz7//AGPfil478f6P8cfBfjnXf+Flf8M6/tAeJf2e/DP7Q0OmaPo1r+0fo/g7wJ8OPEOs+PLvTPCen2Hw/tfiB8NfiB4x8bfsv/Hpvhslh4Eu/wBo79n74wX2h+BPgf8Aarn9nz4Tc/8A8FKPEnhXwN+wZ+1V8SvHX7OXwf8A2tvBPwh+D/iX41+Mf2d/jvf6dpvwz+JfhX4LJD8VfEOn6pc6x8KvjVpB8QaNpHg+88UeALXVPhzq+nah8QtD8LWF9qvg62uZfGnh4/4J+/HbTvjh8AobWx+B/h/9m+T4K+II/gbP8E/CcXirRvCvw+07wp4L8Ga/4J0Dwz8P/ij8Gv2Zvjt8LPD9p8NvF3gpNG8CfHP9lr9nbxVDpwtvEnw+8EeMP2fPEnwX+NvxXAPt+iiigAr4g/ae8c/EzUfjL+zx+zB4H+JPiD9nLSP2gPD/AMb/ABJqP7S3hfQ/h74g8aWPir4JQfDXW/DH7OXwjs/jN4J8f/Bu3+MHxl8N+LfiH8Whf+M/A/xS1GP4BfswftD2nhL4Vf2vev8AHP4A/b9eP/Hfwn8AvHvwz1TwL+054Z+D/jT4N+NPEHgDwnrXg7476N4L8R/DPxZ4q8R/ELwto/ws8M6p4e+INteeFte8Qa98VrzwTpfgDRruzutR1T4hXXhax8O20/iSfSYmAPzh+AX/AAUz8JaZ/wALq+F3xe0f9r/4u3v7Pv7QHxH/AGe/C37Rvw0/4Jx/txfEfw5+0bo/wm/sbw34r8ealf8A7PH7LHij4P6Z8QPh/wDGCL4n/s3/ABZb4f6hpfgTx18U/gX4y+MHw38CfCr4ZfErwX8KvBR4u+KX7R3hTx34d/4KG+O9d+IHgf8AZL0T4gQfCG6/Zx8VaZdeB4/Bv7Dvxb0f4daRqH7b/wAbfhrqun6PrXgT9oDwJ+01o+gfFrxz4i+OXxH0Twl+yv8A8EqLf4r3Xjf4F/CT9rS4+NfhCb9XvCfhPwr4C8K+GfAvgXwz4f8ABfgnwX4f0bwn4O8HeE9G07w54V8J+FfDmnW2j+HvDPhnw9o9tZ6RoPh/QtIs7PS9G0bS7O107S9OtbaxsbaC2giiU8WeE/Cvj3wr4m8C+OvDPh/xp4J8aeH9Z8J+MfB3izRtO8R+FfFnhXxHp1zo/iHwz4m8PaxbXmka94f13SLy80vWdG1SzutO1TTrq5sb62ntp5YmAPyh/aj+KX7R3i347eOfiP8As3678QNQ+GX/AAS4/wCEZ8V/Gn4G/D/TLrxBfftm/F34jeDvD3jv4x/s8R+CNK0/R/iL4t+IH7P/AOwL47j+J37MfgvR/EB+Cfx6/bJ/ay/Zwbxv4p0S9/ZI8caBd+v/ALb3xJ1H42fALwP+zv8Asr+Nvg/4n+In/BQnw/qPgv4YfEbxF4G8K/tN/BDw1+zVrfgtfFHx2/ag8XfDVdcfw38VPg/o3wb1a28F/Dq+1m28S/BDxx+0r8dP2VvhV8V3i+Hfxnur8/UH7Ln7N/gT9kj4E+BvgD8OtY+IHijw/wCDP+Em1PUPG3xZ8b6x8SPin8RvHfxA8Y+IfiT8Uvil8S/HOuyNe+JPiB8Ufib4v8XfELxlqEFvpmjnxH4l1KHw7oXh/wAPxaZoen+P/szfsQ+Ff2bPiF4x8a2PjjxB430i38P6j8L/ANnPwT4g07TofD/7LXwC1z4meMPjRrnwb+FMELT23hzw/deNvGml/D61svAtj8PvBdv+y/8As1/sNfA288A6lq/7Llv8UfiAAfyRfBnwb+31oXjHQfhvN8WPiB+yT/wT4/Zs/ZA/4KJeL/iF+2Toum/Gj4xfEX9gT9ja/wDjt+zp4f8A2nf+CT/7P/xpu/hprmmeKv2v/wBhr42/sGfGD4EfCn9oe78efHG+8Q/ssa7F+0L8BfCWl3Hgn4J/Dy2/f7/glp8LfHf7CWseA/2LPG+hf8IV4S/aI/Z/8aftkfBj4EWOp6P4mtf2LdY+G/jv4YeAPj3+xzF4p8OahF4S8T/D/wCE/hL49/siad4M+LehWvi7x3+1Z+0daft0/ta/Hfxbpvi34y+GNL1P3/4l/sdeO/FH7ZOm6lpF55X7Ivxh+IHwn/bF/aT8M/Z9Hf8AtP8Aax/YxsfBvhP4G2f9s3Xie3+Jtl/wuC90T9kb4t/aPAUemfDb4f8A/DrX/hAvF/hjxTD+258TbmX6A/bW/Y68Cfts/CzQPhd47vP7MstE+IGleIpNQ+z6xe/bfAnijw54r+Cn7SHw6+y6P4n8KTW3/C//ANkX4uftCfs3/wDCXLqEusfCr/hcH/C4PAcFv8Tfh/4I1XTQD4A/Z9+KXjvW/wBrH4Aftw6vrvm/BL/gqN/wtX9nv4N+DtP0zR59Yg+EXwn+G2tftM/8E3/Hmp6jcafomp2/w/8AHHwS+En/AAUV/ao11tVs/DHxs8D+O/8AgoP8Lf2aPix4E8caZ8BNF8YfCTn/ANsnxZ4q+IvxC8Y/tv8AhrxN4g0H4Hf8EmvjB8LIfDviHSNZ1F/Bevz2fxM8Cxf8Ffvj9qvg6G58Q+Afjv4f/Zv/AGAta+L/AOyt8J7jQNPvPjL8M/j7cf8ABRX4V6F8Pb7446D8E9Y0f9P/ANsn4KeKvj9+zx4x8C/DzUPD+m/FbQvEHws+NfwSuPGd1qNn8PZPj7+zX8W/Av7RnwE0/wCKk2h6VrPiR/g/q3xk+FfgfS/i9a+ErOHxpffDO88V2PgzVdB8U3Gka5p3f/AH4KeFf2dPg18Pfgr4O1DxBr2keAvD8Om3njHxndadqnxC+JPiq8nuNY8dfFv4qeIdL0rQ7bxj8YPi9421LxD8Tvi949l0qz1Hx/8AEzxZ4r8aaxG2r67fSyAHwB+0L/wWp/4Jt/Bz4BfHD4u+Bf23v2IPjZ42+Ffwf+JfxH8HfBnwn+2X8Bk8VfFzxV4H8F614n8PfDHwy+j+J/Fmrr4g8e6vpdn4V0ZtL8K+JdRXUdWtjY+H9ZuRFp1z8QfB3/grP8Nvhj8aLW9+MH/BSH9n/wCOnwF+J/7X/jD9kyf4meLfid+yd8O/gToOseDf2Bfh9+3B4i+Pv7LPir4daL4avfD/AOz/AODPib8SIf2L/Gnwg+PXxf8A2ufHdh4x8Zfs/axd/ta6D460zxd4F+Pf9D3iy58VWfhXxNeeBdG8P+I/G1r4f1m58HeHvFnibUfBfhXXfFUGnXMvh7RvE3jHR/Cfj3V/Cfh/VNXWzsdZ8TaX4F8aajoWnT3OqWPhPxHc2sWj3n5A/wDBHj9pH4NftV+Ffip8dvBf7Dnwf/Yv+K3xx8P/AAV/aJ+KMvw40OfSfFXxq8P/AB207x54x8CeOvidrHj39nH9lD4yfE7xBF4kX4qsvxktfhh8Sf2X/iHqOreILr9nf9qv44+KdO+PXh74TAH6/eE/FnhXx74V8M+OvAvibw/408E+NPD+jeLPB3jHwnrOneI/Cvizwr4j0621jw94m8M+IdHubzSNe8P67pF5Z6po2s6XeXWnapp11bX1jcz208UrdBX5wfBbwn4V/Y6/a4sP2RPhB4Z8P+G/2fP2kfg/8cv2qfhz8MfC+jad4J8F/sweKv2dtb/ZA+CvxK+HXwj8F+F7ax8E6V8H/jlc/Hrw18ah4R0Lw14U1HwZ8fbX9of4j6/4i+KMn7SFhpXwY/R+gAooooA/GG8/4KS+Kvhl8Gv2dv8AgoH+0H8Rf2YPhp+wf+114g/Z90X4XfDDxPb6j8OP2h/hl4V/aon0Ffgv8S/GHx28bfGh/g38VPEGjeG9W074r/tJ/A7w78Ifhjp3wF+Elx8afF3hT9oX492H7LUF1+0r8Qf8Fm/DX7LH/BZf9nHwp8Bf+Cfv7Wv7P/xj/b68NfECy/4UZqv7OXx5+HXjPWPBPws+LNq/wc/a6/4X744+E8HxE8Z/DD9kDXv2cvGXjOb4yefd+E/DnxU8d+H/人工智能KfB+P/人工智能WR8RfG3w0+C3xK/b7wj4//AGWNX/aO8RfsueGfBXw/tfib8AvP/aX0r7J4c+HUGj6R8U/jXdfEX/hderfD3+z72XxBYftAeHfD/wAcdG8c/tO39t4e0bxHpHgT9vP4J+JvFmvarZftR2v9r/X9AH4g/wDBPL/hVn/BNn/gn3+0F4Q8Yf8ACwPiJ8YP2Tv2gPj7pv7Vmuzf8I54x/aO/bA/an+InifSvil8MvGVpqZ/4Ruy+Ln7QH7cfwy+Mf7M2r/AX4aaj49+InxF0G6+MXwf/ZG8Y/Fjx38YPh34g1CX6/8A2GPil+0dc/8AC0f2cP219d+H/iP9rr4M/wDCE/FLxd4m+E+mXWkfCzxt8Iv2mP8AhLvFnw6134aaNPp63vhv4f8Awt+JvhD9oD9jrwbpnj7XdU+Nnjbw5+yfpv7QfxT0/QZvjr4dtrnoPix+xD4V+LH7XHwe/ah1Hxx4g0bSPAXh/RLb4o/Bmy07TtU8F/tGeKvg3rfjLxP+x3rPxQfxE2r21t4f/ZJ8bfGn9oP4weAfDPhTQ9E1HxB8ffFnwb+L3iLxY+r/ALM/wu06E/bC/Zy+MvxW1H4b/Fb9l74q+H/gd+0j8OvD/wAYvhJpPxN8TeG4PGenWHwa/aQ8K6VoPxBjtvC+tWHiHwtqHiD4afFbwN+zx+1h4T03U/C7T/E/xV+y/o37N2q+PfhP8Lvj38U/HukgHn/wb/be8VfEf9rjx98L/EPgfw/4b/Zp8U+IPih8Hv2QvjNa6jqMmo/GP4+/sg63e+GP2z/BvjhPEK+HLbwX4gg8bXXjHwb+zl8J9H0XxJ40+JXhX9iH9tb9omXW5PgtbfDTUbw/be+Nf7T9n4q8D/A39hvT/D/ij47eHPD+o/tXfF/w9rFr4fng174BfCDUVl8Nfsy2XjHX9V/4Rb4GfGD/人工智能KA/Fa0tfgP8IPil8U/D174L0H4NeC/20Pi34SuLr4k/s9aFo956B8ZP2Q9Oi/ZH8A/Ar9lqy8P/Dbxt+yh4f8AhfrP7D154n17xVL4f+HHxC/Z00Sy0v4N+E/GHjoReLPisvwf8e+FtLuv2ef2k7nw3qcnxM+I/wCy/wDE740/DpPEy3Pj/Ur6U/Yh8J+Kta8K+OP2rfit4Z8QeFfjJ+2H4g074o3Xg7xvo2o6H44+CvwC0vTm0f8AZa/Zv13w94ktpfFPw48QfDj4Uy2/j347/B+TxH4n8F+D/wBtr4yftd+Kfh3qEfhv4hpEQDz/APaG+P2nftF/AL9nz4efsr/ELxAmr/8ABSPw/wCHj8MPiv4Im8VeCPHHw2/ZH8WeC9M+Inx2/as0K4W3034k/CHxB4O+BOuW3hL4EfE3WfA+qaJ4A/ba+Nn7Ingz4r+H9O0jx7dRxnhP9t7xVZ/8E6vDP7UvjrwP4f8AEf7SNr4f0b4LeMfgV4T1HUfBfhXXf+CisHxQtv2SfEP7KnhnxnrC+PbDwn4f1T9vBbz9nfRvi7qmr+NPhfoWnT23xQvvH/iP4XWsvju86D9k39in/hnP4p/F7xhqev8A/CR+EtL+0fCf9jrwtPqv9sWP7Pv7LGveI7v46eJ/hp4V0S48KaHpnwo8z42+Ptd+DumeDfhbdR/Dpv2Nv2Tf+Cevw91DTZvFvwIvNXvPP/AH7HXjvRv27PGvjvXrzd+yx4I+IHiT9sX9n/whZ2+j6V4c0L9rH9pD4O2f7OPxWs/DmkaL4nXxB4b/AOFXeH/CH7S/xy8a3F/oFt8Nv2ivin/wVb8f+N9W8MH4z/s8y/ErxYAdB/wTvuvjL4Eg/aR/ZV/aI+NfiD4//Fb9m/4weHbqx+MfxC0qDwn8TPjf8Pf2gfg18NvjzqnxruPBFnqE+h+HPg/dftR+NP2rPgN8AdK8AafZfDP4e/D39naH9nzQdQ8SeKfgV461++8//b9/bp+IX7Ps/wAXNJ+F114f8CaR+y/8H/gH+0h+038X/GP7OfxM/a1g8J/Br9of4y/E34LeGdQ8H/s/fBr41fAXxt4g8P8Awytvgx8aPjx+0z8UZ/iTBP8ABj4NfC/Tj4J+D/x51f4i69d/BX7A+Nf7EX7F/wC0p4q0/wAdftGfsifswfH7xtpPh+18J6X4x+NfwC+FPxU8Vab4VsdR1XWLHwzp/iHx14T17V7Pw/Z6vruuapa6Nb3kenW+o6zqt9DbJc6jeSzfzw6X+x//AMEXv+CxngT9qL9kv4c/8E4fh/8AsW/Hr4N/8Lc8LQ+PPDvwj/ZS8N+O/gV8dvAusfEr9nuTV/iKv/BP39orxRe6Z/wr/wCJsV94m8I/Av8Aal8Y/DHwd+1bo/huf4h/BDRPjJ4F+GnjPx38OgD+j79mL46f8NFfCK0+Itz4W/4QrxBpnxA+Nnwd8eeFoNb/AOEo0fRvin+zl8bPiF+zx8W7Xwj4rk0jw3e+L/h+3xN+F3iyf4deMNZ8I+BfEfizwJL4d8ReJvh78P8AxBqepeC9C9/r84P+CePxH+CHhP4Z+Ff2LvBnwx+MH7Nvjb9nTw/4x8E2nwA+N7ftK+I4E8K/CX4hXfw88Ra5+zD+0B+054f0fV/2tP2YPDOr33hJvhr8Sfh5qepad4C+DXxK/Z40Pxx4G+A1z418E/CfS/0foAKKKKACvyB+L/7fPxT+HHwi+PP7fNz4g/Z/8GfsMfstfED47/Djx78KPiJ4e8R2X7R3xg/4Zl+NnjP9nH4teJvh/wDHGT4weH/g/wDDf4geJfjB4M8WeH/2Yf2ddZ+D/wAUv+Ggrrw98K/D3ib4+fAfxR+0pqWm/sy/r9XyB4u8f/ssaR+0d4d/Zc8TeCvh/dfE34++R+0vqv2vw58Op9H1f4p/BS6+HX/ClNW+IX9oXsXiC/8A2gPEXh/4Haz45/Ziv7nw9rPiPV/An7Bnxs8TeE9e0qy/Zcuv7IAPH/Fn/BVH9i/VvCvibTv2V/2k/wBmD9sv9pG68P6zH8D/ANlr4EftMfCnxp8TPjj8TBp1y/hLwFpdr4E1Xx7q/hPw/qmrrbP4/wDi3rPhi5+HvwO+HsHin4zfFfUvDnwu8B+MPEmk9B+zh8dfHfw//wCGnPg9+2v8W/h/qXxN/Zb8v46+Lvjv/w人工智能/o/wR+Fnij9k743/APCwPH/w6+Lf/CLT+JfF/h/4I/D/AOEniDwD+0B+y5/wj/j74xePviTL4c/ZM/4X78U/EqWXxk8O6pqf3/XxB+13+xD4V/a48VfAjxFrnjjxB4Gtvhn4g13Qfippegadp2sQftCfsweNtR8EeOvit+yH43sfEjaj4Wtfg/8AHb4rfBH9nTUfjlLN4U13xB47+DXw68d/s+W97oHgn46fEO8nAPH/ANin9pD9o7xf8U9f8GftY6P/AMIje/tPfD/Vf21P2OvBN74Iuvh54x+Fv7OOneI/Cnw28T/sufF3wNcR6z4g0L9oD9nXw/4s/Zf+Kn7Rfibx/wCK1tfEnx2/bL+Inwh+B+nav8Mv2ZLzXF6DxN+294q0P9tq2+Dsfgfw+f2TvC3iDwn+zJ8Wfj5LqOox+IPB37efxq8D6N8cPgx8Lde07V18OeG/Bfwfg+Dd18O/Cl78TLjUPGD/ABe/ag/be/ZD/Z++FFnH4x0b4w2Wm/QH7VPwU8VfFzwr8OvEvwu1Dw/o/wAdv2evjB4R+PnwN1TxZdajZeFbnxVoGneIvAvxB+Hvia+sdK8Ux6D4f+Pn7PnxD+NH7OOs/EGfwB8TNR+DmnfF+5+NXgn4eeKPiT8OvBVmvn/hn9iHwrH+xLc/se+PfHHiDxDq/izw/wCLNe+JXx88Gadp3gL4haj+0/8AEvxxrPxw+I37Xnwr06/bxxofwT+MB/aj8S69+0z8IYvC6ah4f+APxMXwo3wystL0jwN4XsrEAP23viT8ZbHwr4H/AGd/2V/G3h/4fftY/tQ+INR8F/DD4jeIvA0HxV0T4A/D3wppy+KPjt+1B4u+Gq65pNzrPh/4V+CEtvBfw6vtZttQ+Geo/tcfF/8AZW+FXxXfTPB3xZur+Pz/AFn9t7xV4j/Yl8J/GL4c+B/D+hftY/GDxBc/syfDn4B+J9R1H4geH/Bf7edn448TfA/4lfC3xhqPhdfBviT4q/B/9k34yeBfiz4r/aT+Jnwb0+8ef9l/4AfGn9oH4aWfiDwdoNhe3R+xD4T+PvxF8VeOP2rf2wPDPh/w18dk8P6d+yt4N8HeGtG8aaN4H8DeFfgnqLaP+0T8Rfhh4e+KFtfeMfDPh/8Aa0/ax0fx/wCPfCfi7SvEY0748fsS/Cv/人工智能J2eKfHPh3SfiT4H1qKLoPAH7FP/CHftk+NfjpPr/2z4JWf/CSfFj4H/B19V+0eHPhr+1P+0FY2fg/9qf4l6P8AD1/Clr4S8Hfb/CXw18O+Kfhh4y8I6uvxFuvin+2j/wAFOtb+Iupa1pn7Rlja2AB5/wDAn4peBPCX7Dv7THgD9tPXf+E48JfsI/8ADRn7Pf7VmpfF/TNY+NWseLf2cfhJ4SufHvwy8efHmQ6f4xt/jt8QPjt/wT48Y/Ab47/HdvC+l63a+LfHfxW8Z+FrvwJ4Q8W2/iD4SeEvzg/4N+/2ZPj7/wAE8PFX7X37Gvx0+Fvwf/Z98E/GvxB4b/4KIfssfBPwT8TPGnxf8VfDnwr8Z9R8R/Cv4y/s3a58Y/GFnoekfGvxB+xtpHwv/Zi8JfEnxF8OrDxZp2gaj8afA3inxV8SfEdt8avh9Dafo/8AFv8AY68d+O/24vDXi+wvPsv7KXxL/wCFFfHr9onwnp9vo+maPrH7R37B/i3xBrP7Ps2p21n4n0rxbffED40eLfiN+zl8Std+MHhvSI7rR/An/BJ/4W/s4/FW7+IHws+Neg+GfAn2B8dP2Tv2WP2oP+EW/wCGl/2af2f/ANoj/hB/7b/4Qr/henwb+HXxb/4Q/wD4Sb+yP+Ek/wCEW/4T/wAOeIP+Ef8A+Eg/4R/Qf7b/ALJ+yf2r/Ymkfb/tH9m2fkgHj/7WP7Q/xC+HvirwV8D/人工智能Lnw/ofxW8efB/4/wD7Q9x8RfG3wj+Jn7QfhXwJ8Gv2XNR+DGmfEw6H+zz8EPFHg34yftBfGDxf4k+Pfwu8H/Db4R+CfFvgie+07V/HPjuDxR4i8U/D7wh8Cvjf8wfs9/8ABXH4YeNdH8eeE/ix8Mv2v/8AhbXwS+IDfCj4j6v8Lf8Agl//AMFNdT8CeLtY/wCEE8CfErw/450Lwgv7Mvi74gfBr/hNfh/8SPBvibU/gl8Ybn/hO/hvrGp6ho2ieKvjb8Jf+FY/tHfGXz/9vz/gmt/wR3+Fv7G37QnxU+KX/BKn9n/xn8MvhV8P7z4pfEXQ/wBlz4G/A34JfHZfAnw3vrDxt4u13wN8SfDvif8AZ18QaN/wifh/QtQ8V+JtM0L4veGtY8X+DtF8Q+DNM0/xle+IIPA3iT7f/wCCePxe+AXxn/Zf8K+I/wBmrwZ4g8D/AAu0nxB4x0CDTvEHivwX8VJ9b8VHxBd+IvG3jdv2g/hd8VPj38Kf2l/EHj3xT4h1Txf8Tvjl4G+P/wAbNR8S/GXWfiPonxo8dp+0j4a+NHhTwwAewfs9/tO/CL9qDR/Hms/CS7+IH/Fr/iA3wt+IXh/4pfBP42fs/wDjvwf47/4QTwJ8TodC134cfH74e/DL4gWX234f/E3wH4s0zU5PDP8AY+q6P4m0+503ULv/AEhYff6/OD4QeE/Cvhz/人工智能Kv/t66x4e8M+H9B1fx7+xB/wAEyvFnjrVNG0bTtL1Hxp4qs/jB/wAFPPAtn4m8WX1jbQXPiPxBa+CfBfg7wdbazrEt5qMHhXwn4Z8PRXK6RoOl2dr+j9ABRRRQAV+MPwY/Yi/a48C/8FUPit+3N4q1n4P3Xwb+L3iD9p/wpcfCnS/ivrepaj8N/h740+C3/BNH4d/Cn4veFreT9lfwzq/ir4wfFDV/+Cf5s/jv8K/FXxYg+Gfwt8K654AvfhF4z8Y+JPDnxEk+Kn7PUUAFFFFABXP3PizwrZ+KtG8C3nibw/a+NvEfh/xN4s8PeDrnWdOg8Va74V8F6j4T0fxj4m0bw9Lcrq+qeH/Cer+PfAul+JtZsbOfTtB1Hxp4TsdUubW58R6PFedBX84P7RHx3+Lunf8ABXrwv8XtD+EH7QGsfsy/sx/tAfsN/sLfFj4t6F40+Cdj4E8K+O/2pvhP+0LpvjLwZp/gLW/jzoXxa1n4f/E74tf8FF/+CRXjP4pS6B8K77R/FWsfss6Z4r8RWOsa1+zH8HpNRAP6PqKKKACiiigDwD9qr9nvR/2sv2cfjR+zN4m8efED4a+Evjv8P9f+FvjbxZ8LW8CR+O4fAnjG1OjeOdC0K5+JPgT4leErD/hMfCV1rPg7U9TufB9/rGl6Pr+oaj4T1Dw54ttdD8TaOfs9/s96P+z/AKP48VfHnxA+LfxA+LfxAb4pfGH4w/FJvAlv47+KHju38CeBPhPomu67onwn8CfCz4S+HP8AhHPhL8LPhj8ONM0z4cfDHwPo93o/gfT/ABB4g0/W/iBrfjLxl4m9/ooAKKKKACvxh/4LXfBj9tr9on4GfDP4S/sQeGPEFx43TxB8dvid4j8dJ4j8D6N4L8N6j4A/Y9/aJsfgB4fvrPW/j38FPGI+MGs/tY+MPgL44/Zf+I/h208W+Ff2b/j78K/Bf7T/人工智能5bSbn4NeENL8Wfs9RQBz/hPWdR8R+FfDPiHWPCfiDwFq+veH9G1nVPAviy58K3nirwXqOqadbX194T8TXngXxN408E3XiDw5czy6PrNz4O8Y+LPCs+o2dzL4e8Ta7pDWeqXXQUUUAFFFFAH4A/sxf8FC/2p/if8SbTwBqX7SH7AH7Q3xg8L/tf/Gz9nD4sfsSfs9/Ab4i/D/8AaO8G/Cz4K/tY/EL9nDxl+05488ba3+3b8ebL4BfD/wAK/DLwXH+1A0fxb+B6eHPiJdan4E/ZO8BfECX4wfHT4PeKte/f6vxB+EP7Jv7fUvhL4f8Awh+Lfw6/ZA+GHh/wt+3/APEj9ue2/aD+EP7Vfxo+K3xd+H//AAsT9uL4n/tg+LPhd8P/人工智能b+Jv2JPgVZTf8ACzfhl8UvHv7EHxI8bR/HTwb/AGn8E/it8T/EWpeEfFPh/XtZ+BXij9vqACiiigDn/Fmjaj4j8K+JvD2j+LPEHgLV9e8P6zo2l+OvCdt4VvPFXgvUdU065sbHxZ4Zs/HXhnxp4JuvEHhy5ni1jRrbxj4O8WeFZ9Rs7aLxD4Z13SGvNLuvkD9ir9hD4e/sR+Fbbw94X+Jfxg+Mmr6X8H/gZ+zroHjr413nwzbxV4e/Z4/Zn07xlY/Ab4M6fZ/Bz4X/AAc8E3nh/wCHFz8SvibrFr4v17wdrPxb8U6j491WLx78RvFmkaJ4I0vwp9v0UAfmB+0x4A/4V/8At7f8E1/jp4P8a/EDS/EHxS/aA/ad/Zo+JPhbUPEf/CX+BPFHws+Lv7B/jf46a5pOmaJ45svE178L/wCx/ib/AME3/wBmzxToVh8FtX+GvhyXWF+KWt+J9B8SeIPiz421fU/0/rwD4yfAv/hbfxF/ZO8f/wDCU/8ACP8A/DL/AO0B4j+On9k/2J/av/Ccf8JB+yx+0t+zR/wi32/+19N/4Rn7J/w0R/wmv9t/Y/EH2j/hD/8AhHP7Ih/4SD+3tE9/oAKKKKAPyg+FP/BOH4hfDb/gor8Qv+Cg95+0Z4f8Q6v8WfEH7QWl+PPhTH8KviZp/hWP4NfEv4X/ALEfw7+EvhbwFb6l+0/4k8E+A/jB8O7n9hzwLrXxb+O9j8NNQn/aL07xXqXhLVPAHw+0jwN8I5PAH6v0UUAFeP8Ax3+NfhX9nz4Z6p8TfFun+INctoPEHgDwN4a8K+E7XTrrxV48+Jnxe+IXhb4RfCD4beGTruq+HvC2n+IPiX8VvHPgzwFo2ueOPFHg74e+HdR8R22vfEPxt4L8E6br/irSPYK+YP2wvgp4q+PnwQbwZ4F1Dw/ZeNvCvxg/Zn+Png608WXWo6X4V8U+Kv2WP2lfhJ+054e+HvibxFo+leItX8F+H/iZq/wis/h5rPxB0vwl461H4ead4nufHFj8PPiHc+H4vBOvAHn/AMJvjX+2hefH3w58Iv2jP2Tfg/8ADrwT4t+D/wAVfiPpfxm+Af7THxW/aH8K6F4q+GfjT4I+GLH4Y/EJPHX7F37M+keEfEHxH0j4u654q+HzW/irX9R13TvhL8QxD4f+zaPeajZ/b9fMHwU+Jf7Q/wAWfFWoeIfHX7PXiD9l34U6L4futGt/Avxr1r4SeMvj749+IV7qOlX0PizT7z9nP44/GX4N+APg/wCEvDdveaPa22qeMfGfxM+KvjTxRqst94Z+Bfhb4O6Hqn7Sn0/QAUUUUAFfmB+xr+wN8U/2f/iTb/FL45ftB/D/AONPiDwp/wANtf8ACtbP4Ufs/eI/gBo+j/8ADwr9rHw5+2L+0d/wnNv4v/aG/aNvfGv9mfE3wL4I0L4Jf2BqHw8/4QTwJbeKtM8d/wDC3PEHiHSPE/hL9P6KAPgD9vb/人工智能t/a/sxftK+Gf8AQvib8I/2v/2WfhPpV5H/AKNa+KPhZ+2z+0d8If2OvjX8NPG9xp/2LxBrfw/uPD/xg0b43aP4Ntte03w5L+0d8AP2b/iT4s03xXZfCq18Man9/wBef/FL4T/Cz44+BNd+Fvxr+Gnw/wDjB8MvFH9mf8JN8Ovil4N8OfEDwJ4i/sTWNP8AEWjf274R8Wabq/h/V/7I8QaRpWu6Z/aGn3H2DWNM0/U7Xyr2ytp4uf8Agp8OPFXwn8K6h4F134neIPip4b0bxBdR/CzVvHK6jq3xM8NfDN9O0o6L4C+JPxJ1bxBrOr/GrxB4P1ca/peh/FvxLZ6T8QvEvw9TwTY/F/Uvip8ZNG+IPx4+LAB7BRRRQAV+UHxW/wCCcPxC+JP/AAUV+Hv/AAUHs/2jPD/h7V/hN4g/Z90vwH8KZPhV8TNQ8KyfBr4afC/9tz4d/Frwt49t9N/af8N+CfHnxg+Ilz+3H461r4SfHe++Gmnz/s6ad4U03wlpfgD4g6R45+Lknj/9X6KACiiigD5A/wCCgfxi+Kf7Ov7Dv7Wf7Q/wUuvh/b/E39n/APZ/+KPx08MwfFLwf4j8d+BNZ/4U/wCEtT+Ius+Ftd8O+E/iF8LvEDf8Jf4f8N6r4W0zW9P8aWX/AAiesaxp/iu60jxbZaJc+Edd5/4TfFn4++B/j74c/Zc/ai8R/B/4o+Nvij8H/ir8fPhT8VvgH8KvGnwP8KxeFfgf40+CPw8+Knw9+IXwr+Ifxu/aC1fTPEGmav8AtBfCfxJ8PviD4b+LGvad8RdO174h+HPEfw8+Elz8JPDfiT48dB/wUD+DvxT/AGiv2Hf2s/2ePgpa/D+4+Jv7QH7P/wAUfgX4Zn+KXjDxH4E8CaN/wuDwlqfw61nxTrviLwn8Pfij4gX/人工智能RDw/4k1XxTpmiaf4Lvf+Es1jR9P8KXWr+ErLW7nxdoXP8Awm+E3x98cfH3w5+1H+1F4c+D/wALvG3wu+D/AMVfgH8KfhT8A/ir40+OHhWXwr8cPGnwR+IfxU+IXxC+KnxD+CP7Pur6n4g1PV/2ffhP4b+H3w+8N/CfQdO+HWnaD8Q/EfiP4h/Fu5+Lfhvw38BwD7fooooAKKKKAPmD9tb4B+Kv2q/2R/2jf2Y/B3xC8P8Awp1f9oX4P+OPgpefEPxN8PtR+KWneFvCvxP0S68GeOtQtvA+l/EP4V3OreIH8E6z4htPCd1L42sNO0DxVc6N4i1jSvFekaTfeEtcP2YvgH4q+CsHxo8VfEr4heH/人工智能mfGT9oz4wQfGv4v+JvA3w+1H4T/DM+KtH+DXwf/Z68Naf8Nvhpr/xD+MPinwf4ftPhT8BvhydctfFHxd+Iuo6z8QpvG3iqw1Xw94b1/QvAPg/6fooA/MD9qj4iWvwO/b6/ZA+Nfi74f/tAeKPhlp37IH7fnwt1jxN8C/2Yf2jv2m/+Ed8d/ED40f8ABN/xZ4I0LxTo37N/wr+K3iDwt/wlPh/4U/EXUNE1PxFpWmaPf/8ACI6vawag17FHbS/f/wAJ/il4E+OPws+Gnxr+Fuu/8JR8MvjB8P8Awb8Uvh14m/szWNE/4SLwJ8QPDmm+LPCOu/2N4i0/SPEGkf2v4f1fT9Q/szXdK0zWLD7R9l1PT7K9intovQK5/wAM+E/CvgvTrnR/B3hnw/4T0i88QeLPFl5pfhnRtO0HTrrxV498Vaz468deJrmx0u2tbafxB408beI/EPjHxZrMsTaj4j8Va7rPiHWLm81fVL68nAOgooooAKKKKACiiigAr5A8R/8ABPb9gXxj/wAJ/wD8Jd+w9+yB4q/4Wv8AECz+LHxS/wCEj/Zp+C+uf8LK+Kenf8Jr/Z/xL8f/ANp+Crr/人工智能TH4gWH/CyviL9j8ZeIv7R8R2v/AAn3jXyNST/hKtd+3lFAH1/RRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAH/2Q==" /> 

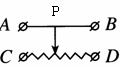
5. 如图2所示，要使滑动变阻器的滑片P向右移动时，电阻变大，应选择的接线柱是（     ）

A．A、D        B．B、C       C．A、B        D．C、D

6．为了改变一根导线电阻的大小，下列办法中一定不可以达到目的的是（      ）

A．将导线拉长后用                   B.将导线对折后用

C. 给导线加热                         D.改变导线中的电流

7．一导体接在某电路中，假如两端的电压增大到原来的2倍，下列说法正确的是（   ）

   A．电阻和电流都变成原来的2倍；    B．电阻不变，电流变成原来的1/2

   C．电阻不变，电流变成原来2倍；    D．电阻和电流都变成原来的1/2

8．如图3所示的变阻器四种不同接法的电路中，闭合开关后，当滑片向右移动时，

电路中灯泡变亮的是（   ）

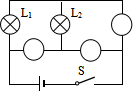
9．如图4所示，A、B是同种材料制成的电阻，它们的长度相等，A的横截面积是B的两倍，将它们串联在电路中，则加在A、B上的电压UA、UB和通过A、B的电流IA、IB间的关系正确的是（     ）

    A．IA=IB       B．IA >IB         C． UA=UB         D．  UA>UB

10．由欧姆定律导出公式R=U/I，下列说法中正确的是               〔     〕

A．导体的电阻和它两端的电压成正比            

B．导体的电阻和通过它的电流成反比

 C．当导体两端电压为零时，它的电阻也为零      

D．以上说法都不正确 

2、填空题

1．在电阻肯定的状况下，导体中的电流与____________成正比；在电压肯定的状况下，导体中的电流与__________________成反比。欧姆定律的内容是：导体中的电流与导体两端的____________成正比，与导体的________成反比，表达式为_______________。

2．伏安法测电阻是用____________测出电阻的电流，用___________测出导体两端的____________，依据_____________计算出电阻阻值。

3. 一段导体两端的电压是6V时，通过导体的电流是200mA，则该导体的阻值为

Ω；若使该导体两端电压变为3V，则该导体的电阻为__________Ω。若使该导体两端电压不加电压，则通过该导体的电流为__________，则该导体的电阻为__________Ω。[来源:学#科#网]

4．下图5是有4个接线柱的滑动变阻器，当AD端接入电路时，滑片P向右移动，接人电路中的阻值将__________；当AB端接入电路时，滑片P向左移动，接入电路中的阻值将 __________。若该变阻器铭牌标有“20Ω1A”字样，表示这个变阻器电阻变化范围是__________，允许通过的最大电流是__________A。滑片P移至中点时，接入电路的阻值是__________Ω。

5．如图7所示的电路，是表示滑动变阻器连入电路的四种接法。当滑片向左滑动的过程中，（1）电流表示数变大的是__________电路图；（2）电流表的示数变小的是__________电路图；（3）电流表的示数不变的是__________电路图；（4）不正确的连法是____________________电路图。

6.一段铜丝，对折起来后它的电阻到原来的________,这是由于它的_________变小，而____________变大的原故。

7. 有A、B、C、D四根导线，A是镍鉻合金线，其余三根是铜线；B、C粗细相同，C长B短；C、D长度相同，C粗D细；A、D长度、粗细均相同。则这四根导线的电阻关系是：B__________C__________D__________A。

8．某同学探究导体对电流的妨碍用途，所用器材为截面积相同的导体、电流表、电键、新干电池和导线若干，实验过程如图8（a）、（b）、（c）、（d）、（e）、（f）所示。请依据实验现象及有关条件，作出判断并总结得出初步结论。

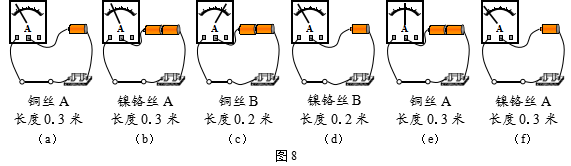
①由图8______________________________或______________________________，可得：不同材料的导体对电流的妨碍用途不同。

②由图8（c）与（e）或（d）与（f），可得：____________________。

3、作图题

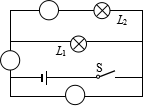
1．在图9和图10中的○里填上适合的电表符号，填上后需要两灯并联，电路能正常工作。

2．在图11所示的电路中，有三根导线尚未连接，请用笔线代替导线补上，补上后需要：当电键S闭合后，向左移动滑动变阻器的滑片时，电流表示数变大，灯L亮度变亮。

[来源:学科网]

4、计算题

1. 把一个电热器把它接在家庭电路上，通过它的电流是5A，该电热器的电阻是多少？

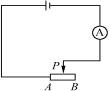
2. 如图12，电源电压不变，滑动变阻器的总阻值为20欧。当滑片P移到B端时时，电流表的示数为0.5安。当滑片P移到滑动变阻器的中点时，电流表的示数为多少？

5、实验题

1．某实验小组在“探究导体中的电流与电压的关系”时，由实验小组长选择了器材，若干节干电池、金属导体、电流表、电压表、____________和____________。讨论得到了可以通过改变电池的节数从而改变__________________。

（1）请在方框中画出实验电路图，并在图中标出电流表和电压表的“+”“-”接线柱。

（2）小组一同设计记录电流I与电压U的表格。

（3）由表格可以可以得到：__________________________________________________。

2．在温度肯定的条件下，做探究“决定电阻大小的原因”的实验，使用了控制变量的办法．下表是某次研究性学习小组的实验数据记录．依据实验数据的剖析，回答下列问题：

（1）选择B．E导体进行对比，是为了研究导体电阻大小与__________是不是有关系；

（2）为了研究导体电阻与横截面积的关系，应选择的两根导体是 __________和______________________________（填导体的代号）；

（3）比较表格中导体C．F对应的数据，可以得到的结论是__________．

3．如图13所示的电路中，闭合电键后，若要使滑动变阻器滑片向右移动时，电流表的示数变大，应将变阻器的__________和__________两个接线柱接入电路中。

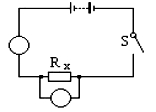假如一个同学在连接好电路后，闭合开关，发现如何移动滑片P，都不可以改变灯的亮度，你感觉可能是什么原因什么？____________________

4. 如图14所示的电路，可以测电阻Rx的阻值，需要： 

在图中○内，填上电流表和电压表的符号。

在图中标出电流表和电压表两端“+”“－”接线柱。

当电键S闭合时，电表的读数如图15所示，则电流表

的读数是______________________________安，电压表的读数是______________________________伏，

被测电阻Rx=____________________欧。