数学初二上 第十九章 几何证明
19.3 逆命题和逆定理（1）
1、选择题
1．下列说法中，
正确的是 （ ）
A．每个命题都有逆命题 B．假命题的逆命题肯定是假命题
C．每个定理都有逆定理 D．假命题没逆命题
2．下列命题的逆命题为真命题的是 （ ）
A．假如a=b，那样a2=b2 B．平行四边形是中心对称图形
C．两组对角分别相等的四边形是平行四边形 D．内错角相等
3．下列定理中，有逆定理的是 （ ）
A．四边形的内角和等于360° B．同角的余角相等
C．全等三角形对应角相等 D．在一个三角
形中，等边对等角
4、下列命题的逆命题是假命题的是
A.两直线平行，同位角相等 B.全等三角形的对应边相等
C.直角三角形两锐角互余 D.全等三角形对应角相等
5、下列的真命题中，它的逆命题也是真命题的有
①两直线平行，同旁内角互补；②等边三角形是锐角三角形；③若a=b，则a2=b2；
A.1个 B.2个 C.3个 D.4个
6．△ABC中，∠C=90°，∠A与∠B的平分线交于P点，则∠APB的度数为 （ ）
A. 150° B. 135° C. 120° D. 90°
7．下列命题的逆命题正确的是 （ ）
A、全等三角形的面积相等 B、全等三角形的对应角相等
C、等边三角形的三个角都等于60° D、直角都相等
8．下列定理中，没逆定理的是 （ ）
A、等腰三角形的两个底角相等 B、全等三角形的面积相等
C、同位角相等，两直线平行 D、三个内角都相等的三角形是等边三角形
2、填空题
9．在两个命题中，假如第一个命题的条件是第二个命题的结论，而第一个命题的结论是第二个命题的条件，那样这两个命题叫做______
__．
10．假如一个定理的逆命题能被证明是真命题，那样就叫它是原定理的________，这两个定理叫做_________．
11．每一个命题都有它的________，但每一个真命题的逆命题可能不是真命题．
12．线段垂直平分线性质定理的逆定理是__________ ．
13．命题“对顶角相等”的逆命题是_______
______________，是_____命题．
14．写出下面命题的逆命题，并判断其真伪．
|
| 真伪性 | 逆 命 题 | 真伪性 |
（1） | 假如x=2，那样（x-2）=0 |
|
|
|
（2） | 两个三角形全等则 |
|
|
|
（3） | 在一个三角形中，等边对等角 |
|
|
|
（4） | 等腰三角形是等边三角形 |
|
| [ |
（5） | 同旁内角互补 |
|
|
|
对应边相等 15. 说出下列命题的题设和结论，并说出它们的
逆命题：
①假如一个三角形是直角三角形，那样它的两个锐角互余；
题设是：__________________________结论是：__________________________________
逆命题是：________________________________
②等边三角形的每一个角都等于60°；
题设是：__________________________结论是：__________________________________
逆命题是：________________________________
③全等三角形的对应角相等；[
题设是：__________________________结论是：__________________________________
逆命题是：________________________________
概括：每个命题都有__________，一个真命题的逆命题________真命题，一个假命题的逆命题____________假命题.
16、如是一个定理的逆命题也是__________，那样称它们叫做_______________.其中的一个定理叫做另一个定理的_____________________.
17、等腰三角形的性质：假如一个三角形有两条边相等，那样这两条边所对的角也相等.它的逆命题是:_____________________________________________ ，这是_______命题，它们互为___________.
18、“两直线平行，内错角相等.”的逆定理是:_______________________________________.
19. 通过本节课的学习，大家认识了互逆命题与互逆定理，了解了每一个命题_______逆命题，但每一个定理________逆定理，了解了写出一个命题的逆命题的重点是正确找到它的___________。
20． 把命题“角平分线上任意一点到角的两边距离相等”改写出逆命题是__________.
21．如图，线段AB垂直平分线段CD，BD=4，则AC=__________
22．如图，AB=AC=14cm，DE垂直平分AB，若△BCD的周长为24cm，则BC=__________cm.
23．如图，△ABC，∠C=90°，∠B=15°，DE垂直平分AB，若BD=8cm，则AD=__________cm.
∠DAC=__________°.
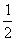
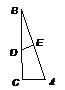
第21题 第22题 第23题 第24题
24．如图，△ABC，∠C=90°，DE垂直平分AB，若∠CBD=40°，则∠A=__________度.
25. 已知:AD是△ABC的中线,则S
____________S.．
26．Rt△ABC中，∠ACB=90°，∠A=48°，则∠B=__________.
27．如图所示∠C=90°，AD平分∠BAC，∠CDA=64°，则∠B=__________.
28． 如图所示∠C=90°，AD平分∠BAC，CD=5，求D到AB的距离________.
第27题 第28题 第29题 第30题
29．如图所示，PA⊥OA于A，PB⊥OB于B，且PA=PB，则P在__________.若PC=PD，则点P在__________.
30．正方形ABCD的边长为4，AE是∠CAB的平分线交BC于E，若BE：CE=1：2，则点E到AC的距离为__________.
31.命题“等腰三角形的两个底角相等”的逆命题是__________。
3、简答卷
32、写出下列命题的逆命题，并举例说明下列命题的逆命题是假命题：
①假如一个整数的个位数字是5，那样这个整数能被5整除；
②假如两个角都是直角，那样这两个角相等．
33、写出下列命题的逆命题，并判断真伪：
（1）假如∠α与∠β是邻补角，那样∠α+∠β=180°；
（2）假如一个三角形的两个内角相等，那样这两个内角所对的边相等．
34．已知：如图所示，在△ABC中，∠C=90°，AB的垂直平分线交BC于D，
①若∠CAD=16°，求∠B的度数;
②若∠CAB=52°，求∠CAD的度数;
③若∠CAD：∠DAB=1：2，求∠B的度数.
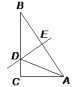
35. 已知：如图所示，在△ABC中，∠C=90°，∠A=30°,DE垂直平分AB于D,交AC于E,求证：DE=CE.
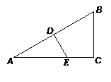
36．已知：如图所示，△ABC中，D为BC上一点，AB=AC， ED=DF，求证：BE=CF.
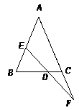
37．如图，在△ABC中，E、F分别是AB、AC上的点。①AD平分∠BAC；,②DE⊥AB,DF⊥AC,
③AD⊥EF,以此三个中的两个为条件,另一个为结论,可构成三个命题即①②→③,①③→②,②③→①.
（1）试判断上述三个命题是不是正确（直接作答）
（2）请证明你觉得正确的命题（详证）
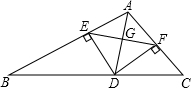
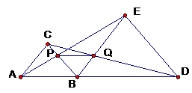
38. 如图, 已知: B是线段AD上的一点, △ABC、△BDE均为等边三角形. AE交BC于P,CD交BE于
Q.
求证：（1）△ABE≌△CBD.
（2）△BDQ≌△BEP.
（3）PQ∥AD.
数学初二上 第十九章 几何证明
19.3 逆命题和逆定理（1）
参考答案
1. A 2. C 3. D 4. D 5. A 6. B 7. C 8．B
9. 互逆命题
10. 逆定理，互逆定理
11. 逆命题
12. 到一条线段的两个端点的距离相等的点，在这条线段的垂直平分线上
13. 假如两个角相等，那样它们是对顶角；假
14. （1）真，假如x（x-2）=0，那样x=2；假
（2）真，三边对应相等的两个三角形全等；真
（3）真，在一个三角形中，等角对等边；真
（4）真，等边三角形是等腰三角形；假
（5）假，假如两个角互补，那样这两个角是同旁内角；假
15. ① _一个三角形是直角三角形__ 它的两个锐角互余
假如一个三角形的两个锐角互余，那样这个三角形是直角三角形
② 等边三角形 它的每一个角都等于60°；
假如三角形的每一个角都等于60°，那样它是等边三角形
③ 全等三角形的对应角相等；[
两个三角形全等 它们的对应角相等
假如两个三角形的对应角相等，那样这两个三角形全等
概括：逆命题 可能不是 可能不是
16. 真命题 互逆定理 逆定理
17. 假如一个三角形有两个角相等，那样这两个角所对的边也相等. 等角对等边
真 逆定理
18.内错角相等，两直线平行
19. 肯定有 可能没有 题设和结论
20. 在一个角的内部（包含顶点）且到角的两边距离相等的点，在这个角的平分线上
21．4
22．10.
23．8 60
24．24
25. ＝
26．42°
27．38º
28． 5
29．∠AOB的平分线上 线段CD的垂直平分线上
30．
31. 假如一个三角形有两个角相等，那样这个三角形是等腰三角形
3、简答卷
32、举例说明下列命题的逆命题是假命题：
①假如一个整数能被5整除，那样这个整数的个位数字是5；
②假如两个角都是直角，那样这两个角相等．
33、写出下列命题的逆命题，并判断真伪：
（1）假如∠α与∠β是邻补角，那样∠α+∠β=180°；
（2）假如一个三角形的两个内角相等，那样这两个内角所对的边相等．
34．①∠B的度数为37°;
②∠CAD的度数14º;
③若∠CAD：∠DAB=1：2，求∠B的度数为36º.
35.证明略，提示：联结BE
36．证明略，提示：作 EG//AC交BC于点G
37. （1）①②⇒③，正确；①③⇒②，错误，不符合三角形的断定；②③⇒①，正确．
（2）先证①②⇒③．如图．
∵AD平分∠BAC，DE⊥AB，DF⊥AC，AD=AD，
∴Rt△ADE≌Rt△ADF．
∴DE=DF，∠ADE=∠ADF．
设AD与EF交于G，则△DEG≌△DFG，
∴∠DGE=∠DGF．
∴∠DGE=∠DGF=90°．
∴AD⊥EF．
再证②③⇒①．如图2，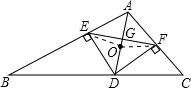
设AD的中点为O，连接OE，OF，
∵DE⊥AB，DF⊥AC，
∴OE，OF分别是Rt△ADE，Rt△ADF斜边上的中线．
∴OE=AD，OF=AD．
∴OE=OF．
∵EF⊥AD，
∴△OEG和△OFG为直角三角形．
在Rt△OEG和Rt△OFG中
∴△OEG≌△∠OFG
∴EG=FG
在△AEG和△AFG中
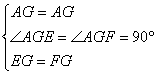
∴△AEG≌△∠AFG
∴∠EAG=∠FAG
即AD平分∠BAC．
38.（1）略，提示：借助S.A.S
（2）略, 提示：借助A.S.A
（3）略，提示：证明△BPQ为等边三角形
