第一学期上大附中期末考试
高二 数学试题
1、 填空题(共36分)
1. ![]() __________.
__________.
2. 双曲线![]() 的渐近线方程是__________.
的渐近线方程是__________.
__________
3. 已知矩阵![]() ,则
,则![]() __________.
__________.
4.已知![]() ,
,![]() ,若
,若![]() ,则实数
,则实数![]() __________.
__________.
__________
5. 行列式 中,第2行第1列元素的代数余子式的值为
中,第2行第1列元素的代数余子式的值为![]() ,则实数
,则实数![]() __________.
__________.
6. 已知直线![]() :
:![]() 与
与![]() :
:![]() 平行,则k的值是__________.
平行,则k的值是__________.
7.若向量![]() 的夹角为
的夹角为![]() ,
,![]() ,则
,则![]() __________.
__________.
8.已知实数![]() 、
、![]() 满足条件
满足条件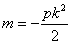 ,则
,则![]() 的最大值为__________.
的最大值为__________.
9.曲线C的方程是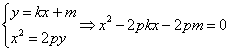 ,则曲线C被坐标轴所截的线段长
,则曲线C被坐标轴所截的线段长![]() __________.
__________.
10. 椭圆![]() 上一点
上一点![]() 到焦点
到焦点![]() 的距离为4,
的距离为4,![]() 为原点,
为原点,![]() 为
为![]() 的中点,则
的中点,则![]() __________.
__________.
11.设![]() 是曲线
是曲线![]() 上的点,
上的点,![]() ,
,![]() ,则
,则![]()
的最大值为__________.
12、已知各项均为正数的数列![]() 满足
满足![]() (
(![]() ),且
),且![]() ,则首项
,则首项![]() 所大概取值中最大值为__________.
所大概取值中最大值为__________.
2、 选择题(每题4分,共16分)
13. 已知复数![]() (
(![]() 为虚数单位),在复平面内,
为虚数单位),在复平面内,![]() 对应的点在( )
对应的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
14. 在平行四边形ABCD中,下列结论中错误的是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
![]()
15.已知![]() ,
,![]() ,则
,则![]() 对应的点
对应的点![]() 的轨迹为( )
的轨迹为( )
椭圆 双曲线 抛物线 线段
16.在平面直角坐标系中,点A、点B到直线l的距离分别为1、2,则符合条件的直线l的条数为( )
、1 ; 、2 ; 、3; 、4.
3、 解答卷(共48分)
17.(8分)已知复数![]() .
.
(1)比较![]() 的大小;
的大小;
(2)判断复数![]() 在复平面上所对应的点
在复平面上所对应的点![]() 与圆
与圆![]() 的地方关系.
的地方关系.
18.(8分)已知![]()
(1)当![]() 时,求直线AB;
时,求直线AB;
(2)当 ,求直线AB的倾斜角α的取值范围.
,求直线AB的倾斜角α的取值范围.
19.(8分)已知关于![]() 的方程
的方程![]() :
:![]() ,
,![]() R表示圆.
R表示圆.
求![]() 的取值范围;
的取值范围;
若该圆与直线![]() :
:![]() 相交于
相交于![]() 两点,且
两点,且![]() =
=![]() ,求实数
,求实数![]() 的值.
的值.
20、(10分)已知点![]() 、
、![]() 依次为双曲线
依次为双曲线![]() 的左右焦点,
的左右焦点,![]() ,
,![]() ,
,![]()
(1)若![]() ,以
,以![]() 为方向向量的直线
为方向向量的直线![]() 经过
经过![]() ,求
,求![]() 到
到![]() 的距离;
的距离;
(2)若双曲线![]() 上存在点
上存在点![]() ,使得
,使得![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
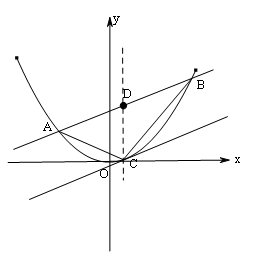
21、(14分)如图,直线![]() 与抛物线
与抛物线![]() (常数
(常数![]() )相交于不一样的两点
)相交于不一样的两点![]() 、
、![]() ,且
,且![]() (
(![]() 为定值),线段
为定值),线段![]() 的中点为
的中点为![]() ,与直线
,与直线![]() 平行的切线的切点为
平行的切线的切点为![]() (不与抛物线对称轴平行或重合且与抛物线只有一个公共点的直线称为抛物线的切线,这个公共点为切点).
(不与抛物线对称轴平行或重合且与抛物线只有一个公共点的直线称为抛物线的切线,这个公共点为切点).
用![]() 、
、![]() 表示出
表示出![]() 点、
点、![]() 点的坐标,并证明
点的坐标,并证明![]() 垂直于
垂直于![]() 轴;
轴;
(2)求![]() 的面积,证明
的面积,证明![]() 的面积与
的面积与![]() 、
、![]() 无关,只与
无关,只与![]() 有关;
有关;
(3)小明所在的兴趣小组完成上面两个小题后,小明连![]() 、
、![]() ,再作与
,再作与![]() 、
、![]() 平行的切线,切点分别为
平行的切线,切点分别为![]() 、
、![]() ,小明立刻写出了
,小明立刻写出了![]() 、
、![]() 的面积,由此小明求出了直线
的面积,由此小明求出了直线![]() 与抛物线围成的面积,你觉得小明能做到吗?请你说出理由.
与抛物线围成的面积,你觉得小明能做到吗?请你说出理由.
第一学期上大附中期末考试
高二 数学试题
1、 填空题(共36分)
1. ![]() __________
__________
2. 双曲线![]() 的渐近线方程是___
的渐近线方程是___![]() _______
_______
__________
3. 已知矩阵![]() ,则AB=__________
,则AB=__________![]() __________.
__________.
4.已知![]() ,
,![]() ,若
,若![]() ,则实数
,则实数![]() _______.-2
_______.-2
__________
5. 行列式 中,第2行第1列元素的代数余子式的值为
中,第2行第1列元素的代数余子式的值为![]() ,则实数
,则实数![]() __________;
__________;
6. 已知直线![]() :
:![]() 与
与![]() :
:![]() 平行,则k的值是__________. 3或5
平行,则k的值是__________. 3或5
7.若向量![]() 的夹角为
的夹角为![]() ,
,![]() ,则
,则![]() __________
__________
8.已知实数![]() 、
、![]() 满足条件
满足条件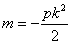 ,则
,则![]() 的最大值为__
的最大值为__![]() _______
_______
9.曲线C的方程是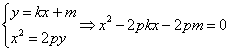 ,则曲线C被坐标轴所截的线段长d=__13
,则曲线C被坐标轴所截的线段长d=__13
10. 椭圆![]() 上一点
上一点![]() 到焦点
到焦点![]() 的距离为4,
的距离为4,![]() 为原点,
为原点,![]() 为
为![]() 的中点,则
的中点,则![]() __________
__________
11.设![]() 是曲线
是曲线![]() 上的点,
上的点,![]() ,
,![]() ,则
,则![]()
的最大值为__________
12、已知各项均为正数的数列![]() 满足
满足![]() (
(![]() ),且
),且![]() ,则首项
,则首项![]() 所大概取值中最大值为______32____________
所大概取值中最大值为______32____________
2、 选择题(每题4分,共16分)
13. 已知复数![]() (
(![]() 为虚数单位),在复平面内,
为虚数单位),在复平面内,![]() 对应的点在( B )
对应的点在( B )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
14. 在平行四边形ABCD中,下列结论中错误的是( C )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
![]()
15.已知![]() ,
,![]() ,则
,则![]() 对应的点
对应的点![]() 的轨迹为( D )
的轨迹为( D )
椭圆 双曲线 抛物线 线段
16.在平面直角坐标系中,点A、点B到直线l的距离分别为1、2,则符合条件的直线l的条数为 B
、1 ; 、2 ; 、3; 、4.
3、 解答卷(共48分)
17.(8分)已知复数![]() .
.
(1)比较![]() 的大小;
的大小;
(2)判断复数![]() 在复平面上所对应的点
在复平面上所对应的点![]() 与圆
与圆![]() 的地方关系.
的地方关系.
(1)<
(2)圆内
18.(8分)已知![]()
(1)当m=2时,求直线AB;
(2)当m∈[﹣![]() ﹣1,-1),求直线AB的倾斜角α的取值范围.
﹣1,-1),求直线AB的倾斜角α的取值范围.
(1)![]()
(2)![]()
19.(8分)已知关于![]() 的方程
的方程![]() :
:![]() ,
,![]() R表示圆.
R表示圆.
求![]() 的取值范围;
的取值范围;
若该圆与直线![]() :
:![]() 相交于
相交于![]() 两点,且
两点,且![]() =
=![]() ,求实数
,求实数![]() 的值.
的值.
m<5(4分)
(2)m=1(6分)
20、(10分)已知点![]() 、
、![]() 依次为双曲线
依次为双曲线![]() 的左右焦点,
的左右焦点,![]() ,
,![]() ,
,![]()
(1)若![]() ,以
,以![]() 为方向向量的直线
为方向向量的直线![]() 经过
经过![]() ,求
,求![]() 到
到![]() 的距离;
的距离;
(2)若双曲线![]() 上存在点
上存在点![]() ,使得
,使得![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
解:![]() 的方程是:
的方程是:![]() ...................2分
...................2分
点![]() 到
到![]() 的距离为
的距离为![]() .....................2分
.....................2分
设![]() ,则
,则![]() 代入
代入![]() 得
得
![]() ①.....................2分
①.....................2分
![]() 在双曲线
在双曲线![]() 上
上 ![]() ②
②
① ,② 可得 ![]() 即
即![]()
即![]() ....................................3分
....................................3分
又![]()
![]() ..............................................1分
..............................................1分
21、(14分)如图,直线![]() 与抛物线
与抛物线![]() (常数
(常数![]() )相交于不一样的两点
)相交于不一样的两点![]() 、
、![]() ,且
,且![]() (
(![]() 为定值),线段
为定值),线段![]() 的中点为
的中点为![]() ,与直线
,与直线![]() 平行的切线的切点为
平行的切线的切点为![]() (不与抛物线对称轴平行或重合且与抛物线只有一个公共点的直线称为抛物线的切线,这个公共点为切点).
(不与抛物线对称轴平行或重合且与抛物线只有一个公共点的直线称为抛物线的切线,这个公共点为切点).
用![]() 、
、![]() 表示出
表示出![]() 点、
点、![]() 点的坐标,并证明
点的坐标,并证明![]() 垂直于
垂直于![]() 轴;
轴;
(2)求![]() 的面积,证明
的面积,证明![]() 的面积与
的面积与![]() 、
、![]() 无关,只与
无关,只与![]() 有关;
有关;
(3)小明所在的兴趣小组完成上面两个小题后,小明连![]() 、
、![]() ,再作与
,再作与![]() 、
、![]() 平行的切线,切点分别为
平行的切线,切点分别为![]() 、
、![]() ,小明立刻写出了
,小明立刻写出了![]() 、
、![]() 的面积,由此小明求出了直线
的面积,由此小明求出了直线![]() 与抛物线围成的面积,你觉得小明能做到吗?请你说出理由.
与抛物线围成的面积,你觉得小明能做到吗?请你说出理由.

21. 解:(1)由 ,得
,得![]() ,
,![]()
点![]() ,设切线方程为
,设切线方程为![]() ,由
,由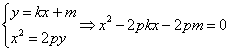 ,得
,得![]() ,
,![]() ,切点的横坐标为
,切点的横坐标为![]() ,得
,得![]()
因为![]() 、
、![]() 的横坐标相同,
的横坐标相同,![]()
![]() 垂直于
垂直于![]() 轴.
轴.
(2)![]()
![]() ,
,![]()
![]() .
.
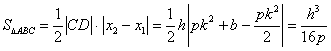 .
.
![]() 的面积与
的面积与![]() 、
、![]() 无关,只与
无关,只与![]() 有关.
有关.
(本小题也可以求![]() ,切点到直线
,切点到直线![]() 的距离
的距离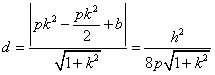 ,相应给分)
,相应给分)
(3)由(1)知![]() 垂直于
垂直于![]() 轴,
轴,![]() ,由(2)可得
,由(2)可得![]() 、
、![]() 的面积只与
的面积只与![]() 有关,将
有关,将![]() 中的
中的![]() 换成
换成![]() ,可得
,可得![]() .
.
记![]() ,
,![]() ,按上面架构三角形的办法,无限的进行下去,可以将抛物线
,按上面架构三角形的办法,无限的进行下去,可以将抛物线![]() 与线段
与线段![]() 所围成的封闭图形的面积,看成无穷多个三角形的面积的和,即数列
所围成的封闭图形的面积,看成无穷多个三角形的面积的和,即数列![]() 的无穷项和,此数列公比为
的无穷项和,此数列公比为![]() .
.
所以封闭图形的面积







