第19章 几何证明
§19.2证明举例（1）
解答卷
已知：如图，在△ABC中，AB=AC，AE是外角ÐCAD的平分线。求证：AE∥BC.
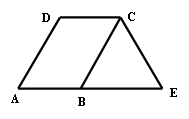
2、已知：如图，ÐA=ÐE，点E在AB的延长线上，且CE=CB。求证：AD∥BC.
3、已知：如图，AC=BD，Ð1=Ð2。求证：AD∥BC。
第19章 几何证明
§19.2证明举例（2）
1、已知：如图，在△ABC中，∠A:∠B:∠C =3:4:5，BD、CE分别是边AC、AB上的高，BD、CE相交于H. 求∠BHC的度数.
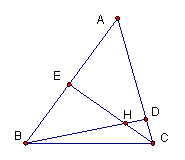
2、已知：如图所示△ABC，BE，CD相交于O，AB=AC,AD=AE，（1）求证：OD=OE，（2）联结DE，求证：DE//BC.
3、如图, AB=AC, E是AD上的一点,∠BAE=∠CAE. 求证:∠EBD=∠ECD.
第19章 几何证明
§19.2证明举例（3）
解答卷
1、已知：如图，AB=DE，BC=DF，AF=CE。求证：BC∥DF。
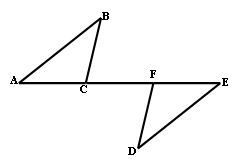
2、已知：如图，AB=DE，ÐA=ÐD，AC=DF。求证：AC∥DF.
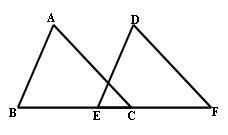
3、已知：如图，点D在AB上，E在AC上，BE和CD相交于点O，AB=AC，ÐB=ÐC，求证：BD=CE。
第19章 几何证明
§19.2证明举例（4）
1、选择题
1、下列给出的三条线段中，不可以构成直角三角形的是（ ）
A．4、8、
B.4、8、
C.7、24、25 D.7、14、15
2、设D为等腰△ABC底边BC上一点，DE∥AB,DF∥AC,则四边形AFDE的周长是（ ）
A、2AB B、2AB+BC C、2BC D、AB+BC
3、如图，△ABC中边AB的垂直平分线分别交BC、AB于点D、E，AE=3cm，△ADC的周长为9cm，则△ABC的周长是（ ）
A、12cm B、15cm
C、21cm D、18cm
2、填空题
4、假如周长为20的长方形一边为
，那样它的面积
关于的函数分析式是_________________
5、在Rt△ABC中，若∠C=90°，D是BC边上一点，且AD=2CD,则∠ADB=______________°
6、在Rt△ABC中，∠C=90°，∠A的平分线交BC于点D，且BC=8，BD=5，那样点D到AB的距离是____________
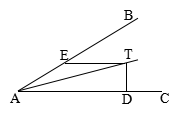
3、简答卷
7、如图：已知 
BAC=30°，AT平分BAC，TE∥AC.
（1）求证：AET是等腰三角形；
（2）若TD
AC ，垂足为点D，AE=4cm，求TD的长.
第19章 几何证明
§19.2证明举例（1）
1.证明：
由于ÐCAD是△ABC的外角
所以ÐCAD=∠B+∠C
由于AB=AC
所以∠B=∠C
所以∠CAD=2∠B
由于AE是ÐCAD的平分线
所以∠CAD=2∠DAE
所以∠B=∠DAE
所以AE∥BC.
2.证明：
由于CE=CB
所以∠CBE=∠E
由于ÐA=ÐE
所以∠CBE=∠A
所以AD∥BC
3.证明：
由于Ð1=Ð2
所以OB=OC
由于AC=BD
所以OA=OD
所以∠OAD=∠ODA
由于Ð1+Ð2+∠BOC=180°
∠OAD+∠ODA+∠AOD=180°
∠BOC=∠AOD
所以Ð1+Ð2=∠OAD+∠ODA
所以2Ð1=2∠ODA
即Ð1=∠ODA
所以AD∥BC
第19章 几何证明
§19.2证明举例（2）
1.答案：
135°
分析：
由于∠A+∠B+∠C =180°
由于∠A:∠B:∠C =3:4:5
所以∠A=45°
由于BD、CE分别是边AC、AB上的高
所以∠BEH=90°，∠ADB=90°
在△ABC中∠A+∠ADB+∠ABD=180°
所以∠ABD=45°
由于∠BHC=∠ABD+∠BEH
所以∠BHC=90°+45°=135°
2.证明：在△ADC和△AEB中
AB=AC；
∠A=∠A；
AD=AE，
所以△ADC≌△AEB
所以∠ABE=∠ACD,AE=AD
由于AB=AC
所以BD=EC
在△BDO和△CEO中
BD=EC
∠ABE=∠ACD
∠DOB=∠EOC
所以△BDO≌△CEO
所以OD=OE
3.证明：在△ABD和△ACD中
AB=AC；
∠BAE=∠CAE;
AD=AD，
所以△ABD≌△ACD
所以∠ADB=∠ADC,BD=CD
在△BDE和△CDE中
DB=DB
∠ADB=∠ADC,
BD=CD
所以△BDE≌△CDE
所以∠EBD=∠ECD
第19章 几何证明
§19.2证明举例（3）
1.证明：
由于AF=CE
所以AC=EF
在△ABC和△DEF中
AC=EF；
AB=DE;
BC=DF，
所以△ABC≌△DEF
所以∠ACB=∠EFD,
所以∠BCF=∠DFC,
所以BC∥DF
2.证明：
在△ABC和△DEF中
AB=DE；
ÐA=ÐD ;
AC=DF，
所以△ABC≌△DEF
所以∠ACB=∠DFE,
所以AC∥DF
3..证明：
在△ABE和△ACD中
ÐB=ÐC;
AB=AC；
ÐA=ÐA，
所以△ABE≌△ACD
所以AD=AE
由于AB=AC
所以BD=CE
第19章 几何证明
§19.2证明举例（4）
1.答案：D
分析：依据直角三角形的逆命题，可知7与14的平方和不等于15的平方，故选D
2.答案：A
分析：由DE∥AB,DF∥AC，可得四边形AFDE是平行四边形，再可得BF=DF,DE=EC，所以四边形AFDE的周长是2AB，故选A
3.答案：B
分析：由E是边AB的垂直平分线，可得AD=BD,AE=BE, 由△ADC的周长为9cm，可得AC+BC=9，AB=6,所以△ABC的周长是15cm,故选B
4.答案：y=x
分析：由周长为20的长方形一边为，可知长方形另一边为10-x,那样它的面积是x
故y=x
5.答案：
120°
分析：在Rt△ABD中AD=2CD可知∠CAD=30°，∠ADB=90°+30°=120°
6.答案：3
分析：依据角平分线定理可得到AB的距离等于CD的长，由BC=8，BD=5可得CD=3
7.答案：（1）见分析
（2）2 cm
分析：
（1）由AT平分BAC，TE∥AC.可得AET是等腰三角形
（2）过点T作TFAB，垂足点F，依据角平分线定理可得DT=TF
在RT△TFE中，ET=4cm，∠FET=30°，则TF=2cm,则TD=2cm
