初三(上)月考数学试题
一.选择题(共6小题)
1.已知线段a=3,c=12,则线段a和c的比率中项b是()
A.±6 B.36 C.6 D.﹣6
2.已知:在一张比率尺为1:20000的地图上,量得A、B两地的距离是5cm,那样A、B两地的实质距离是()
A.500m B.1000m C.5000m D.10000m
3.在下列条件中,不可以判断△ABC与△DEF一样的是()
A.∠A=∠D,∠B=∠E B.![]() =
=![]() 且∠B=∠E
且∠B=∠E
C.![]() =
=![]() =
=![]() D.
D.![]() =
=![]() 且∠A=∠D
且∠A=∠D
4.将二次函数y=x2的图象沿y轴方向向上平移1个单位,则所得到图象的函数分析式为()
A.y=x2+1 B.y=x2﹣1 C.y=(x+1)2 D.y=(x﹣1)2
5.假如二次函数y=ax2+bx﹣c的图象如图所示,那样下列判断正确的是()
A.a>0,c>0,b>0 B.a<0,c<0,b>0
C.a>0,c<0,b<0 D.a<0,c<0,b<0
6.下列四个三角形中,与图中△ABC的一样的是()
A. B.
B.
C. D.
D.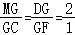
二.填空题(共12小题)
7.假如两个相似三角形对应的高之比是2:3,那样它们对应的角平分线之比是__________.
8.如图,在△ABC中,DE∥BC,AD=8cm,AE=6cm,CE=3cm,那样DB=__________cm.
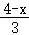
9.如图AB∥CD,AD与BC相交于点E,假如AB=2,CD=4,BC=5,那样BE=__________.
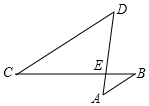
10.在△ABC中AD是中线,若G是△ABC的重点,则AG:AD的值是__________.
11.如图,在菱形ABCD中,∠ABC=60°,AE⊥AB,交BD于点G,交BC的延长线于点E,那样![]() =__________.
=__________.

12.假如二次函数y=(m﹣2)x2+3x+m2﹣4的图象经过原点,那样m=__________.
13.y=ax2+bx+c过点A(﹣1,0),B(3,0),则此抛物线的对称轴是直线x=__________.
14.已知二次函数y=kx2﹣7x﹣7的图象和x轴有交点,则k的取值范围__________.
15.已知二次函数的图象的顶点坐标是(﹣1,﹣6),并且该图象经过点(2,3)表达式为__________.
16.已知抛物线y=x2﹣(k+3)x+9的顶点在坐标轴上,则k=__________.
17.菱形ABCD边长为4,点E在直线AD上,DE=3,连接BE与对角线AC交点M,那样![]() 的值是__________.
的值是__________.
18.如图,Rt△ABC中,∠ACB=90°,AC=4,BC=5,点P为AC上一点,将△BCP沿直线BP翻折,点C落在C′处,连接AC′,若AC′∥BC,那样CP的长为__________.

三.解答卷(共7小题)
19.如图已知在直角坐标系中,一条抛物线与x轴交于A、B两点,与y轴交于C点,其中B(3,0),C(0,4),点A在x轴的负半轴上,OC=4OA:
(1)求点A坐标;
(2)求这条抛物线的分析式,并求出它的顶点坐标.
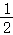
20.如图,已知DE∥BC,FE∥CD,AF=3,AD=5,AE=4.
(1)求CE的长;
(2)求AB的长.

21.如图,在梯形ABCD中,AD∥BC,∠A=90°,BD⊥CD.已知AD=3,AB=4,求S△BCD.

22.在直角坐标平面内,点O在坐标原点,已知点A(3,1)、B(2,0)、C(4,﹣2).
(1)求证:△AOB∽△OCB;
(2)求∠AOC的度数.
23.如图:已知在△ABC中,AB=AC,点D是BC上一点,∠ADE=∠B,
(1)求证:△ABD~△DCE;
(2)点F在AD上,且![]() =
=![]() ,求证:EF∥CD.
,求证:EF∥CD.
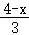
24.如图,已知在平面直角坐标系xOy中,顶点为M的抛物线C1:y=ax2+bx(a<0)经过点A和x轴上的点B,AO=OB=2,∠AOB=120°.
(1)求该抛物线的表达式;
(2)连结AM,求S△AOM;
(3)设点F是x轴上一点,假如△MBF与△AOM相似,求所有符合条件的点F的坐标.

25.如图,已知等腰梯形ABCD中,AD∥BC,AD:BC=1:2,点E为边AB中点,点F是边BC上一动点,线段CE与线段DF交于点G.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)连接AG,在(1)的条件下,写出线段AG和线段DC的地方关系和数目关系,并说明理由;
(3)连接AG,若AD=2,AB=3,且△ADG与△CDF相似,求BF的长.
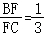
参考答案与考试试题分析
一.选择题(共6小题)
1.已知线段a=3,c=12,则线段a和c的比率中项b是()
A.±6 B.36 C.6 D.﹣6
【剖析】依据比率中项的概念可得b2=ac,从而易求b,注意线段没负值.
【解答】解:∵b是线段a、c的比率中项,
∴b2=ac,
即b2=3×12=36,
∴b=6(负数舍去),
故选:C.
2.已知:在一张比率尺为1:20000的地图上,量得A、B两地的距离是5cm,那样A、B两地的实质距离是()
A.500m B.1000m C.5000m D.10000m
【剖析】第一设A,B两地的实质距离为xcm,依据题意可得方程![]() =
=![]() ,解此方程即可求得答案.
,解此方程即可求得答案.
【解答】解:设A,B两地的实质距离为xcm,
依据题意得:![]() =
=![]() ,
,
解得:x=100000,
∵100000cm=1000m,
∴A,B两地的实质距离是1000m.
故选:B.
3.在下列条件中,不可以判断△ABC与△DEF一样的是()
A.∠A=∠D,∠B=∠E B.![]() =
=![]() 且∠B=∠E
且∠B=∠E
C.![]() =
=![]() =
=![]() D.
D.![]() =
=![]() 且∠A=∠D
且∠A=∠D
【剖析】直接依据三角形一样的断定办法分别判断得出答案.
【解答】解:A、∠A=∠D,∠B=∠E,可以得出△ABC∽△DFE,故此选项不合题意;
B、![]() =
=![]() ,且∠B=∠E,不是两边成比率且夹角相等,故此选项符合题意;
,且∠B=∠E,不是两边成比率且夹角相等,故此选项符合题意;
C、![]() =
=![]() =
=![]() ,可以得出△ABC∽△DFE,故此选项不合题意;
,可以得出△ABC∽△DFE,故此选项不合题意;
D、![]() =
=![]() 且∠A=∠D,可以得出△ABC∽△DFE,故此选项不合题意;
且∠A=∠D,可以得出△ABC∽△DFE,故此选项不合题意;
故选:B.
4.将二次函数y=x2的图象沿y轴方向向上平移1个单位,则所得到图象的函数分析式为()
A.y=x2+1 B.y=x2﹣1 C.y=(x+1)2 D.y=(x﹣1)2
【剖析】直接依据“上加下减”的原则进行解答即可.
【解答】解:由“上加下减”的原则可知:二次函数y=x2的图象沿y轴方向向上平移1个单位,则所得到图象的函数分析式为:y=x2+1.
故选:A.
5.假如二次函数y=ax2+bx﹣c的图象如图所示,那样下列判断正确的是()
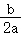
A.a>0,c>0,b>0 B.a<0,c<0,b>0
C.a>0,c<0,b<0 D.a<0,c<0,b<0
【剖析】抛物线开口方向,对称轴,与y轴交点的地方确定a、b、c的符号,从而做出判断.
【解答】解:抛物线开口向下,因此a<0,对称轴偏在y轴右边,a、b异号,因此b>0,抛物线与y轴交在正半轴,因此﹣c>0,即:c<0,
故选:B.
6.下列四个三角形中,与图中△ABC的一样的是()

A. B.
B.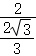
C.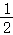 D.
D.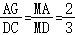
【剖析】借助相似三角形的断定办法判断即可.
【解答】解:由题意得:BC=2,AC=4,即BC:AC=1:2,且∠C=90°,
图中直角边为![]() ,2
,2![]() ,之比也为1:2,
,之比也为1:2,
则与图中△ABC的一样的是B,
故选:B.
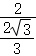
二.填空题(共12小题)
7.假如两个相似三角形对应的高之比是2:3,那样它们对应的角平分线之比是__________.
【剖析】依据相似三角形对应高线的比等于相似比,对应角平分线的比等于相似比解答即可.
【解答】解:∵相似三角形对应高线的比是2:3,
∴它们的相似比为2:3,
∴它们对应角平分线的比是2:3.
故答案为:2:3.
8.如图,在△ABC中,DE∥BC,AD=8cm,AE=6cm,CE=3cm,那样DB=__________cm.

【剖析】依据平行线分线段成比率定理进行计算即可.
【解答】解:∵DE∥BC,AD=8cm,AE=6cm,CE=3cm,
∴![]() ,即
,即![]() ,
,
∴DB=4(cm).
9.如图AB∥CD,AD与BC相交于点E,假如AB=2,CD=4,BC=5,那样BE=__________![]() __________.
__________.
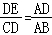
【剖析】由AB∥CD可得出△ABE∽△DCE,再借助相似三角形的性质可求出BE的长.
【解答】解:∵AB∥CD,
∴△ABE∽△DCE,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴BE=![]() .
.
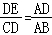
10.在△ABC中AD是中线,若G是△ABC的重点,则AG:AD的值是__________![]() __________.
__________.
【剖析】本题先判断点G为三角形的重点,然后依据三角形重心的性质来求比值,从而非常简单地解得.
【解答】解:∵G是△ABC的重点,且AD是中线,
∴AG=2GD,
∴AG:AD=2:3.
故答案为![]()
11.如图,在菱形ABCD中,∠ABC=60°,AE⊥AB,交BD于点G,交BC的延长线于点E,那样![]() =__________
=__________![]() __________.
__________.

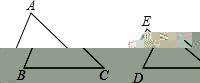
【剖析】依据菱形的性质得:AD=AB=BC,由∠ABC=60°得:AB=AD=![]() BE,最后依据△ADG∽△EBG得到比率式求出AG与GE的比值即可.
BE,最后依据△ADG∽△EBG得到比率式求出AG与GE的比值即可.
【解答】解:∵四边形ABCD为菱形,
∴AD=AB=BC,
∵AE⊥AB,∠ABC=60°,
∴AB=AD=![]() BE,
BE,
∵AD∥BE,
∴△ADG∽△EBG,
∴![]() =
=![]() =
=![]() .
.
故答案为:![]() .
.
12.假如二次函数y=(m﹣2)x2+3x+m2﹣4的图象经过原点,那样m=__________.
【剖析】将原点坐标(0,0)代入二次函数分析式,列方程求m,注意二次项系数m﹣2≠0.
【解答】解:∵点(0,0)在抛物线y=(m﹣2)x2+x+(m2﹣4)上,
∴m2﹣4=0,
解得m=±2,
又二次项系数m﹣2≠0,
∴m=﹣2.
故答案为:﹣2.
13.y=ax2+bx+c过点A(﹣1,0),B(3,0),则此抛物线的对称轴是直线x=__________.
【剖析】依据点A、B的纵坐标相等,借助二次函数的对称性列式计算即可得解.
【解答】解:∵点A(﹣1,0),B(3,0)纵坐标都是0,
∴此抛物线的对称轴是直线x=![]() =1.
=1.
故答案为:
1.
14.已知二次函数y=kx2﹣7x﹣7的图象和x轴有交点,则k的取值范围______________________________![]() ______________________________.
______________________________.
【剖析】因为二次函数与x轴有交点,故二次函数对应的一元二次方程kx2﹣7x﹣7=0中,△≥0,解不等式即可求出k的取值范围,由二次函数概念可知,k≠0.
【解答】解:∵二次函数y=kx2﹣7x﹣7的图象和x轴有交点,
∴![]() ,
,
∴k≥﹣![]() 且k≠0.
且k≠0.
故答案为k≥﹣![]() 且k≠0.
且k≠0.
15.已知二次函数的图象的顶点坐标是(﹣1,﹣6),并且该图象经过点(2,3)表达式为________________________________________________________________________________.
【剖析】依据抛物线的顶点坐标设出,抛物线的分析式为:y=a(x+1)2﹣6,再把(2,3)代入,求出a的值,即可得出二次函数的分析式.
【解答】解:设抛物线的分析式为:y=a(x+1)2﹣6,
把(2,3)代入分析式得a=1,
则抛物线的分析式为:y=(x+1)2﹣6,即y=x2+2x﹣5.
故答案为:y=x2+2x﹣5.
16.已知抛物线y=x2﹣(k+3)x+9的顶点在坐标轴上,则k=__________.
【剖析】因为抛物线的顶点在坐标轴上,故应分在x轴上与y轴上两种状况进行讨论.
【解答】解:当抛物线y=x2﹣(k+3)x+9的顶点在x轴上时,△=0,
即△=(k+3)2﹣4×9=0,解得k=3或k=﹣9;
当抛物线y=x2﹣(k+3)x+9的顶点在y轴上时,x=﹣![]() =
=![]() =0,解得k=﹣3.
=0,解得k=﹣3.
故答案为:3,﹣9,﹣3.
17.菱形ABCD边长为4,点E在直线AD上,DE=3,连接BE与对角线AC交点M,那样![]() 的值是__________
的值是__________![]() __________
__________![]() __________.
__________.
【剖析】依据菱形的性质,可得对边平行,即可得到△AME∽△CMB,注意作图时需要剖析点E在线段AD上还是在线段AD的延长线上.
【解答】解:①如图:

∵四边形ABCD是菱形,
∴AD=BC=4,AD∥BC,
∴△AME∽△CMB,
∴![]() ,
,
∵DE=3,
∴AE=AD﹣DE=1,
∴![]() ,
,
②如图:
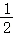
∵四边形ABCD是菱形,
∴AD=BC=4,AD∥BC,
∴△AME∽△CMB,
∴![]() ,
,
∵DE=3,
∴AE=AD+DE=7,
∴![]() ,
,
故答案为:![]() 或
或![]() .
.
18.如图,Rt△ABC中,∠ACB=90°,AC=4,BC=5,点P为AC上一点,将△BCP沿直线BP翻折,点C落在C′处,连接AC′,若AC′∥BC,那样CP的长为__________![]() __________.
__________.

【剖析】过点C'作C'D⊥BC于点D,通过题意可证四边形C'DCA是矩形,可得CD=AC',C'D=AC=4,依据勾股定理可求BD=3,即CD=AC'=2,依据勾股定理可求CP的长.
【解答】解:过点C'作C'D⊥BC于点D,

∵A'C∥BC,∠ACB=90°,
∴∠C'AC=∠ACB=90°,且C'D⊥BC,
∴四边形C'DCA是矩形,
∴CD=AC',C'D=AC=4,
∵折叠
∴BC'=BC=5,CP=C'P,
在Rt△BDC'中,BD=![]() =3
=3
∴CD=BC﹣BD=2
∴AC'=2,
在Rt△AC'P中,C'P2=C'A2+AP2,
∴CP2=4+(4﹣CP)2,
∴CP=![]()
故答案为:![]()
三.解答卷(共7小题)
19.如图已知在直角坐标系中,一条抛物线与x轴交于A、B两点,与y轴交于C点,其中B(3,0),C(0,4),点A在x轴的负半轴上,OC=4OA:
(1)求点A坐标;
(2)求这条抛物线的分析式,并求出它的顶点坐标.

【剖析】(1)依据B(3,0),C(0,4),点A在x轴的负半轴上,OC=4OA,可以求得OA的长,从而可以得到点A的坐标;
(2)依据点A和点B的坐标可以设出该抛物线的分析式,然后依据抛物线经过点C可以求得该抛物线的分析式,并求得该抛物线的顶点坐标,本题得以解决.
【解答】解:(1)∵B(3,0),C(0,4),点A在x轴的负半轴上,OC=4OA,
∴OC=4,
∴OA=1,
∴点A的坐标为(﹣1,0);
(2)设这条抛物线的分析式为y=a(x+1)(x﹣3),
∵点C(0,4)在此抛物线上,
∴4=a(0+1)(0﹣3),
解得,a=﹣![]() ,
,
∴y=﹣![]() (x+1)(x﹣3)=
(x+1)(x﹣3)=![]() +4=﹣
+4=﹣![]() +
+![]() ,
,
∴该抛物线的顶点坐标为(1,![]() ),
),
即这条抛物线的分析式为y=![]() +4,它的顶点坐标是(1,
+4,它的顶点坐标是(1,![]() ).
).
20.如图,已知DE∥BC,FE∥CD,AF=3,AD=5,AE=4.
(1)求CE的长;
(2)求AB的长.
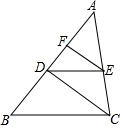
【剖析】依据平行线分线段成比率定理列出比率式,代入计算即可.
【解答】解:(1)∵FE∥CD,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得,AC=![]() ,
,
则CE=AC﹣AE=![]() ﹣4=
﹣4=![]() ;
;
(2)∵DE∥BC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得,AB=![]() .
.
21.如图,在梯形ABCD中,AD∥BC,∠A=90°,BD⊥CD.已知AD=3,AB=4,求S△BCD.

【剖析】在Rt△ABD中,借助勾股定理求出BD的长,再依据两直线平行,内错角相等可得∠ADB=∠DBC,然后证明△ABD与△DCB相似,依据相似三角形对应边成比率求出CD的长,然后再借助三角形的面积公式进行求解.
【解答】解:在Rt△ABD中,
∵∠A=90°,AD=3,AB=4,
∴BD=![]() =
=![]() =5,
=5,
又∵AD∥BC,
∴∠ADB=∠DBC,
∵∠BDC=∠A=90°,
∴△ABD∽△DCB,
∴![]() =
=![]() ,
,
即![]() =
=![]() ,
,
解得CD=![]() ,
,
∴S△BCD=![]() ×BD×CD=
×BD×CD=![]() ×5×
×5×![]() =
=![]() .
.
(注:借助相似三角形面积的比等于相似比的平方求解也可,参照给分)
22.在直角坐标平面内,点O在坐标原点,已知点A(3,1)、B(2,0)、C(4,﹣2).
(1)求证:△AOB∽△OCB;
(2)求∠AOC的度数.
【剖析】(1)分别求AB,OB,BC的长即可求得![]() =
=![]() ,即可断定;
,即可断定;
(2)依据相似三角形对应角相等即可解题.
【解答】解:如图:

(1)∵A(3,1)、B(2,0)、C(4,﹣2).
∴AB=![]() ,BC=
,BC=![]() ,OB=2,
,OB=2,
![]() =
=![]() ,
,
∵∠ABx=∠CBx=45°,
∴∠ABO=∠CBO=135°,
∴△AOB∽△OCB.
(2)∵△AOB∽△OCB.
∴∠BOC=∠A,
∵∠AOC=∠AOB+∠BOC=∠AOB+∠A,
∴∠AOC=45°.
23.如图:已知在△ABC中,AB=AC,点D是BC上一点,∠ADE=∠B,
(1)求证:△ABD~△DCE;
(2)点F在AD上,且![]() =
=![]() ,求证:EF∥CD.
,求证:EF∥CD.

【剖析】(1)由等腰三角形的性质可得∠B=∠C,由三角形的外角性质可得∠EDC=∠BAD,可得结论;
(2)由相似三角形的性质可得![]() ,可得
,可得![]() ,可证△AEF∽△ACD,可得∠AEF=∠ACD,可证EF∥CD.
,可证△AEF∽△ACD,可得∠AEF=∠ACD,可证EF∥CD.
【解答】证明;(1)∵AB=AC,
∴∠B=∠C,
∵∠ADC=∠B+∠BAD=∠ADE+∠CDE,且∠ADE=∠B,
∴∠EDC=∠BAD,且∠B=∠C,
∴△ABD~△DCE;
(2)∵△ABD~△DCE,
∴![]() ,且
,且![]() =
=![]() ,
,
∴![]()
∴![]() ,且∠EAF=∠DAC,
,且∠EAF=∠DAC,
∴△AEF∽△ACD,
∴∠AEF=∠ACD,
∴EF∥CD.
24.如图,已知在平面直角坐标系xOy中,顶点为M的抛物线C1:y=ax2+bx(a<0)经过点A和x轴上的点B,AO=OB=2,∠AOB=120°.
(1)求该抛物线的表达式;
(2)连结AM,求S△AOM;
(3)设点F是x轴上一点,假如△MBF与△AOM相似,求所有符合条件的点F的坐标.

【剖析】(1)过点A作AN⊥x轴于点N,∠AOB=120°,则∠AON=60°,ON=![]() OA=1,AN=
OA=1,AN=![]() ,故点A(﹣1,﹣
,故点A(﹣1,﹣![]() ),即可求解;
),即可求解;
(2)S△AOM=![]() ×OH(xM﹣xA)=
×OH(xM﹣xA)=![]() ×2=
×2=![]() ;
;
(3)分∠BMF为钝角、∠MBF为钝角两种状况,分别求解即可.
【解答】解:(1)过点A作AN⊥x轴于点N,
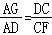
∵∠AOB=120°,则∠AON=60°,ON=![]() OA=1,AN=
OA=1,AN=![]() ,
,
故点A(﹣1,﹣![]() ),
),
将点A、B(2,0)的坐标代入抛物线表达式得:![]() ,解得:
,解得: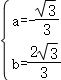 ,
,
故抛物线的表达式为:y=﹣![]() x2+
x2+![]() ;
;
(2)如上图,连接AM交x轴于点H,
将点A、M(1,![]() )的坐标代入一次函数的表达式并解得:
)的坐标代入一次函数的表达式并解得:
直线AM的表达式为:y=![]() x﹣
x﹣![]() ,故OH=
,故OH=![]() ,
,
S△AOM=![]() ×OH(xM﹣xA)=
×OH(xM﹣xA)=![]() ×2=
×2=![]() ;
;
(3)由点的坐标知:OA=2,OM=![]() ,AM=
,AM=![]() ,MB=
,MB=![]() ,
,
①当∠BMF为钝角时,
当△OAM∽△MBF时,则![]() ,
,
即:![]() =
=![]() ,解得:BF=
,解得:BF=![]() ;
;
当△OAM∽△MFB时,
同理可得:BF=![]() ,
,
故点F的坐标为:(![]() ,0)或(
,0)或(![]() ,0);
,0);
∵∠MBO=30°,
当∠BMF=150°时,∠BFM=0°,三角形没有了,故点F舍去;
②当∠MBF为钝角时,
同理可得:点F的坐标为:(4,0)或(![]() ,0);
,0);
综上,点F的坐标为:(4,0)或(![]() ,0).
,0).
25.如图,已知等腰梯形ABCD中,AD∥BC,AD:BC=1:2,点E为边AB中点,点F是边BC上一动点,线段CE与线段DF交于点G.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)连接AG,在(1)的条件下,写出线段AG和线段DC的地方关系和数目关系,并说明理由;
(3)连接AG,若AD=2,AB=3,且△ADG与△CDF相似,求BF的长.

【剖析】(1)延长CE和DA,相交于M,依据平行线分线段成比率进行计算可以求出![]() 的值.(2)依据对应线段的比相等可以得到AG与DC的地方和数目关系.(3)依据两三角形相似,对应线段的比相等,求出线段BF的长.
的值.(2)依据对应线段的比相等可以得到AG与DC的地方和数目关系.(3)依据两三角形相似,对应线段的比相等,求出线段BF的长.
【解答】解:(1)∵BF:FC=1:3,∴设BF=k,
则FC=3k,BC=4k,∵AD:BC=1:2,∴AD=2k,
如图:延长CE交DA的延长线于点M,
∵AD∥BC,
∴![]() ,且
,且![]()
∵点E为边AB中点,
∴AM=BC=4k,
∴DM=DA+AM=2k+4k=6k,
∴![]() .
.
(2)AG∥DC,且![]() .
.
证明:∵AD∥BC,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴AG∥DC.
∴![]() .
.
(3)∵ABCD是等腰梯形,AD=2,AD:BC=1:2,
∴BC=4,
∵AD∥BC,
∴∠ADG=∠DFC,
∵△ADG∽△CDF,
∴∠AGD=∠FDC或∠DAG=∠FDC.
状况1,当∠AGD=∠FDC时,有AG∥DC,延长CE交DA的延长线于点M,可得AM=4,
由![]() 得
得![]() ,
,
∴AG=2
∵△ADG与△CDF相似,且∠AGD=∠FDC,
∴![]() ,即
,即![]() ,
,
∴CF=3
∴BF=1.
状况2,当∠DAG=∠FDC时,延长AG交BC于点T,可得△ABT∽△FCD,
则![]() ,由AD∥BC得
,由AD∥BC得![]() ,
,
设BF=x,可得FT=![]() ,
,
∴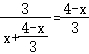 ,
,
整理得:2x2﹣4x+11=0,
∵△=16﹣88<0,
∴无实数根;
∴BF=1.








