2019-2020学年鞍山实验学校初三第一学期数学首次月考考试试题
选择题：（本大题共6题，每题3分，满分18分）
已知两个相似三角形的周长比为4：9，则它们的面积比为（ ）
A.4：9 B.2：3 C.8：
18 D.16：81
已知△ABC中，D，E分别是BC，AC上的点，下列各式中，不可以判断DE//AB的是（ ）
A.
=
B.
=
C.
=
D.
=
如图，已知向量
、
、
，那样下列结论正确的是（ ）
A.+= B.
+= C.+= D.+=-
第3题 第4题
已知P为线段AB的黄金分割点，且AP
A.=AB·PB; B.
= AP·PB; C.
= AP·AB; D.
+ 
=
.
P是△ABC一边上的一点（P不与A,B,C重合），过点P的一条直线截△ABC，假如截得的三角形与△ABC相似，大家称这条直线为过点P的△ABC的“相似线”.RT△ABC中，∠C=90
，∠A=30，当点P为AC的中点时，过点P的△ABC的“相似线”最多有几条？（ ）
A.1条 B.2条 C. 3条 D.4条
如图，在RT△ABC中，∠C=90 ,CD⊥AB，D为垂足，且BC：AC=2：3，那样BD：AD=（ ）
A.2:3 B.4:9 C.2:5 D. 
:
填空题：（本大题共12题，每题3分，满分36分）
已知，那样
=，那样
=_____.
在比率尺为1：
10000000的地图上，上海与香港之间的距离为12.3厘米，则上海与香港之间的实质距离为_____千米。
已知线段a=2cm、b=8cm，那样线段a、b的比率中项等于_____cm
10.计算：2+3=_____.
11.点G是△ABC的重点，假如AB=AC=13,BC=10,那样AG的长是_____.
12.在△ABC中，已知点D、E分别在边AB、AC上，DE//BC.假如AD=1cm，AB=3cm，DE=4cm，那样BC=_____cm.
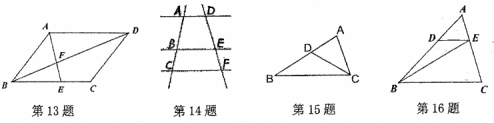
13.如图，平行四边形ABCD中，E是边BC上的点，AE交BD于点F，假如
=
，那样=_____.
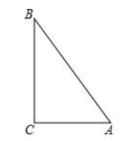
14.如图，直线AD//BE//CF，BC=AB，DE=6,那样EF的值是_____.
15.如图，在△ABC中点D在AB上，请再添一个适合的条件，使△ADC∽△ACB，那样可添加的条件是__________.
16.如图，已知点D、E分不要再△ABC边AB、AC上，DE//BC，BD=2AD,那样
:
=__________.
17.在梯形ABCD中，AD//BC，对角线AC、BD相较于点O，已知三角形ADO的面积为2，△DOC的面积为4，那样AD：BC=__________.
18.新概念：到三角形的两个顶点距离相等的点，叫做此三角形的准外心。依据准外心的概念，探究如下问题：如图，在RT△ABC中，∠C=90°,AB=10,AC=6，假如准外心P在BC边上，那样PC的长为__________。
简答卷：（本大题共4题，每题5分，满分20分）
19.如图，已知平行四边形ABCD，点M、N是边DC、BC的中点，设
=，
=
.
求向量
在图中求向量在、方向上的分向量。（不需要写作法，但要指出所作图中表示结论的向量）
20.如图，已知AB//EF//CD,AD与BC相交于点O。
假如CE=3，EB=9，DF=2，求AD的长；
假如BO：OE：EC=2：4：3，求CD的长。
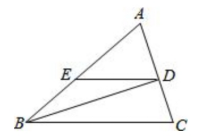21.如图，在三角形ABC中，BD是三角形ABC的角平分线，点E在边AB上，且DE//BC，已知AB=6，BC=4，求DE的长。
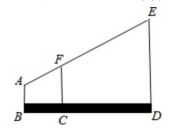
22.如图，某测量职员的双眼A与标杆顶端F、电视塔顶端E在同一条直线上，已知此人的双眼到地面的距离AB=1.6m，标杆FC=2.2m，且BC=1m，CD=5m，标杆FC、ED垂直于地面。求电视塔的高ED.
解答卷（本大题共2题，每题7分，总分14分）
23.如图，三角形ABC中，AD⊥BC于D，FGHI为矩形，=，BC=36cm，AD=12cm，求矩形FGHI的周长。
24.已知：如图，在三角形ABC中，点D、E分别在边AB、AC上，且∠ABE=∠ACD，BE、CD交于点G.
求证：△ABD∽△ABC
假如BE平分∠ABC，求证：DE=CE.
5、综合题：（本大题共1题，满分12分）
25.有一张矩形纸片ABCD，已知AB=2,AD=5.把这张纸片折叠，使点A落在边BC上的点E处，折痕为MN，MN交AB于M，交AD于N.
（1）若BE=，试着画出折痕MN的地方，并求这个时候AM的长；
（2）点E在BC上运动时，设BE=x，AN=y，试着求y关于x的函数分析式，并写出x的取值范围；
（3）连接DE，是不是存在这种点E，使得△AME与△DNE相似？若存在，请求出这个时候BE的长；若没有，请说明理由。
（备用图）
