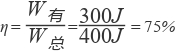专题2.6 机械效率
1.与杠杆有关的计算题解题方案
a.用杠杆提高物体的模型图
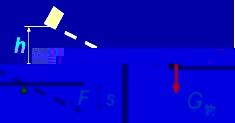
b.灵活运用杠杆平衡条件公式及其变形公式
（1）杠杆平衡条件公式公式F1L1＝F2L2
（2）求解动力，用变形公式F1＝F2L2/ L1
（3）求解动力臂，用变形公式L1＝F2L2/ F1
（4）学会杠杆平衡条件公式中每个字母代表的物理量
F1代表杠杆平衡时，遭到的动力；
L1代表杠杆平衡时的动力臂；
F2代表杠杆平衡时，遭到的阻力；
L2代表杠杆平衡时的阻力臂。
F1L1＝F2L2
这个公式表示，杠杆平衡时，动力乘以动力臂等于阻力乘以阻力臂。
c. 用杠杆提高物体有用功、额外功和总功求法
（1）用杠杆提高物体做的有用功W有用=Gh
（2）用杠杆提高物体做的总功W总= Fs
（3）用杠杆提高物体做的额外功W额外=W总—W有用
其中h是重物G被提高的高度，s是动力F 移动的距离。h与s的关系可以参考相似三角形打造。
d. 杠杆机械效率的求解
（1）用杠杆提高物体时，有用功和总功的比值.称为杠杆机械效率。
（2）杠杆机械效率公式：η＝（W有用/W总）×100％
2.与滑轮组有关的计算题解题方案
（一）用滑轮组竖直提高物体机械效率问题求解方法
a.用滑轮组竖直提高物体的模型图
b. 用滑轮组竖直提高物体有用功、额外功和总功求法
（1）有用功W有用=Gh
（2）总功W总=Fs
（3）额外功W额外=W总—W有用
（4） s=nh
其中h是重物G被提高的高度，s是动力F 移动的距离， n是动滑轮上的绳子段数。
c. 滑轮组机械效率的求解
（1）用滑轮组提高物体时，有用功和总功的比值.称为滑轮组机械效率。
（2）滑轮组机械效率公式：η＝（W有用/W总）×100％
η＝（W有用/W总）×100％= ×100％
（二）用滑轮组水平拉动物体机械效率问题求解方法
a.用滑轮组水平拉动物体的模型图
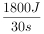
b. 用滑轮组水平拉动物体有用功、额外功和总功求法
（1）有用功W有用= fs2
（2）总功W总= F s1
（3）额外功W额外=W总—W有用
（4）s1= ns2
其中 s1是动力F 移动的距离，s2是重物水平移动的距离，f是物体匀速运动遭到的阻力， n是动滑轮上的绳子段数。
c. 滑轮组机械效率的求解
（1）用滑轮组水平拉动物体时，有用功和总功的比值.称为滑轮组机械效率。
（2）滑轮组机械效率公式：η＝（W有用/W总）×100％
η＝（W有用/W总）×100％= ×100％
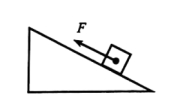
3.与斜面有关的计算题解题方案
a.用斜面提高物体的模型图
b. 用斜面提高物体有用功、额外功和总功求法
（1）有用功W有用= Gh
（2）总功W总= F s
（3）额外功W额外=W总—W有用
其中 s是动力F 沿着斜面移动的距离，h 是重物上升的高度，s和h的关系，一般可由解三角函数得到，一般斜面倾斜角给出。
c. 斜面机械效率的求解
（1）用斜面提高物体时，有用功和总功的比值.称为斜面的机械效率。
（2）斜面机械效率公式：η＝（W有用/W总）×100％
η＝（W有用/W总）×100％= ×100％
种类1.与杠杆有关的计算题
【例题1】（2019山西）汽车超载是目前发生交通事故的主要原因之一。全国各地设置了很多超载监测站加大监管。如图所示，一辆两轴货车正在水平地面上设置的某种电子地磅秤上称重。先让货车前轮单独开上电子地磅秤，其读数为8t；前轮驶离电子地磅秤，再让后轮单独开上电子地磅秤，其读数为9t。国家规定两轴货车限载车货总重18t，请你通过计算剖析该货车是不是超载。
【答案】该货车不超载。
【分析】分别以汽车前轮和后轮为支点打造杠杆模型，依据杠杆的平衡条件得出等式，联立等式即可求出车遭到的重力，然后与汽车的自己和载重相比较即可得出答案。
以汽车前轮为支点打造杠杆模型，示意图如图甲，
依据杠杆平衡条件得：F后L＝GL1﹣﹣﹣﹣①
以汽车后轮为支点打造杠杆模型，示意图如图乙，
依据杠杆平衡条件得：F前L＝GL2﹣﹣﹣﹣②
由①②两式可得：
G＝F前+F后＝（8×103kg+9×103kg）×10N/kg＜18×103kg×10N/kg，
所以，该货车不超载。
种类2.与滑轮组有关的计算题
【例题2】（2018辽宁鞍山）如图所示，借助滑轮组在2s内将重400N的物体匀速提高了1m，所用拉力F为150N．不计绳重和摩擦下列说法正确的是（）
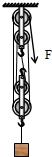
A．绳子自由端移动的速度为2m/s B．动滑轮的总重为100N
C．滑轮组的机械效率为83.3% D．提高更重的物体，滑轮组的机械效率会变小
【答案】A
【分析】本题考查了用滑轮组时动滑轮重力、绳子自由端移动速度、有用功、总功和机械效率的计算，还考查了物体重力对机械效率的影响，依据题图确定n的大小是本题的突破口。
（1）由图知，n＝4，绳子自由端移动距离s＝4h，借助速度公式求绳子自由端移动速度；（2）不计绳重及摩擦，拉力F＝（G+G动），据此求动滑轮所受的重力；
（3）借助W＝Fs求拉力做的总功，借助W＝Gh求有用功，滑轮组的机械效率等于有用功与总功之比；（4）增大滑轮组机械效率的办法：一是增大提高的物重，二是减小摩擦、减小动滑轮重。
A、由图知，n＝4，绳子自由端移动的距离：s＝4h＝4×1m＝4m，
绳子自由端移动的速度：v＝
＝
＝2m/s，故A正确；
B、不计绳重及摩擦，拉力F＝（G+G动），可得动滑轮所受的重力：
G动＝4F﹣G＝4×150N﹣400N＝200N，故B错误；
C、拉力做的功：W总＝Fs＝150N×4m＝600J，
有用功：W有用＝Gh＝400N×1m＝400J，
滑轮组的机械效率：
η＝
＝
×100%≈66.7%，故C错误；
D、若用该滑轮组提高所受重力更重的物体，额外功不变，有用功增加，有用功在总功中所占的比率增加，机械效率会变大，故D错误。
种类3.与斜面有关的计算题
【例题3】（2019甘肃兰州）如图所示，斜面长2m、高1m，把一个水平为24kg的物体沿斜面从斜面底端匀速拉到顶端，需要克服重力做功__________J。若斜面是光滑的，则沿斜面向上的拉力__________N。在“核桃钳、红酒开瓶器和家里升降晾衣架上的滑轮”三种工具中是斜面的是__________。（g=10N/kg）
【答案】240；120；红酒开瓶器。
【解答】物体的重力：G=mg=24kg×10N/kg=240N，用斜面时做的有用功：
W有=Gh=240N×1m=240J；若斜面是光滑的，则拉力所做的做等于克服物体重力所做的功，由W=Fs可得拉力：
F=120N；
“核桃钳、红酒开瓶器和家里升降晾衣架上的滑轮”这三种机械中，核桃钳是杠杆，衣架上的滑轮是滑轮组，红酒开瓶器是斜面。
1、填空题
1.（2019湖南怀化）如图所示，用滑轮组将重为100 N的物体匀速提高3m，拉力F所做的总功为400 J，则在这个过程中拉力F做了____________________J的有用功，该滑轮组的机械效率是______________________________。
【答案】300；75%。
【分析】（1）拉力做的有用功：W有用=Gh=100N×3m=300J
（2）W总=400J，滑轮组的机械效率：η=W有用/W总=300J/400J×100%=75%
2．（2019湖南娄底）既能够省力，又可以改变用力方向的滑轮是____（选填“定滑轮”“动滑轮”或“滑轮组”）；借助一个效率为90%的杠杆做100J的总功，其中额外功是____J。
【答案】滑轮组；10。
【分析】（1）用定滑轮不可以省力，但可以改变力的方向；用动滑轮可以省力，但不能改变力的方向；用定滑轮和动滑轮组成滑轮组，既能够省力，又可以改变力的方向；
（2）由题知，用杠杆做的总功W总=100J，η=90%，
可得做的有用功：W有用=W总×90%=100J×90%=90J，
则借助杠杆做的额外功：
W额=W总-W有用=100J-90J=10J。
3．（2018•威海）如图为吊装工具示意图，物体M为重5000N的配重，杠杆AB的支点为O，OA：OB=1：2，每一个滑轮重100N．当重为700N的工人用300N的力竖直向下匀速拉动绳子时，工人对地面的重压为__________N，物体M对地面的重压为__________N．（杠杆与绳的自重、滑轮组摩擦均不计）
【答案】400；4500。
【分析】（1）人受竖直向下的重力G、竖直向上的拉力F、竖直向上的支持力F支，
由力的平衡条件可得：F+F支=G，
则F支=G﹣F=700N﹣300N=400N，
由于地面对人的支持力和人对地面的重压是一对相互用途力，大小相等，
所以工人对地面的重压：F压=F支=400N；
（2）定滑轮受向下的重力、3段绳子向下的拉力、杠杆对定滑轮向上的拉力，
由力的平衡条件可得：FA′=3F+G定=3×300N+100N=1000N；
杠杆对定滑轮的拉力和定滑轮对杠杆的拉力是一对相互用途力，大小相等，即FA=F′A=1000N；
依据杠杆的平衡条件：FA×OA=FB×OB，且OA：OB=1：2，
所以：FB=
=
=500N；
由于物体间力有哪些用途是相互的，
所以杠杆对物体M的拉力等于物体M对杠杆的拉力，即FB′=FB=500N；
物体M受竖直向下的重力、竖直向上的支持力、竖直向上的拉力，
则物体M遭到的支持力为：FM支持=GM﹣FB′=5000N﹣500N=4500N，
由于物体间力有哪些用途是相互的，
所以物体M对地面的重压：FM压=FM支持=4500N。
4.（2019四川乐山）在斜面上将一个重600N的物体匀速拉到高处，沿斜面向上的拉力F=400N，拉动的距离s=4.5m，提高高度h=1.8m，所用时间t=30s。则拉力F做功的功率为______W，此过程中物体遭到的摩擦力为______N。
【答案】60 160
【分析】（1）拉力所做的总功：
W总=Fs=400N×4.5m=1800J，
拉力F做功的功率：
P=
==60W；
（2）有用功：
W有=Gh=600N×1.8m=1080J，
克服摩擦力做的额外功：
W额=W总-W有=1800J-1080J=720J，
由W额=fs得，物体所受斜面的摩擦力：
f=
=
=160N。
5．（2017•烟台）往车上装重物时，常常用长木板搭个斜面，把重物沿斜面推上去，如图所示，工人用3m长的斜面，把120kg的重物提升1m，假设斜面非常光滑，则需要施加的推力为__________，若实质用力为500N，斜面的机械效率为__________，重物遭到的摩擦力为__________。（g取10N/kg）。
【答案】400N；80%；100N。
【分析】（1）斜面非常光滑，故借助功的原理得，人做的有用功等于用斜面所做的功：
W有=Gh=mgh=120kg×10N/kg×1m=1200J；
Fs=mgh=1200J，
解得：
F=
=400N；
（2）人所做的总功：
W总=Fs=500N×3m=1500J；
斜面的机械效率：
η=
×100%=
×100%=80%；
（3）W总=W有+W额
即：Fs=Gh+fs
所以f=
==100N。
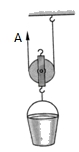
6．（2017•济宁）小可在A端用如图所示的动滑轮匀速提起200N的水桶，若不计绳重、滑轮重及摩擦，则人拉绳子A端的动力为__________N；实质测量A端的拉力为110N，不计绳重及摩擦，则滑轮重为__________N。
【答案】100；20。
【分析】（1）由于动滑轮有两段绳子吊着物体，不计动滑轮重、绳重和摩擦，
拉力F=
G=
×200N=100N；
若不计绳重及摩擦，实质测量A端的拉力为110N时，
依据F=（G+G动）得G动=2F﹣G=2×110N﹣200N=20N。
7.（2019安徽）如图，一轻杆AB悬于O点，其左端挂一重物，右端施加一个与水平方向成30°的力F，此时轻杆水平平衡。若重物水平m＝3kg，BO＝3AO，g取10N/kg。则力F的大小为________N。
【答案】 20
【分析】反向延长力F有哪些用途线，过支点O作力F用途线的垂线即为F的力臂L1 ，
由于右端施加一个与水平方向成30°的力F，则由几何常识可知L1＝ 
OB，
已知BO＝3AO，重物水平m＝3kg，则物体重力G＝mg＝3kg×10N/kg＝30N，
由杠杆平衡条件得：G×L2＝F×L1 ，
即G×OA＝F×OB，
代入数据可得，30N×OA＝F××3OA，
解得F＝20N。
8.（2019安徽）用沿斜面向上大小为3.5N的力将一个重为4.9N的物体从斜面底端匀速拉到顶端。已知斜面长为2m，高为1m，则该过程中斜面的机械效率为________。
【答案】 70%
【分析】用斜面时做的有用功：
W有＝Gh＝4.9N×1m＝4.9J，
拉力所做的功：
W总＝Fs＝3.5N×2m＝7J，
斜面的机械效率：
η＝W有/W总 ×100%＝70%。
9.（2019安徽）如图中物块甲和乙处于静止状况。已知甲重12N，乙重8N，不计绳重及所有摩擦，则甲遭到地面的支持力为________N。
【答案】 4
【分析】物体甲受竖直向下的重力G甲＝12N、竖直向上的拉力F拉＝G乙＝8N、竖直向上的地面的支持力F支用途而静止，处于平衡状况，由力的平衡条件得：G甲＝F拉+F支 ，
则甲遭到地面的支持力：F支＝G甲﹣F拉＝12N﹣8N＝4N。
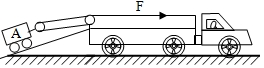
10.（2019四川达州）救援车工作原理如图所示，当车载电机对钢绳施加的拉力F大小为2.5×103N时，小车A恰能匀速缓慢地沿斜面上升。已知小车A的水平为1t，斜面高为2m，斜面长为5m（不计车长、钢绳重、动滑轮重、钢绳与滑轮间的摩擦和滑轮与轴间的摩擦，g＝10Nkg）在小车A由水平路面被拖上救援车的过程中，钢绳所做的有用功为__________J，整个装置的机械效率为__________，小车A与斜面间的摩擦力大小为__________N．
【答案】2×104；80%；1×103。
【分析】（1）小车水平m＝1t＝1000kg，
其重力G＝mg＝1000kg×10N/kg＝1×104N，
钢绳做的有用功：
W有用＝Gh＝1×104N×2m＝2×104J，
（2）不计车长、拉力端移动距离s＝2L＝2×5m＝10m，
拉力做的总功：
W总＝Fs＝2.5×103N×10m＝2.5×104J，
整个装置的机械效率：
η＝＝
×100%＝80%；
（3）不计钢绳重、动滑轮重、钢绳与滑轮间的摩擦和滑轮与轴间的摩擦，克服小车A与斜面间的摩擦做的功为额外功，
W额＝W总﹣W有用＝2.5×104J﹣2×104J＝5×103J，
由W额＝fL可得摩擦力：
f＝
＝
＝1×103N。
11.（2019贵州铜仁） 一电动抽水机10秒内把100kg的水抽到10m高的水池中，则抽水机至少对水做功__________J，在抽水的过程中，若抽水机其消耗的电能是1.25×104J，则抽水机的效率是__________。 解得，L=0.4m
也就是说物体向右运动了1m-0.4m=0.6m W=F·s=4N×0.6m=2.4J
27.（原创题）如图所示，杠杆BC与竖直方向的夹角θ=60°，杠杆BC可以绕B点转动，BC=60cm，在C端遭到水平拉力F有哪些用途，同时C端还和绳子连接，绳子下端系一物体，物体是体积为1dm3，密度为7.8×103 kg/m3的实心金属块，其有1/2部分露出水面时杠杆处于平衡状况。不计杠杆的重力，g=10N／kg。求：
（1）物体的重力G的大小；
（2）物体遭到的浮力的大小；
（3）用途在杠杆C点的水平拉力F的力臂；
（4）用途在杠杆C点的水平拉力F的大小。
【答案】（1）物体的重力G的大小为78N；
（2）物体遭到的浮力的大小为5N；
（3）用途在杠杆C点的水平拉力F的力臂为30cm；
（4）用途在杠杆C点的水平拉力F的大小为73N。
【分析】（1）了解物体的体积和物质密度，应用密度公式ρ=m/v的变形可以求出物体的水平。再依据重力公式G=mg，比较容易求出物体的重力。计算时应该注意单位的统一。
物体的体积v=1dm3=10-3m3
物体的物质密度ρ=7.8×103 kg/m3
依据密度公式ρ=m/v的变形可以求出物体的水平
m=ρV=7.8×103 kg/m3×10-3m3=7.8kg
物体的重力G=mg=7.8kg×10N/kg=78N
（2）依据阿基米德原理的数学表达式F浮=ρ液gV排可以想到，假如液体密度了解、物体排开液体的体积了解，就能求出浮力的大小。
液体是水，水的密度需要记住，ρ水=1.0×103 kg/m3 ， g=10N／kg， V排=v/2=10-3m3/2
则物体遭到的浮力的大小为
F浮=ρ液gV排=1.0×103 kg/m3×10N／kg×10-3m3/2=5N
（3）B点是固定支点，杠杆可以绕它转动。力F有哪些用途线是沿水平方向的，过B点做AC的垂线BD交AC于D，则BD的线段长就是用途在杠杆C点的水平拉力F的力臂。θ=60°
∠BCD=30°，在直角三角形中，30°的角所对的直角边等于斜边的一半，斜边BC=60cm
所以BD=30cm
所以用途在杠杆C点的水平拉力F的力臂大小为30cm。
（4）因为物体在图中状况下处于静止，物体遭到向上的浮力与遭到绳子向上的拉力之和等于物体遭到的竖直向下的重力。即F浮+T=G T=G-F浮
所以杠杆C端遭到绳子竖直向下的拉力F1=T=G-F浮=78N-5N=73N
这个力的力臂依据勾股定理可以得到DC=30cm
依据杠杆平衡条件有：F.BD=F1.DC
F=F1.DC/BD=73N×30cm/30cm=73N
28.（2019天津）用如图所示的滑轮组，将一重为450N的物体以0.1m/s的速度匀速向上提起2m，拉力F为200N．求：
（1）滑轮组的机械效率；
（2）拉力F的功率。
【答案】（1）滑轮组的机械效率为75%；
（2）拉力F的功率为60W。
【分析】（1）工人做的有用功：W有用=Gh=450N×2m=900J，
由图可知，滑轮组绳子的有效股数n=3，拉力端移动距离s=3h=3×2m=6m，
拉力做的总功：W总=Fs=200N×6m=1200J，
滑轮组的机械效率：
η=
×100%=×100%=75%；
（2）由v=得做功时间：
t=
=
=20s，
拉力做功的功率：
P=
=
=60W。
29.（2019广东深圳）如图所示，斜面长s=8m，高h=3m。用平行于斜面F=50N的拉力，将重力为G=100N的物体，由斜面的底端匀速拉到顶端，用时t=10s。求：
（1）有用功W有；
（2）拉力做功的功率 P ；
（3）物体遭到的摩擦力 f ；
（4）该斜面的机械效率h 。
【答案】（1）有用功为 300J；（2）拉力的功率为 40W；
（3）12.5N；（4）斜面的机械效率为 75%．
【分析】（1）有用功为W有=Gh=100N×3m=300J
（2）解：拉力所做的功为W总=Fs=50N×8m=400J
拉力的功率为
（3）额外功为W额=W总−W有=400J−300J=100J
由W额=fs得：
物体遭到的摩擦力
（4）斜面的机械效率为
