(一)求圆锥曲线方程
求圆锥曲线方程分为五个种类,求解方案一般有以下几种:
①几何剖析+方程思想; ②设而不求+韦达定理
 ③概念+数形结合; ④参数法+方程思想
③概念+数形结合; ④参数法+方程思想
种类1——待定系数法
待定系数法本质就是通过对几何特点进行剖析,借助图形,结合圆锥曲线的概念与几何性质,剖析图中已知量与未知量之间的关系,列出含有待定系数的方程,解出待定的系数即可。
 【解法剖析】第Ⅱ小题借助考试试题提供的几何地方关系和数目关系,结合椭圆的几何性质和方程思想,通过待定系数法进行求解。着重考查椭圆的几何性质,将几何特点转化为坐标表示,突显数形结合的思想。
【解法剖析】第Ⅱ小题借助考试试题提供的几何地方关系和数目关系,结合椭圆的几何性质和方程思想,通过待定系数法进行求解。着重考查椭圆的几何性质,将几何特点转化为坐标表示,突显数形结合的思想。

种类2——有关点法求轨迹方程
动点P依靠与另一个动点Q变化而变化,并且动点Q又在另一个已知曲线上,则可先用x,y表示x0,y0,再将x0,y0代入已知曲线,可得到所求动点的轨迹方程。
 【解法剖析】本例第Ⅰ小题充分借助主动点M在椭圆上,而从动点N与主动点M之间存在横坐标相同,纵坐标有 倍的关系,可借助有关点法进行求解。
【解法剖析】本例第Ⅰ小题充分借助主动点M在椭圆上,而从动点N与主动点M之间存在横坐标相同,纵坐标有 倍的关系,可借助有关点法进行求解。
⑴设![]() ,易知
,易知![]()
![]() 又
又![]()
∴![]() ,又
,又![]() 在椭圆上.
在椭圆上.
∴![]() ,即
,即![]() .
.
⑵设点![]() ,
,![]() ,
,![]() ,
,
由已知:![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() .
.
设直线![]() :
:![]() ,
,
由于直线与![]() 垂直.
垂直.
∴![]()
故直线方程为![]() ,
,
令![]() ,得
,得![]() ,
,
![]() ,
,
∴![]() ,
,
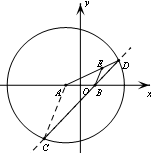 ∵
∵![]() ,
,
∴![]() ,
,
若![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
直线![]() 方程为
方程为![]() ,直线方程为
,直线方程为![]() ,
,
直线过点![]() ,为椭圆
,为椭圆![]() 的左焦点.
的左焦点.
种类3——概念法求轨迹方程
先依据条件确定动点的轨迹是某种已知曲线,再由曲线概念直接写出动点的轨迹方程。

种类4——参数法求曲线方程
当动点P坐标之间的关系较探索时,可考虑x,y之间用同一个变量表示,得到参数方程, 再消去参数即可,但应该注意参数的取值范围。
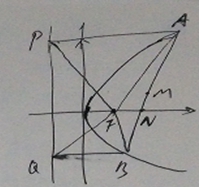
 【解法剖析】本例的第Ⅱ小题以两条直线与抛物线的交点的坐标为参数,借助 面积是 面积的两倍,得到直线AB与x轴交点N的坐标,再进一步借助点差法求得AB中点的轨迹方程。着重考查了设而不求的思想办法。
【解法剖析】本例的第Ⅱ小题以两条直线与抛物线的交点的坐标为参数,借助 面积是 面积的两倍,得到直线AB与x轴交点N的坐标,再进一步借助点差法求得AB中点的轨迹方程。着重考查了设而不求的思想办法。
由AP=AF,BQ=BF及AP//BQ,
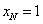
∴AR//FQ.
 设
设![]() ,
,
![]() ,准线为
,准线为![]() ,
,
![]() ,
,
设直线![]() 与
与![]() 轴交点为
轴交点为![]() ,
,
![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,即
,即![]() .
.
设![]() 中点为
中点为![]() ,由
,由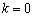 得
得![]() ,
,
又![]() ,
,
∴![]() ,即
,即![]() .
.
∴![]() 中点轨迹方程为
中点轨迹方程为![]() .
.
种类5——直译法求轨迹方程

(Ⅰ)设点![]() ,依题意得
,依题意得![]() ,即
,即![]() ,
,
化简整理得![]() .
.
故点M的轨迹C的方程为![]()
(Ⅱ)在点M的轨迹C中,记![]()
![]() ,
,![]()
![]() .
.
依题意,可设直线![]() 的方程为
的方程为![]()
由方程组![]() 可得
可得![]() ①
①
(1)当![]() 时,此时
时,此时![]() 把
把![]() 代入轨迹C的方程,得
代入轨迹C的方程,得![]() .
.
故此时直线![]() 与轨迹
与轨迹![]() 恰好有一个公共点
恰好有一个公共点![]() .
.
(2)当![]() 时,方程①的辨别式为
时,方程①的辨别式为![]() . ②
. ②
设直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,则
,则
由![]() ,令
,令![]() ,得
,得![]() . ③
. ③
(ⅰ)若![]() 由②③解得
由②③解得![]() ,或
,或![]() .
.
即当![]() 时,直线
时,直线![]() 与
与![]() 没公共点,与
没公共点,与![]() 有一个公共点,
有一个公共点,
故此时直线![]() 与轨迹
与轨迹![]() 恰好有一个公共点.
恰好有一个公共点.
(ⅱ)若![]() 或
或![]() 由②③解得
由②③解得![]() ,或
,或![]() .
.
即当![]() 时,直线
时,直线![]() 与
与![]() 只有一个公共点,与
只有一个公共点,与![]() 有一个公共点.
有一个公共点.
当![]() 时,直线
时,直线![]() 与
与![]() 有两个公共点,与
有两个公共点,与![]() 没公共点.
没公共点.
故当![]() 时,直线
时,直线![]() 与轨迹
与轨迹![]() 恰好有两个公共点.
恰好有两个公共点.
(ⅲ)若![]() 由②③解得
由②③解得![]() ,或
,或![]() .
.
即当![]() 时,直线
时,直线![]() 与
与![]() 有两个公共点,与
有两个公共点,与![]() 有一个公共点,
有一个公共点,
故此时直线![]() 与轨迹
与轨迹![]() 恰好有三个公共点.
恰好有三个公共点.
综合(1)(2)可知,当![]() 时,直线
时,直线![]() 与轨迹
与轨迹![]() 恰好有一个公共点;当
恰好有一个公共点;当![]() 时,直线
时,直线![]() 与轨迹
与轨迹![]() 恰好有两个公共点;当
恰好有两个公共点;当![]() 时,直线
时,直线![]() 与轨迹
与轨迹![]() 恰好有三个公共点.
恰好有三个公共点.
【解法剖析】本题第Ⅰ小题依据题目条件,设出动点的坐标,打造动点M到定点F的距离等于动点到y轴的距离加1的等式,化简求得。当然,本题出可以用概念法进行求解。
(二)求“目的”范围或最值
圆锥曲线中的“目的”取值范围或最值问题,重点是选取适合的变量,打造目的函数,转化为函数的取值范围或最值进行求解。基本方案有:1、几何法。若题目条件和结论明显体现几何特点和意义,则借用图形性质,架构含参数的不等式,通过解不等式得到参数的范围和最值;2、代数法。可从以下五个方面着手:①借助辨别式架构不等式,从而确定参数的取值范围或最值;②借助已知参数的范围确定所求参数的范围,解决这种问题的核心是打造两个参数之间的等量关系;③借助隐含或已知不等关系打造不等式,从而求出参数的取值范围;④借助基本不等式求参数的取值范围;⑤借助函数值域的办法求参数的取值范围。
种类1—角的最值问题
依据三角函数的有关常识可知,求角的取值范围或最值的办法一般是依据条件,将问题转化为求该角的某一个三角函数值,通过求该三角函数值的取值范围,来确定所求角的范围或最值。选择适合的三角函数是解题的重点。







