人教版初二上册数学要点总结
第十二章:全等三角形
12.1全等三角形
(1)、全等图形:形状、大小相同的图形可以完全重合;
(2)、全等形:可以完全重合的两个图形叫做全等形;
(3)、全等三角形:可以完全重合的两个三角形叫做全等三角形;
(4)、平移、翻折、旋转前后的图形全等;
(5)、对应顶点:全等三角形中相互重合的顶点叫做对应顶点;
(6)、对应角:全等三角形中相互重合的角叫做对应角;
(7)、对应边:全等三角形中相互重合的边叫做对应边;
(8)、全等表示办法:用“![]() ”表示,读作“全等于”(注意:记两个三角形全等时,把表示对应顶点的字母写在对应的地方上)
”表示,读作“全等于”(注意:记两个三角形全等时,把表示对应顶点的字母写在对应的地方上)
(9)、全等三角形的性质:①全等三角形的对应边相等;
②全等三角形的对应角相等;
12.2三角形全等的断定
(1)若满足一个条件或两个条件均不可以保证两个三角形肯定全等;
(2)三角形全等的断定:
①三边对应相等的两个三角形全等;(“边边边”或“SS”S)
②两边和它们的夹角对应相等的两个三角形全等;(“边角边”或“SAS”)
③两角和它们的夹边对应相等的两个三角形全等;(“角边角”或“ASA”)
④两角和其中一角的对边对应相等的两个三角形全等;(“角角边”或“AAS”)
⑤斜边和一条直角边对应相等的两个直角三角形全等;(“斜边直角边”或“HL”)
注:①证明三角形全等:判断两个三角形全等的推理过程;
②常常借助证明三角形全等来证明三角形的边或角相等;
③三角形的稳定性:三角形的三边确定了,则这个三角形的形状、大小就确定了;(用“SSS”讲解)
12.3角的平分线的性质
(1)、角的平分线的作法:课本第19页;
(2)、角的平分线的性质定理:角的平分线上的点到角的两边的距离相等;
(3)、证明一个几何中的命题,一般步骤:
①明确命题中的已知和求证;
②依据题意,画出图形,并用数学符号表示已知和求证;
③经过剖析,找出由已知推出求证的渠道,写出证明过程;
(4)、性质定理的逆定理:角的内部到角两边的距离相等的点在角的平分线上;(借助三角形全等来讲解)
(5)、三角形的三条角平分线相交于一点,该点为内心;
复习资料:5.已知△ABC≌△DEF,且∠A=100°,∠E=35°,则∠F=()
A.35° B.45° C.55° D.70°
【考试知识点】全等三角形的性质.菁优网版权所有
6.如图,已知∠ABC=∠DCB,下列所给条件不可以证明△ABC≌△DCB的是()
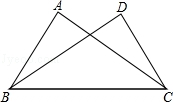
A.∠A=∠D B.AB=DC C.∠ACB=∠DBC D.AC=BD
【考试知识点】全等三角形的断定.菁优网版权所有
7.下列条件中能断定△ABC≌△DEF的是()
A.AB=DE,BC=EF,∠A=∠D B.∠A=∠D,∠B=∠E,∠C=∠F
C.AC=DF,∠B=∠F,AB=DE D.∠B=∠E,∠C=∠F,AC=DF
【考试知识点】全等三角形的断定.菁优网版权所有
8.如图,已知△ABC中,AB=AC,AD=AE,∠BAE=30°,则∠DEC等于()
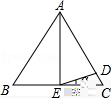
A.7.5° B.10° C.15° D.18°
【考试知识点】等腰三角形的性质;三角形内角和定理;三角形的外角性质.菁优网版权所有
9.如图,A、C、B三点在同一条直线上,△DAC和△EBC都是等边三角形,AE、BD分别与CD、CE交于点M、N,求证:
①△ACE≌△DCB;
②CM=CN.

【考试知识点】全等三角形的断定与性质;等边三角形的性质.菁优网版权所有
10.如图,A、B、C在同一直线上,且△ABD,△BCE都是等边三角形,AE交BD于点M,CD交BE于点N,求证:
(1)∠BDN=∠BAM;
(2)△BMN是等边三角形.

【考试知识点】全等三角形的断定与性质;等边三角形的断定与性质.菁优网版权所有
11.已知:如图,△ABC是等腰直角三角形,D为AB边上的一点,∠ACB=∠DCE=90°,DC=EC.
求证:∠B=∠EAC.
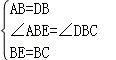
【考试知识点】全等三角形的断定与性质;等腰直角三角形.菁优网版权所有
参考答案与考试试题分析
5.【解答】解:
∵△ABC≌△DEF,
∴∠A=∠D,
∵∠A=100°,
∴∠D=100°,
∵∠E=35°,
∴∠F=180°﹣∠D﹣∠E=45°,
故选B.
6.【解答】解:A、可借助AAS定理断定△ABC≌△DCB,故此选项不合题意;
B、可借助SAS定理断定△ABC≌△DCB,故此选项不合题意;
C、借助ASA断定△ABC≌△DCB,故此选项不符合题意;
D、SSA不可以断定△ABC≌△DCB,故此选项符合题意;
故选:D.
7.【解答】解: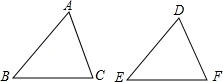
A、依据AB=DE,BC=EF,∠A=∠D,不可以判断△ABC≌△DEF,故本选项错误;
B、依据∠A=∠D,∠B=∠E,∠C=∠F,不可以判断△ABC≌△DEF,故本选项错误;
C、依据AC=DF,∠B=∠F,AB=DE,不可以判断△ABC≌△DEF,故本选项错误;
D、∵在△ABC和△DEF中
 ,
,
∴△ABC≌△DEF(AAS),故本选项正确;
故选D.
8.【解答】解:∵AC=AB,
∴∠B=∠C,
∵∠AEC=∠B+∠BAE=∠B+30°=∠AED+α,
∴∠B=∠C=∠AED+α﹣30°,
∵AE=AD,
∴∠AED=∠ADE=∠C+α,
即∠AED=∠AED+α﹣30°+α,
∴2α=30°,
∴α=15°,
∠DEC=α=15°,
故选C.
9.【解答】证明:①∵△DAC和△EBC都是等边三角形,
∴AC=CD,CE=BC,∠ACD=∠ECB=60°,
∴∠ACE=∠DCB,
在△ACE与△DCB中,
 ,
,
∴△ACE≌△DCB(SAS),
②∵△ACE≌△DCB,
∴∠AEC=∠DBC,
∵∠DCE+∠ACD+∠ECB=180°,∠ACD=∠ECB=60°,
∴∠DCE=∠ECB=60°,
∵CE=BC,∠DCE=∠ECB=60°,∠AEC=∠DBC,
在△EMC与△BNC中,
 ,
,
∴△EMC≌△BNC(ASA),
∴CM=CN.
10.【解答】证明:(1)∵等边△ABD和等边△BCE,
∴AB=DB,BE=BC,∠ABD=∠EBC=60°,
∴∠ABE=∠DBC=120°,
在△ABE和△DBC中,
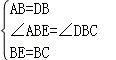 ,
,
∴△ABE≌△DBC(SAS)
∴∠BDN=∠BAM;
(2)∵△ABE≌△DBC,
∴∠AEB=∠DCB,
又∵∠ABD=∠EBC=60°,
∴∠MBE=180°﹣60°﹣60°=60°,
即∠MBE=∠NBC=60°,
在△MBE和△NBC中,
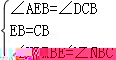 ,
,
∴△MBE≌△NBC(ASA),
∴BM=BN,∠MBE=60°,
∴△BMN为等边三角形.
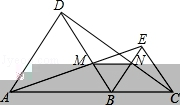
11.【解答】证明:∵△ABC是等腰直角三角形,∠ACB=90°,
∴AC=CB.
∵∠ACB=∠DCE=90°,
∴∠ACE=90°﹣∠ACD=∠DCB.
在△ACE和△BCD中,
 ,
,
∴△ACE≌△BCD(SAS).
∴∠B=∠EAC(全等三角形的对应角相等).






