初中三年级数学要点汇总
二次函数
要点：
1.概念：一般地，假如
是常数，
，那样
叫做
的二次函数.
2.二次函数
的性质
抛物线
的顶点是坐标原点，对称轴是
轴.
函数的图像与
的符号关系.
时
抛物线开口向上顶点为其最低点；
② 当时抛物线开口向下顶点为其最高点
3.二次函数 
的图像是对称轴平行于轴的抛物线.
4.二次函数
用配办法可化成：
的形式，其中
.
5.二次函数由特殊到一般，可分为以下几种形式：
①；②
；③
；④
；⑤.
6.抛物线的五要点：开口方向、对称轴、顶点、与x轴交点、与y轴交点.
① 决定抛物线的开口方向：
当时，开口向上；当
时，开口向下；
相等，抛物线的开口大小、形状相同；越大，开口越小。
②平行于轴的直线记作
.特别地，轴记作直线
.
③求抛物线的顶点、对称轴的办法
公式法：
，∴顶点是，
对称轴是直线
.
配办法：运用配办法将抛物线的分析式化为
的形式，得到顶点为，对称轴是.
运用抛物线的对称性：因为抛物线是以对称轴为轴的轴对称图形，所以对称轴的连线
的垂直平分线是抛物线的对称轴，对称轴与抛物线的交点是顶点.
④抛物线与x轴有无交点的断定状况
⑴
⑵
⑶
⑤抛物线与y轴的交点
★用配办法求得的顶点，再用公式法或对称性进行验证，才能做到万无一失★
9.抛物线中，
有哪些用途
决定开口方向及开口大小，这与中的完全一样.
和一同决定抛物线对称轴的地方.因为抛物线
的对称轴是直线
,故：
①
时，对称轴为轴；②时,对称轴在轴左边；
③时,对称轴在轴右边. （左同右异）
的大小决定抛物线与轴交点的地方.
当时，
，∴抛物线与轴有且只有一个交点：
①
，抛物线经过原点; ②,与轴交于正半轴；③
,与轴交于负半轴.
以上三点中，当结论和条件互换时，仍成立.如抛物线的对称轴在轴右边，则 .
10.几种特殊的二次函数的图像特点如下：
函数分析式 | 开口方向 | 对称轴 | 顶点坐标 |
| 当 开口向上 当 开口向下 |
| |
|
| ||
|
| ||
|
| ||
|
|
11.用待定系数法求二次函数的分析式
一般式：.已知图像上三点或三对、的值，一般选择一般式.
顶点式：.已知图像的顶点或对称轴，一般选择顶点式.
交点式：已知图像与轴的交点坐标、，一般使用交点式：.
12.直线与抛物线的交点
与轴平行的直线与抛物线有且只有一个交点.
平行于轴的直线与抛物线的交点
同一样可能有0个交点、1个交点、2个交点.当有2个交点时，两交点的纵坐标相等，设纵坐标为，则横坐标是的两个实数根.
一次函数
的图像与二次函数的图像
的交点，由方程组
的解的数目来确定：
①方程组有两组不一样的解时与有两个交点;
②方程组只有一组解时与只有一个交点；③方程组无解时与没交点.
抛物线与轴两交点之间的距离：若抛物线与轴两交点为
，因为、是方程的两个根，故 
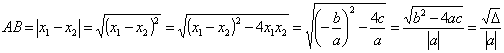
13．二次函数与一元二次方程的关系：
一元二次方程就是二次函数当函数y的值为0时的状况．
二次函数的图象与轴的交点有三种状况：有两个交点、有一个交点、没交点；当二次函数的图象与轴有交点时，交点的横坐标就是当时自变量的值，即一元二次方程
的根．
当二次函数的图象与轴有两个交点时，则一元二次方程有两个不相等的实数根；当二次函数的图象与轴有一个交点时，则一元二次方程有两个相等的实数根；当二次函数的图象与轴没交点时，则一元二次方程没实数根
14、二次函数图象的对称
二次函数图象的对称一般有五种状况，可以用一般式或顶点式表达
1. 关于
轴对称
关于轴对称后，得到的分析式是；
关于轴对称后，得到的分析式是；
2. 关于
轴对称
关于轴对称后，得到的分析式是；
关于轴对称后，得到的分析式是；
3. 关于原点对称
关于原点对称后，得到的分析式是；
关于原点对称后，得到的分析式是；
4. 关于顶点对称（即：抛物线绕顶点旋转180°）
关于顶点对称后，得到的分析式是
；
关于顶点对称后，得到的分析式是
．
5. 关于点对称
关于点对称后，得到的分析式是
依据对称的性质，显然无论作何种对称变换，抛物线的形状肯定不会发生变化，因此永远不变．求抛物线的对称抛物线的表达式时，可以依据题意或便捷运算的原则，选择适合的形式，习惯上是先确定原抛物线（或表达式已知的抛物线）的顶点坐标及开口方向，再确定其对称抛物线的顶点坐标及开口方向，然后再写出其对称抛物线的表达式．
15.二次函数的应用：
二次函数常用来解决最佳化问题，这种问题事实上就是求函数的最大值；
二次函数的应用包含以下方面：剖析和表示不同背景下实质问题中变量之间的二次函数关系；
运用二次函数的常识解决实质问题中的最大值．
15.解决实质问题时的基本思路：理解问题；剖析问题中的变量和常量；用函数表达式表示出它们之间的关系；借助二次函数的有关性质进行求解；检验结果的合理性，对问题加以拓展等．
重难题：
二次函数的图像与性质，二次函数与一元二次方程的关系，用二次函数解决实质问题。
考试知识点：
二次函数在中考中占有非常重要的地位，是中考中的必考内容。中考的主要命题点为：（1）求二次函数的关系式（2）抛物线的顶点、开口方向和对称轴（3）二次函数的最大（小）值（4）抛物线（a≠0）与a,b,c的符号（5）二次函数与一元二次方程（6）二次函数的简单实质问题等。题型主要有选择题、填空题、解答卷，还有探究题和开放题。有关二次函数的热门问题仍然是函数型应用题与方程、几何常识、三角函数等常识综合在一块的综合题、探究题和开放题。
圆的基本性质
要点：
1.圆的有关定义
（1）圆心、半圆、同心圆、等圆、弦与弧。
（2）直径是经过圆心的弦。是圆中最长的弦。弧是圆的一部分。
2.圆周角与圆心角
（1）一条弧所对的圆周角等于它所对的圆心角的一半。
（2）圆周角与半圆或直径：半圆或直径所对的圆周角是直角；
圆周角所对的弦是圆的直径。
（3）圆周角与半圆或等弧：同弧或等弧所对的圆周角相等；
在同圆或等圆中，相等的圆周角所对的弧相等。
3.圆的对称性
（1）圆是中心对称图形，圆心是它的对称中心。
（2）圆的旋转不变性：在同圆或等圆中，假如两个圆心角、两条弧、两条弦中有一组量相等，那样它们所对应的其他各组量分别相等。
（3）圆的轴对称性：经过圆心都的任意一条直线都是它的对称轴。垂径定理是研究有关圆的常识的基础。
垂径定理：垂直于弦的直径平分弦，并且平分弦所对的两条弧。还可以概括为：假如有一条直线,1.垂直于弦；2.经过圆心；3.平分弦（非直径）；4.平分弦所对的优弧；
5.平分弦所对的劣弧，同时拥有其中任意两个条件，那样就能得到其他三个结论。
4.弧长及扇形的面积
弧长公式：
圆弧是圆的一部分，若将圆周分为360份，1°的圆心角所对的弧是圆周长的，由于半径为r的圆周长是2
r，所以n°的圆心角所对的弧长的计算公式为（其中，为弧长，n为弧所对的圆心角度数，r为弧所在圆的半径）
扇形的面积公式：
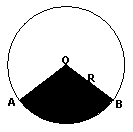1·扇形的概念：一条弧和经过这条弧的端点的两条半径所组成的图形叫做扇形，如图，和半径OA、OB所组成的图形是一个扇形，读作扇形OAB
2·扇形的周长
扇形的周长等于弧长与两半径的长之和，即
3·扇形是圆面的一部分，若将半径为r的圆分为360份，圆心角1°的扇形面积是圆面积的，由于半径为r的圆的面积是
，所以半径为r，圆心角为n°的扇形面积为
4·弧长为，半径为r的扇形面积为
5·扇形面积的应用（求圆的一部分的面积）：
5.圆锥的侧面积和全方位积
圆锥的侧面展开图是一个扇形，如图，设圆锥的母线长为l，底面圆的半径为r，那样这个圆锥的侧面展开图中扇形的半径即为母线长l，扇形的弧长即为底面圆的周长2πr，依据扇形面积公式可知S＝
·2πr·l＝πrl．因此圆锥的侧面积为S侧＝πrl．圆锥的侧面积与底面积之和称为圆锥的全方位积，全方位积为S全=πr2+πrl．
重点：
1.弦和弧的定义、弧的表示办法和点与圆的地方关系。
2.用尺规作图法对不在同一直线上的三个点作圆。
3.垂径定理。（重中之重：“垂直于弦的直径平分弦和弧”常常考）
4.扇形弧长和面积、圆锥侧面积和体积的计算。
难题：
1..对“不在同一直线上的三个点确定一个圆”中的存在性和唯一性的理解
2. 圆锥侧面积计算公式的推导过程需要较强的空间想像能力
3. 类似蚂蚁爬圆锥的计算问题。
4.有关圆的无图多解问题。
考试知识点：
1 垂直于弦的直径
2 圆周角定理及其推论
3 圆内接四边形
4 圆周角、圆心角、弧、弦、弦心距之间的关系
5 圆的性质综合题
相似三角形
要点：
1 相似图形
形状相同的图形叫相似图形，在相似多边形中，最简单的是相似三角形.
2 比率线段的有关定义
假如使用同一单位量得两条线段的长度分别为
，
那样就说这两条线段的比是，或写成．
注意：在求线段比时，线段单位要统一，单位不统一应先化成同一单位．
在四条线段中，假如
的比等于的比，
那样这四条线段叫做成比率线段，简称比率线段．
注意：
当两个比率式的每一项都对应相同，两个比率式才是同一比率式．
比率线段是有顺序的，假如说
是的第四比率项，那样应得比率式为：
．
3 比率的性质
基本性质：
；
．
注意：
由一个比率式只可化成一个等积式，而一个等积式共可化成八个比率式，如，除
了可化为，还可化为，
，，，，
，
．
更比性质：
反比性质：
．
合比性质：
．
注意：事实上，比率的合比性质可扩展为：比率式中等号左右两个比的前项，后项之间
发生同样和差变化比率仍成立．如：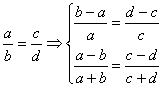
等等．
等比性质：
假如
，那样．
注意：
此性质的证明运用了“设
法” ，这种办法是有关比率计算，变形中一种常用办法．
应用等比性质时，要考虑到分母是不是为零．
可借助分式性质将连等式的每个比的前项与后项同时乘以一个数，再借助等比性质也成立．如：
；其中
．
4 比率线段的有关定理
平行线分线段成比率定理：三条平行线截两条直线，所得的对应线段成比率．
推论：
平行于三角形一边的直线截其它两边所得的对应线段成比率．
平行于三角形一边并且和其它两边相交的直线，所截得的三角形的三边与原三角形三边对应成比率．
定理：假如一条直线截三角形的两边所得的对应线段成比率，
那样这条直线平行于三角形第三边．
5 黄金分割
把线段分成两条线段，且使是的比率中项，叫做把线段黄金分割，点叫做线段的黄金分割点，其中≈0.618．
6 相似三角形的定义
对应角相等，对应边成比率的三角形，叫做相似三角形．
相似用符号“∽”表示，读作“相似于” ．
相似三角形对应边的比叫做相似比．
相似三角形对应角相等，对应边成比率．
注意：
①对应性：即两个三角形相似时，一般把表示对应顶点的字母写在对应地方上，如此写很容易找到相似三角形的对应角和对应边．
②顺序性：相似三角形的相似比是有顺序的．
③两个三角形形状一样，但大小未必一样．
④全等三角形是相似比为1的相似三角形．二者有什么区别在于全等需要对应边相等，而相似需要对应边成比率．
7 相似三角形的基本定理
定理：平行于三角形一边的直线和其它两边相交，所构成的三角形与原
三角形相似．
定理的基本图形：
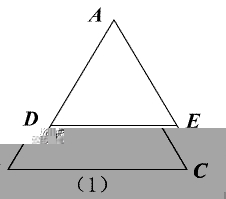
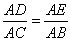
用数学语言表述是：，∽
．
8 相似三角形的等价关系
反身性：对于任一有∽．
对称性：若∽，则∽．
传递性：若∽，且∽，则∽．
9 三角形一样的断定办法
概念法：对应角相等，对应边成比率的两个三角形相似．
平行法：平行于三角形一边的直线和其它两边相交，
所构成的三角形与原三角形相似．
3、断定定理1：假如一个三角形的两个角与另一个三角形的两个角对应相等，那样这两
个三角形相似．简述为：两角对应相等，两三角形相似．
4、断定定理2：假如一个三角形的两条边和另一个三角形的两条边对应成比率，并且夹
角相等，那样这两个三角形相似．简述为：两边对应成比率且夹角相等，两三角形相似．
5、断定定理3：假如一个三角形的三条边与另一个三角形的三条边对应成比率，
那样这两个三角形相似．简述为：三边对应成比率，两三角形相似．
6、断定直角三角形一样的办法：
以上各种断定均适用．
假如一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比率，那样这两个直角三角形相似．
直角三角形被斜边上的高分成的两个直角三角形与原三角形相似．
直角三角形中，斜边上的高是两直角边在斜边上射影的比率中项。每一条直角边是这条直角边在斜边上的射影和斜边的比率中项。
公式 如图，Rt△ABC中，∠BAC=90°，AD是斜边BC上的高，则有射影定理如下：
（1）（AD）2=BD·DC，
（2）（AB）2=BD·BC ，
（3）（AC）2=CD·BC 。
证明：在 △BAD与△ACD中，∠B+∠C=90°，∠DAC+∠C=90°，∴∠B=∠DAC，又∵∠BDA=∠ADC=90°，∴△BAD∽△ACD相似，∴ AD/BD＝CD/AD，即
（AD）2=BD·DC。其余类似可证。
注：由上述射影定理还可以证明勾股定理。由公式（2）+（3）得：
（AB）2+（AC）2=BD·BC+CD·BC =（BD+CD)·BC=（BC）2，
即 （AB）2+（AC）2=（BC）2。
这就是勾股定理的结论。
10 相似三角形性质
相似三角形对应角相等，对应边成比率．
相似三角形对应高的比，对应中线的比和对应角平分线的比都等于相似比．
相似三角形周长的比等于相似比．
相似三角形面积的比等于相似比的平方．
相似三角形性质可用来证明线段成比率、角相等，也可用来计算周长、边长等．
11 相似多边形
假如两个边数相同的多边形的对应角相等，对应边成比率，这两个多边形叫做相似多边形．相似多边形对应边的比叫做相似比．
12 相似多边形的性质
相似多边形周长比，对应付角线的比等于相似比．
相似多边形中对应三角形相似，相似比等于相似多边形的相似比．
相似多边形面积比等于相似比的平方．
注意：相似多边形问题总是要转化成相似三角形问题去解决，因此，熟练学会相似三角形常识是基础和重点．
13 与位似图形有关的定义
1. 假如两个图形不止是相似图形，而且每组对应顶点的连线都交于一点，那样如此的两个图形叫做位似图形.
2. 这个点叫做位似中心，这个时候的相似比又称为位似比.
拓展：
（1） 位似图形是相似图形的特例，位似图形不只相似，而且对应顶点的连线相交于一点.
（2） 位似图形肯定是相似图形，但相似图形可能不是位似图形.
（3） 位似图形的对应边互相平行或共线.
14 位似图形的性质
位似图形上任意一对对应点到位似中心的距离之比等于相似比. 拓展：位似图形有很多性质，它具备相似图形的所有性质.
15 画位似图形
1. 画位似图形的一般步骤：
（1） 确定位似中心
（2） 分别连接原图形中的重点和位似中心，并延长（或截取）.
（3） 依据已知的位似比，确定所画位似图形中重点的地方.
（4） 顺次连结上述得到的重点，即可得到一个放大或缩小的图形.
2. 位似中心的选取：
（1） 位似中心可以在图形外部，此时位似中心在两个图形中间，或在两个图形以外.
（2） 位似中心可取在多边形的一条边上.
（3） 位似中心可取在多边形的某一顶点上.
说明：位似中心的选取决定了位似图形的地方，以上位似中心地方的选取中，每一种办法都能把一个图形放大或缩小.
16 相似三角形容易见到的图形
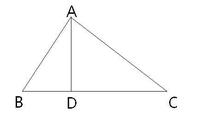
若DE∥BC（A型和X型）则△ADE∽△ABC
射影定理 若CD为Rt△ABC斜边上的高（双直角图形）
则Rt△ABC∽Rt△ACD∽Rt△CBD且AC2=AD·AB，CD2=AD·BD，BC2=BD·AB；
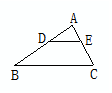
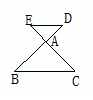
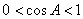
（3）满足1、AC2=AD·AB，2、∠ACD=∠B，3、∠ACB=∠ADC，都可断定△ADC∽△ACB．
（4）当或AD·AB=AC·AE时，△ADE∽△ACB．
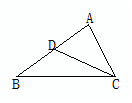
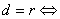
（4）
重点：
相似三角形的断定办法及相似三角形的有关性质
难题：
相似三角形性质的应用
考试知识点：
图形的相似是平面几何中极为要紧的内容。中考的主要命题点为：
比率的性质和黄金分割
相似三角形的概念及相似三角形的断定
相似三角形的性质及其应用
相似多边形的概念和性质
位似图形及其作图等。
题型主要为选择题、填空题、解答卷等，选择题、填空题将重视“相似三角的断定与性质”等入门知识的考查，将在解答卷中加强常识的横向与纵向联系及应用问题的力度。
解直角三角形
要点：
锐角三角函数的概念：
在中，∠C=90°，、、分别是∠A、∠B、∠C的对边，则：
常用变形：；等，由同学们自行总结。
锐角三角函数的有关性质：
当0°<∠A<90°时，
；；；
在0°90°之间，正弦、正切（、）的值，随角度的增大而增大；余弦（）的值，随角度的增大而减小。
同角三角函数的关系：
常用变形： （用概念证明，易得，同学自行完成）
正弦与余弦，正切与余切的转换关系：
如图1，由概念可得： 同理可得：
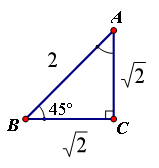特殊角的三角函数值：
三角函数 |
|
|
|
30° |
|
|
|
45° |
|
| 1 |
60° |
|
|
|
解直角三角形的基本种类及其解法总结：
种类 | 已知条件 | 解法 |
两边 | 两直角边 |
|
直角边 |
| |
一边 一锐角 | 直角边 |
|
斜边 |
|
重点：
1、三角函数
特殊角的三角函数值：
| 0° | 30° | 45° | 60° | 90° |
sinα |
|
|
|
|
|
cosplayα |
|
|
|
|
|
tgα |
|
|
|
| / |
互余两角的三角函数关系：sin=cosplayα;…
三角函数值随角度变化的关系
2、解直角三角形
概念：已知边和角（两个，其中必有一边）→所有未知的边和角。
依据：①边的关系：
②角的关系：A+B=90°
③边角关系：三角函数的概念。
注意：尽可能防止用中间数据和除法。
3、对实质问题的处置
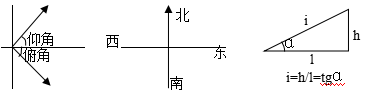俯、仰角： 2．方位角、象限角： 3．坡度：
4．在两个直角三角形中，都缺解直角三角形的条件时，可用列方程的方法解决。
难题：
锐角三角函数的定义
直角三角形的解法
三角函数在解直角三角形中的灵活运用
考试知识点：
1．中考重点考查正弦、余弦的基本定义和求特殊角的三角函数值，及借助正弦和余弦解决一些比较简单的直角三角形问题．
2．中考侧重考查求特殊角的正切值、余切值，借助正切求线段的长．与综合应用三角函数解决测量问题．
3．考查三角形的边角关系是中考容易见到题型，解决此类问题的办法是将一般图形转化为解直角三角形的常识来解决。有时需要添加辅助线．
4．中考中的三角函数与圆的综合题是热门题型．解决这种问题的办法是借助勾股定理、锐
角三角函数关系式．
5．中考解直角三角形应用问题大多是以计算题的形式出现．也是中考的热门题型．
直线与圆，圆与圆的地方关系
要点：
直线与圆有三种地方关系
相交
直线与圆有两个公共点时，大家说直线与圆相交。
相切
直线与圆有唯一的公共点时，大家说直线与圆相切。这条直线叫圆的切线，公共点叫切点。
相离
直线与圆没公共点时，大家说直线与圆相离。
（4） 一般地，直线与圆的地方关系有下面的性质：
若圆的半径为，圆心到直线的距离为，那样
直线与圆相交
直线与圆相切
直线与圆相离
切线的断定与性质
断定定理
经过半径的外端并且垂直这条半径的直线是圆的切线。
性质定理
经过切点的半径垂直于圆的切线。
经过切点垂直于切线的直线必经过圆心。
3. 切线长定理：从圆外一点引圆的两条切线，它们的切线长相等。即如图，AB、AC切圆O于B、C，切线长AB = AC。
4. 弦切角定理：弦切角的度数等于它所夹的弧所对的圆心角度数的一半，等于它所夹的弧所对的圆周角度数（与圆相切的直线，同圆内与圆相交的弦相交所形成的夹角叫做弦切角。）
5.1三角形的内切圆
1． 概念
与三角形三边都相切的圆叫三角形的内切圆，圆心叫三角形的内心，三角形叫圆的外切三角形。
2. 内性情质
内心是三角形角平分线的交点，内心到三角形三边距离相等。
5.2圆与圆的地方关系
1. 相切
（1） 两圆有唯一的公共点时，大家说两圆相切，公共点叫切点。
相切可分为外切与内切
外切：两圆相切，除切点外，一个圆上的点都在另一个圆的外部，大家说两圆外切。
内切：两圆相切，除切点外，一个圆上的点都在另一个圆的内部，大家说两圆内切。
（2） 两圆相切有下面的性质：
若两圆相切，那样切点肯定在连心线上。
设两个圆的半径为
和（），圆心距为，则：
两圆外切
两圆内切
相交
（1） 两圆有两个公共点时，大家说两圆相交。
（2） 性质：相交两圆的连心线垂直平分两圆的公共弦。
相离
两圆没公共点时，大家说两圆相离。
相离可以分为外离与内含。
外离：一个圆上的点都在另一个圆的外部，大家说两圆外离。
内含：一个圆上的点都在另一个圆的内部，大家说两圆内含。
两圆相离有下面的性质：
设两个圆的半径为和，圆心距为，则：
两圆相交
两圆外离
两圆内含
圆幂定理
1、相交线定理：圆内的两条相交弦，被交点分成的两条线段长的积相等。（图一）
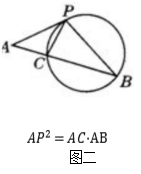
2、切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比率中项。（图二）
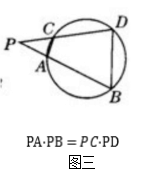
3、割线定理：从圆外一点P引两条割线与圆分别交于A、B；C、D，则有PA·PB=PC·PD（图三）
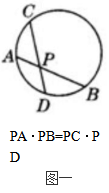
重点：
1.直线与圆、圆与圆地方关系、性质及其断定办法。
2.切线的断定和性质。
3．三角形内心的概念及性质。
难题： 直线与圆、圆与圆的地方关系的断定及应用。
考试知识点： 本章内容是中考的必考内容，主要考查直线与圆、圆与圆地方关系的断定及应用，切线的断定及性质，题型以填空，选择和解答为主，也有开放探索题的新的题型，分值一般在6—10分
