四年级上册要点总结
1、四则运算
1. 加、减法的意义和各部分之间的关系
(1) 加法的意义:把两个数合并成一个数的运算叫做加法。
(2) 加法算式的各部分名字:相加的两个数叫做加数,加得的数叫做和。
(3) 加法各部分间的关系:加数+加数=和,一个加数=和-另一个加数。
(4) 减法的意义:已知两个加数的和与其中的一个加数,求另一个加数的运算叫做减法。
(5) 减法算式的各部分名字:已知的和叫做被减数,已知的一个加数叫做减数,求得的另一个加数叫做差。
(6) 减法各部分间的关系:被减数=差+减数,差=被减数-减数,减数=被减数—差。
(7) 减法是加法的逆运算。
2. 乘、除法的意义和各部分间的关系
(1)乘法的意义:求几个相同加数的和的方便运算叫做乘法。
(2)乘法算式的各部分名字:相乘的两个数叫做因数,乘得的数叫做积。
(3)乘法各部分间的关系:一个因数×一个因数 =积;一个因数=积÷另一个因数。
(4)除法的意义:已知两个因数的积与其中一个因数,求另一个因数的运算叫做除法。
(5)除法算式的各部分名字:已知的积叫做被除数,已知的因数叫做除数,求得的另一个因数叫做商。
(6)除法各部分间的关系:①在没余数的除法中,商=被除数÷除数,除数=被除数÷商,被除数=商×除数。
②在有余数的除法中,被除数=商×除数+余数,商=(被除数-余数)÷除数,除数=(被除数-余数)÷商。
(8) 有关0的运算:a+0= a,a-0= a,a-a = 0,0×a=0,0÷a=0(a≠0)。
(9) 除法是乘法的逆运算。
3.含有括号的四则运算
一个算式里,既有小括号,又有中括号,要先算小括号里面的,再算中括号里面的,最后算中括号外面的。
4.租船问题
解决租船问题的方案:先计算哪种船的租金实惠,再考虑先租这种船,假如这种船没坐满,就进行调整,考虑租另一种船。
【要素提示】
☀在乘法里,0和任何数相乘都得0。
☀1和任何数相乘都得任何数。
☀在除法里,0不可以做除数
2、察看物体(二)
1. 从不同地方察看由小正方体拼摆的物体,辨认察看到的物体的形状的办法:在哪一地方察看物体,就从哪一面数出小正方形的数目,并确定摆出的形状。
2. 从同一地方察看由相同个数的小正方体组成的物体,所看到的平面图形可能相同,也会不相同。
3、运算定律
1. 加法运算定律
(1)加法交换律:两个数相加,交换加数的地方,和不变。用字母表示为a+b=b+a。
(2)加法结合律:三个数相加,先把前两个数相加,或者先把后两个相加,和不变。用字母表示为(a+b)+c=a+(b+c)。
2. 减法的运算性质
(1)一个数连续减去两个数,等于减去这两个数的和。
用字母表示为a-b-c=a-(b+c)。
(2)在连减运算中,任意交换两个减数的地方,差不变。
用字母表示为a-b-c=a-c-b。
3. 乘法运算定律
(1)乘法交换律:两个数相乘,交换两个因数的地方,积不变。
用字母表示为a×b=b×a。
(2)乘法结合律:三个数相乘,先乘前两个数,或者先乘后两个数,积不变。
用字母表示为(a×b)×c=a×(b×c)。
(3)乘法分配律:两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加。用字母表示为(a+b)×c=a×c+b×c或a×(b+c)=a×b+a×c。
4. 除法的运算性质
(1)一个数连续除以两个数,可以用这个数除以两个除数的积。
用字母表示为a÷b÷c=a÷(b×c)(b、c均不为0)。
(2)在连除运算中,任意交换除数的地方,商不变。
用字母表示为a÷b÷c÷d=a÷c÷b÷d(b、c、d均不为0)。
5. 容易见到乘法计算(朋友数字) :25×4=100 125×8=1000
加法交换律简算例子 加法结合律简算例子
75+98+25 488+40+60
=75+25+98 =488+(40+60)
=100+98 =488+100
=198 =588
乘法交换律简算例子 乘法结合律简算例子
25×56×4 99×125×8
=25×4×56 =99×(125×8)
=100×56 =99×1000
=5600 =99000
含有加法交换律与结合律的方便计算 含有乘法交换律与结合律的方便计算
65+28+35+72 25×125×4×8
=(65+35)+(28+72) =(25×4)×(125×8)
=100+100 =100×1000
=200 =100000
6. 乘法分配律简算例子
分解式 合并式
25×(40+4) 135×12—135×2
=25×40+25×4 =135×(12—2)
=1000+100 =135×10
=1100 =1350
特殊1 (添项) 特殊2
99×256+256 45×102
=99×256+256×1 =45×(100+2)
=256×(99+1) =45×100+45×2
=256×100 =4500+90
=25600 =4590
特殊3 特殊4
99×26 35×8—4×35
=(100—1)×26 =35×(8—4)
=100×26—1×26 =35×4
=2600—26 =140
=2574
7. 连续减法方便运算例子
528—65—35 528—89—128 528—(150-128)
=528—(65+35) =528—128—89 =528—128—150
=528—100 =400—89 =400—150
=428 =311 =250
8. 连续除法方便运算例子
3200÷25÷4
=3200÷(25×4)
=3200÷100
=32
9.其他方便运算例子(携带符号搬家)
![]()
![]() 256—58+44 250÷8×4
256—58+44 250÷8×4
![]()
![]() =256+44—58 =250×4÷8
=256+44—58 =250×4÷8
=300—58 =1000÷8
=242 =125
4、小数的意义和性质
1. 小数的意义和读写法
(1)小数的意义:分母是10、100、1000······的分数可以用小数表示。小数的计数单位是十分之1、百分之1、千分之一······分别写作0.1、0.01、0.001······
(2)每相邻两个计数单位间的进率是10。
(3)小数的读法:①先读整数部分,根据整数的读法去读;②再读小数点,小数点读作“点”;③最后读小数部分,依次读出小数部分每个数位上的数。
(4)小数的写法:①先写整数部分,根据整数的写法去写,假如整数部分是零,就直接写“0”;②再在个位的右下角点上小数点;③最后依次写出小数部分每个数位上的数。
小数的数位顺序表
| 整数部分 | 小数点 | 小数部分 | ||||||||||
数位 | … | 万位 | 千位 | 百位 | 十位 | 个位 | · | 十分位 | 百分位 | 千分位 | 万分位 | … | |
计数单位 | … | 万 | 千 | 百 | 十 | 一 | 十分之一 | 百分之一 | 千分之一 | 万分之一 | … | ||
2. 小数的性质和大小比较
(1)小数的性质:小数的末尾添上“0”或去掉“0”,小数的大小不变。
(2)小数大小比较的办法:①先比较整数部分,整数部分大的那个数就大;②整数部分相同,十分位上的数大的那个数就大;③十分位上的数也相同,百分位上的数大的那个数就大······
3. 小数点移动引起小数大小的变化
(1)小数点移动引起小数大小变化的规律:①小数点向右移动一位,小数就扩大到原数的10倍;移动两位,小数就扩大到原数的100倍,移动三位,小数就扩到到原数的1000倍······②反之,小数点向左移动一位,小数就缩小到原来的![]() ;移动两位,小数就缩小到原来的
;移动两位,小数就缩小到原来的![]() ;移动三位,小数就缩小到原来的
;移动三位,小数就缩小到原来的![]() ······
······
(2)小数点移动引起小数大小变化规律的应用:①把一个小数扩大到原来的10倍、100倍、1000倍······就是把这个小数分别乘10、100、1000······也就是把小数点分别向右移动一位、两位、三位·······②把一个小数缩小到原来的![]() 、
、![]() 、
、![]() ······就是把这个小数分别除以10、100、1000······也就是把小数点分别向左移动一位、两位、三位·······
······就是把这个小数分别除以10、100、1000······也就是把小数点分别向左移动一位、两位、三位·······
4. 小数与单位换算
(1)把低级单位的名数改写成高级单位的单位名数的办法:
用这个数除以两个单位间的进率,假如两个单位间的进率是10、100、1000······可以直接把小数点向左移动一位、两位、三位······
(2)把高级单位名数改写成低级单位的单名数的办法:
用这个数乘两个单位间的进率,假如两个单位间的进率是10、100、1000······可以直接把小数点向右移动一位、两位、三位······
水平: 1吨=1000千克 1千克=1000克
长度: 1千米=1000米 1分米=10厘米 1厘米=10毫米
1分米=10厘米 1米=10分米=100厘米=1000毫米
面积: 1平米=100平方分米 1平方分米=100平方厘米
1平方千米=100公顷 1公顷=10000平米
人民币: 1元=10角 1角=10分 1元=100分
5. 小数的近似数
(1)求小数的近似数的办法:
求小数的近似数的办法可以用“四舍五入”法。①当保留整数时,表示精准到个位;②保留一位小数时,表示精准到十分位;③保留两位小数时,表示精准到百分位,精准到哪一位重点看那一位的下一位······
(2)把不是整万数或整亿的数改写成用“万”或“亿”作单位的数的办法:
①先确定万位或亿位,②然后在万位或亿位的右下角点上小数点,③最后在小数的后面写上“万”字或“亿”字,小数的末尾假如有0,要去掉。④改写后还要依据需要保留小数的位数。
5、三角形
1. 三角形的认识及特质
(1)三角形的概念:
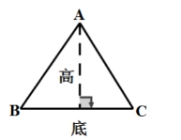
由3条线段围成的图形(每相邻两条线段的端点相连)叫做三角形(如下图),三角形有3条边、3个角和3个顶点。

三角形的高和底:从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫做三角形的高。这条对边叫做三角形的底(如下图)。任意一个三角形都有三条高。(要素提示:三角形的高和底是对应关系)
三角形的特质:三角形具备稳定性。
两点间的距离:两点间所有连线中线段最短,这条线段的长度叫做两点间的距离。
三角形3条边的关系:三角形任意两条边的和大于第三边。
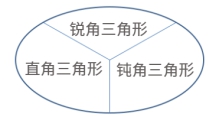
三角形的分类
三角形按角分类:锐角三角形、直角三角形、钝角三角形。3个角都是锐角的三角形叫做锐角三角形。有一个角是直角的三角形叫做直角三角形。有一个角是钝角的三角形叫做钝角三角形。
三角形按边分类:不等边三角形、等腰三角形、等边三角形。
☻等腰三角形:有两条边相等的三角形叫做等腰三角形。在等腰三角形中,相等的两条边叫做腰,两腰的夹角叫做顶角,两腰与底边的夹角叫做底角。等腰三角形的两腰相等,两个底角也相等。
☻等边三角形:3条边都相等的三角形叫做等边三角形(也叫做正三角形)。等边三角形每一个角都是60°。
(3)用集合图表示三角形的分类:

(4)直角三角形:直角三角形中互相垂直的两条边叫做直角边,直角边所对的边叫做斜边。斜边大于任意一条直角边。
3.三角形的内角和
(1)三角形的内角和:三角形的内角和是180°。
(2)三角形内角和的应用:在一个三角形中,已知两个角的度数,求第三个角的度数,用内角和180°连续减去已知的两个角的度数或减去这两个角的度数和。
(3)四边形的内角和是360°。
(4)多边形的内角和=(边数-2)×180°。
6、小数的加法和减法
__________
1.小数加减法
(1)位数相同的小数加减法:
①相同数位对齐,也就是小数点对齐。
②从末位算起,加法应该注意哪一位相加满十,要向前一位进1;减法应该注意哪一位不够减,要以前一位退1当10,在本位上加10再减。
③得数的小数点要与竖式中的小数点对齐。
(2)位数不一样的小数加减法:
①依据小数的基本性质,将位数较少的小数末位添上0,变成位数相同的小数加减法。
②再依据位数相同的小数加减法的计算办法进行计算。
③假如得数的小数部分末尾有0,可以将0去掉。
2.小数加减混合运算的运算顺序
小数加减混合运算的运算顺序,与整数加减混合运算的运算顺序相同。
①没括号的,要按从左到右的顺序进行计算。
②有括号的,先算括号里面的,再算括号外面的。
3.整数加法运算定律推广到小数
(1)整数加法运算推广到小数
在小数加法中,加法交换律和加法结合律同样适用:
☻加法交换律:a+b=b+a
☻加法结合律:(a+b)+c=a+(b+c)。
(2)加法运算定律在小数运算中的应用:
☻减法的性质:a-b-c=a-(b+c)
☻运用“凑整法”解决小数简算的问题。
☻运用找“基准数法”解决小数简算的问题。
7、图形的运动(二)
(一)轴对称
1.轴对称图形的性质
轴对称图形的对称点到对称轴的距离相等。
2.补全轴对称图形的办法
(1)“找”,找出图形上每条线段的端点;
(2)“定”,依据对称轴定每一个端点;
(3)“连”,依次连接这类对称轴,得到轴对称图形的另一半。
(二)平移
1.确定方格中图形平移的方向和距离的办法
(1)依据箭头的指向确定平移的方向;
(2)找出平移前后两个图形的一组对应点,对应点之间的格数就是图形平移的格数。
2.在方格中画简单图形平移后的图形的办法
(1)在原图形上选几个能决定图形形状和大小的点;
(2)按需要把所选的点向规定的方向平移规定的格数;
(3)把平移后的点连点成形。
3.平移的应用
应用图形的平移可以将不规则图形转化成规则图形,进而解决问题。
__________
__________
8、平均数与条形统计图
__________
(一)平均数
1.平均数的意义
一组数据的和除以这组数据的个数,所得的商叫做平均数。它既能够描述一组数据本身的总体状况,也可以作为不同组数据比较的一个标准。
2.求平均数的办法
(1)移多补少法:从多的数目中拿出一部分给少的数目,使它们的数目相等。
(2)公式法:总数目÷总份数=平均数
(二)复式条形统计图
1.绘制纵向复式条形统计图
纵向复式条形统计图的绘制办法与单式条形统计图的绘制办法基本相同,只不过有两组(或多组)数据,需要用两种(或多种)不同颜色(或底纹)的直条来表示,同时要表明图例。
2.依据复式条形统计图进行数据剖析
察看复式条形统计图时,可以运用横向、纵向、综合对比等不一样的办法,从中获得尽量多的信息,而且可以参考获得的信息提出问题并解决问题。
3.绘制复制横向条形统计图
横向复式条形统计图与纵向条形统计图只不过形式上不同,其他都相同。当数据的类型不多,但每类数据又比较大时,用横向复式条形统计图比较便捷。
__________
9、数学广角——鸡兔同笼
1.解题办法
解答“鸡兔同笼”问题可以用列表猜测、假设等多种办法。假设法是假设——计算——推理——解答的过程。当题中所给数据比较大,不容易使用列表猜测法时,用假设法解决问题比较方便。
2.鸡兔同笼问题——假设法
(1)假设全是鸡
兔的只数=(总脚数-鸡的脚数×总只数)÷(兔的脚数-鸡的脚数)
鸡的只数=总只数-兔的只数
(2)假设全是兔
鸡的只数=(兔的脚数×总只数-总脚数)÷(兔的脚数-鸡的脚数)
兔的只数=总只数-鸡的只数