鸡兔同笼问题?看到这个题目,大概有孩子会不屑地说:“小学生都会!”可是今天的问题,不是要解出答案,而是你会用多少种解法解出答案?
不要小看这个“简单”的问题,早在1500年前,《孙子算经》中就记载了这个有趣的问题。WOW,还是个古董呢~
好啦,废话少说,请听题……

题目:现有一笼子,里面有鸡和兔子若干只,数一数,共有头14个,腿38条,球鸡和兔子各有多少只?(请用尽可能多的办法解答)
『 办法1、人见人爱的列表法 』
假如小学二年级小朋友做这道题,可以用列表法!直观、易理解,还困难出错~好啦,大家来看一下!
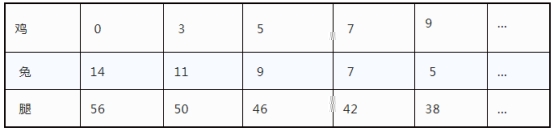
依据上面的表格,大家可以看出,鸡为9只,兔子为5只。大家在列表的时候不要按顺序列,不然做题的速度会非常慢,譬如说列完鸡为0只,兔子为14只,发现腿的数目56条,和实质38条相差较大,那样下一个你可以跳过鸡的数目为2只这样的情况,直接列鸡的数目为3只,如此做速度会快一些哦!
『 办法2、最开心的画图法 』
画图可以让数学变得形象化,而且常常画图还能够帮助创造力的培养!假设14只全部是鸡,先把鸡给画好。
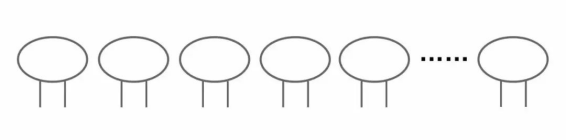
14×2=28条,差38-28=10条,而每一只鸡补2条腿就变成兔子,需要把5只鸡每只补2条腿,所以有5只兔子,14-5=9只鸡。
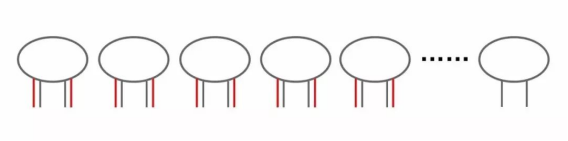
『 办法3、超酷的金鸡独立法 』
剖析:让每只鸡都一只脚站立着,每只兔都用两只后脚站立着,那样地上的总脚数只不过原来的一半,即19只脚。鸡的脚数与头数相同,而兔的脚数是兔的头数的2倍,因此从19里减去头数14,剩下来的就是兔的头数19-14=5只,鸡有14-5=9只。
『 办法4、最逗的吹哨法 』
剖析:假设鸡和兔同意过特种部队练习,吹一声哨,它们抬起一只脚,还有38-14=24只腿在站着,再吹一声哨,它们又抬起一只脚,这个时候鸡都一屁股坐地上了,兔子还有两只脚立着。这个时候还有24-14=10只腿在站着,而这10只腿全部是兔子的,所以兔子有10÷2=5只,鸡有14-5=9只。(惊现跑男中包贝尔的抬脚法有没有!)
『 办法5、最常见的假设法 』
剖析:假设全部是鸡,则有14×2=28条腿,比实质少38-28=10只,一只鸡变成一只兔子腿增加2条,10÷2=5只,所以需要5只鸡变成兔子,即兔子为5只,鸡为14-5=9只。
『 办法6、最常见的假设法 』
剖析:假设全部是兔子,则有14×4=56条腿,比实质多56-38=18只,一只兔子变成一只鸡腿降低2条,18÷2=9只,所以需要9只兔子变成鸡,即鸡为9只,兔子为14 - 9=5只。
『 办法7、最牛的特异功能法 』
剖析:鸡有2条腿,比兔子少2条腿,这不公平,但鸡有2只翅膀,兔子却没。假设鸡有特级功能,把两只翅膀变成2条腿,那样鸡也有4条腿,此时腿的总数是14×4=56条,但事实上只有38条,为何呢?由于大家把鸡的翅膀当作腿来算,所以鸡的翅膀有56-38=18只,鸡有18÷2=9只,兔就是14-9=5只。
『 办法8、最牛的特异功能法2 』
剖析:假设每只鸡兔都具备“ 特异功能 ”,鸡飞起来,兔立起来,这个时候立在地上的脚全是兔的,它的脚数就是38-14×2=10条,因此兔的只数有10÷2=5只,进而了解鸡有14-5=9只。鸡兔具备“特异功能”,这个办法想得太棒了!
『 办法9、最牛的特异功能法3 』
假设孙奥创变成兔子,说“变”,每只兔子又长出一个头来,然后对妖精说“将它劈开”,变成“一头两脚”的两只“半兔”,半兔与鸡都是两只脚,因而共有28÷2=19只鸡兔,19-14=5只,这就是兔子的数目,当然鸡就有14-5=9只。呵呵,小朋友把兔“劈开”成“半兔”,想得奇吧!
『 办法10、最古老的砍足法 』
剖析:倘若把每只砍掉1只脚、每只兔砍掉2只脚,则每只鸡就变成了“独角鸡”,每只兔就变成了“双脚兔”。如此,鸡和兔的脚的总数就由38只变成了19只;假如笼子里有一只兔子,则脚的总数就比头的总数多1。因此,脚的总数19与总头数14的差,就是兔子的只数,即19-14=5(只)。所以,鸡的只数就是14-5=9(只)了。呵呵,这个办法是古人想出来的,但有点残忍!
『 办法十1、史上最坑的耍兔法 』
剖析:倘若刘老师喊口令:“兔子,耍酷!”此时兔子们都把两只前脚高高抬起,两只后脚着地,呈酷酷的姿态,此时鸡兔都是两只脚着地。在地上脚的总数是14×2=28只,而原来有38只脚,多出38-28=10只。为何会多呢?由于兔子们把它们的2只前脚抬了起来,所以兔的只数是10÷2=5只,鸡则是14-5=9只。
『 办法十2、最万能的方程法 』
剖析:设鸡的数目为x只,则兔子有(14-x)只,有2x+4(14-x)=38,解出x=9,所以有鸡9只,兔子14-9=5只。
『 办法十3、最万能的方程法 』
剖析:设兔子的数目为x只,则鸡有(14-x)只,有4x+2(14-x)=38.解得x=5,所以兔子有5只,鸡有14-5=9只。
鸡兔同笼的13种办法就给大伙讲完了,最后大家来总结一下!
• 十三种办法 •
1、列表法2、画图法
3、金鸡独立法4、吹哨法
5、假设法6、假设法
7、特异功能法8、特异功能法
9、特异功能法10、砍足法
11、耍兔法12、方程法
13、方程法
记忆办法:假设“列表”同学画完图将来,有了3大特异功能,摆了一个金鸡独立的pose,吹了一声哨,耍了一下兔,看足了,于是“方程”去了!
声明:图文均源自互联网,侵删








